- •3 Лабораторна робота №3 Дослідження послідовного контура та паралельного контура і виду
- •4 Лабораторна робота №4 Дослідження паралельних контурів другого та третього видів
- •5 Лабораторна робота №5 Дослідження частотних характеристик електричних кіл
- •6 Лабораторна робота №6 Проходження ам – коливань через послідовний коливальний контур
- •7 Лабораторна робота №7 Дослідження пасивних чотириполюсників
- •8 Лабораторна робота №8 Визначення параметрів пасивних чотириполюсників
6 Лабораторна робота №6 Проходження ам – коливань через послідовний коливальний контур
6.1 Мета роботи – дослідження спотворень сигналу, які виникають при проходженні АМ – коливань через одиничний коливальний контур.
6.2 Короткі теоретичні відомості.
Амплітудно-модульованим (АМ) коливанням називається таке коливання, амплітуда якого змінюється в часі за законом керуючого сигналу, що містить інформацію.
Якщо керуючий (модулюючий) сигнал є
гармонічним коливанням з частотою
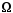 ,
то миттєве значення АМ – коливання може
бути знайдене за виразом:
,
то миттєве значення АМ – коливання може
бути знайдене за виразом:
 ,
(6.1)
,
(6.1)
де
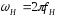 - частота несучого коливання;
- частота несучого коливання;
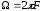 - частота модулюючого коливання;
- частота модулюючого коливання;
Um– амплітуда несучого коливання;
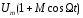 - обвідна амплітуди модульованого
коливання;
- обвідна амплітуди модульованого
коливання;
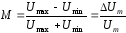 - коефіцієнт глибини модуляції.
- коефіцієнт глибини модуляції.
Значення
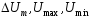 легко визначити з осцилограми АМ –
коливання рис.6.1.
легко визначити з осцилограми АМ –
коливання рис.6.1.
Залежність (6.1) можна подати в вигляді суми гармонічних коливань:
 (6.2)
(6.2)
З формули (6.2) видно, що спектр АМ –
коливання при тональній модуляції
складається з трьох високочастотних
складових (рис.6.2): несучого коливання
з частотою
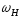 і двох бокових коливань з частотами
і двох бокових коливань з частотами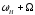 і
і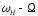 симетрично розміщених відносно частоти
несучого коливання
симетрично розміщених відносно частоти
несучого коливання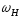 .
Амплітуда бокових складових дорівнюєMUm/2і не перевищує
половини амплітуди несучого коливання
.
Амплітуда бокових складових дорівнюєMUm/2і не перевищує
половини амплітуди несучого коливання
Umax
Um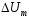
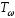


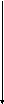

U
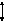

t Umin 

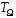

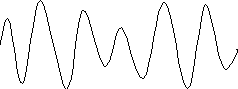
Рисунок 6.1.
Корисна інформація при АМ знаходиться в бокових складових модульованого сигналу.
Розглянемо особливості проходження АМ-сигналу через послідовний коливальний контур.
Нехай АМ-коливання (6.2) з глибиною
модуляції М прикладене до послідовного
контура. Контур налаштований на несучу
частоту АМ-коливання, тобто
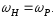
Спектральна діаграма вхідної напруги,
а також частотні залежності модуля
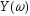 і аргумента
і аргумента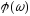 вхідної провідності контура (при умові,
що несуча частота коливання збігається
з резонансною частотою), зображені на
рис.4.2, а і б.
вхідної провідності контура (при умові,
що несуча частота коливання збігається
з резонансною частотою), зображені на
рис.4.2, а і б.
Оскільки контур є системою лінійною,
то струм, що виникає в колі також матиме
три складових з частотами
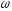 ,
,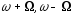 .
Амплітуда струму несучої частоти
дорівнює:
.
Амплітуда струму несучої частоти
дорівнює:
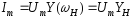 ,
,
а його миттєве значення:
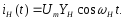 (4.3)
(4.3)
U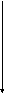
Um
MUm/2 MUm/2
a)

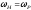
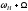

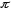 /2
/2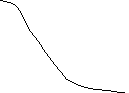

Y
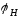
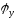
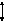
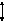


б)
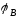
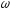

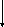

-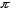 /2
/2
Ya Yb
І Im
в) M’Im/2 M’Im/2
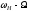
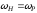
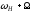

Рисунок 6.2.
Оскільки частотна характеристика
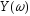 симетрична, то для бокових гармонік
можна записати:
симетрична, то для бокових гармонік
можна записати:
 Іm
верх=Іm ниж=
Іm
верх=Іm ниж=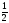 МUmYб,деYб=
МUmYб,деYб=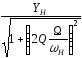 - модуль
- модуль
вхідної провідності при розстроєнні
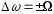 .
.
Фазові зсуви між боковими гармоніками напруги і струму дорівнюють:
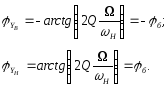
Тому іверх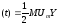 б
б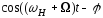 б);
б);
інижн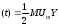 б
б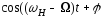 б)
(6.4)
б)
(6.4)
Додавши (6.3) і (6.4), одержимо:
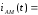
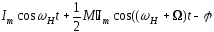 б
б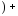
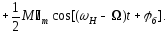 (6.5)
(6.5)
З виразу (6.5), який за формою повністю збігається з (6.2), можна зробити висновок, що обвідна струму, як і обвідна вхідної напруги, змінюється за гармонічним законом.
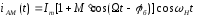 (6.6)
(6.6)
Коефіцієнт
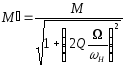 (6.7)
(6.7)
в рівнянні (6.5) відображає глибину
модуляції струму в контурі. З виразу
(6.7) видно, що
 ,
тобто глибина модуляції зменшилась.
Чим вища добротність контура, тим менший
,
тобто глибина модуляції зменшилась.
Чим вища добротність контура, тим менший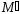 в порівнянні з М.
в порівнянні з М.
Це явище носить назву демодуляції.
З формули (6.6) видно, що обгинаюча струму
зсунута по фазі відносно обгинаючої
напруги на кут
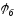 .
Цей зсув зі збільшенням частоти модулюючих
коливань прямує до
.
Цей зсув зі збільшенням частоти модулюючих
коливань прямує до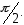
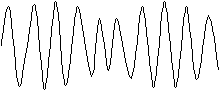
Спектральна діаграма струму в контурі зображена на
рис.6.2, в. Графіки миттєвих значень UAM(t)таіAM(t)приведені на рис.6.3.
UAM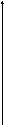



t

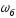
iAM


t

Рисунок 6.3.
Якщо резонансна частота контура не
збігається з несучою частотою (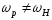 ),
то з’являються спотворення модулюючого
сигналу, викликані порушенням амплітудних
співвідношень між боковими складовими
і складовою несучої частоти (рис.6.4).
),
то з’являються спотворення модулюючого
сигналу, викликані порушенням амплітудних
співвідношень між боковими складовими
і складовою несучої частоти (рис.6.4).
6.2.1 Домашнє завдання.
6.1.1.1 За допомогою моделюючої програми Electronics Workbench (V.5.12.) одержати модель АМ-коливання з М=50% подати його на послідовний контур з параметрами, що вказані на лабораторному макеті, і дослідити вихідний АМ-сигнал при високій і низькій добротності контура (R = 0, R = 39 Ом) при н=р.
6.2.2.2 Те ж саме дослідження зробити при н≠р.
UАМ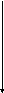
Um
Uниж Uверх
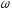

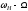
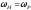
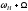

Y
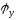
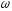

iAM

Iниж
Im
Iверх
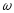
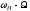
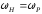


Рисунок 6.4
6.3 Порядок виконання роботи.
6.3.1 Одержати АМ-коливання. Для цього зібрати схему рис.6.5.
Г1Г3
L1 

Г4-102АВ3-38
C1

ГМГМ
Г3-117
Рисунок 6.5.
і подати низькочастотну напругу з виходу генератора Г3-117 на вхід “Внеш. мод.” генератора Г4-102А, встановивши глибину модуляції М=50%, і зарисувати осцилограму.
6.3.2 Подати на вхід контура (рис.6.5) АМ-коливання з несучою частотою, що дорівнює резонансній частоті контура, і модулюючою частотою F, послідовно встановлюючи її значення 1; 5; 10; 15 кГц. Виміряти з екрана осцилографа для кожної модулюючої частоти значення Umaxі Umin, підтримуючи глибину модуляції сигналу на вході контура постійною (М=25-40%).
6.3.3 За одержаними значеннями розрахувати
 для всіх модулюючих частот. Результати
експериментів і розрахунків занести
до табл.6.1.
для всіх модулюючих частот. Результати
експериментів і розрахунків занести
до табл.6.1.
Таблиця 6.1
|
F, кГц |
1 |
5 |
10 |
15 |
|
|
Umax |
|
|
|
|
|
|
Umin |
|
|
|
|
|
|
|
|
|
|
|
|
6.3.4 На одному графіку побудувати
залежність коефіцієнта
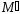 від частоти модуляції
від частоти модуляції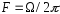 ,
розрахованого з використанням осцилограм
та формули (6.7).
,
розрахованого з використанням осцилограм
та формули (6.7).
6.3.5 Подати на вхід контура АМ-коливання
з несучою
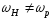 (значення
(значення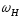 і F задає викладач) від генератора,
встановивши значення М=50%. Зафіксувати
вигляд осцилограми вихідної напруги і
порівняти її з вхідним сигналом.
і F задає викладач) від генератора,
встановивши значення М=50%. Зафіксувати
вигляд осцилограми вихідної напруги і
порівняти її з вхідним сигналом.
6.4 Склад звіту.
1. Короткі теоретичні відомості.
2. Розрахунки і моделі, виконані при підготовці до
роботи.
3. Осцилограми АМ-коливань для різних F.
4. Розрахунки
 різними способами.
різними способами.
5. Схеми дослідів.
6. Таблиці і графіки.
7. Висновки.
6.5Контрольні запитання.
Амплітудна модуляція.
Спектр амплітудно-модульованого коливання при тональній модуляції.
Коефіцієнт глибини модуляції.
Як визначити глибину модуляції АМ-коливання за осцилограмою?
Чим пояснити демодуляцію АМ-коливання при його проходженні через резонансну систему?
Як змінюється вихідний АМ-сигнал при проходженні його через послідовний коливальний контур при
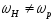 ?
?