11

Лабораторна робота №5

Тема: Побудова найкоротшого шляху у графі

Мета роботи: набути навичок побудови найкоротшого шляху в зваженому графі за допомогою хвильового алгоритму і алгоритму Дейкстри.

Теоретичні відомості:

Хвильовий алгоритм побудови найкоротшого маршруту у незваженому графі

Для незваженого графа довжина маршруту - це число дуг, які вхо­дять в нього. Алгоритм побудови найкоротшого маршруту оснований на покроковому розповсюдженні хвилі від вершини початку маршруту по графу до тих пір, поки хвиля не торкнеться вершини кінця маршруту, і по­тім виділяються дуги, по яким хвиля дійшла до кінцевої вершини.

0. Вершина х_н помічається як 0, а інші вважаються не поміченими; і=0.

1. і=і+1. Помічаються індексом і всі непомічені раніше вершини, в яких є дуги від помічених вершин. Якщо помічена вершина х_к, то виконується п.2, інакше, якщо поточним значенням індексу і виявились поміченими які-небудь вершини, то виконується п.1, інакше робиться висновок, що маршрутів з вершини х_н в вершину х_к немає.

2. Зворотним проходом по дугам, починаючи від вершини х_к, виділяються ті дуги і вершини, які інцидентні виділеним вершинам і різниця між вагами яких рівна 1. Під час руху від вершини х_н по відзначеним дугам виявляються побудовані всі найкоротші маршрути до вершини х_к (рис. 1).

Приклад

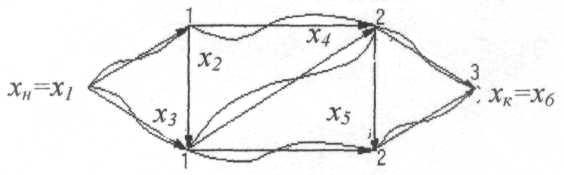
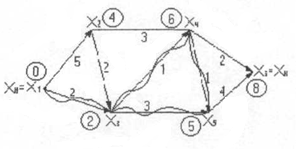
Рис. 1 – Хвильовий алгоритм

Вершина x₁ помічена і=0, вершини х₂ і х₃ помічаються і=1, потім вершини х₄ і х₅ - помічаються і =2, нарешті, вершина х₆=х_к помічається і=3. Зворотній прохід: вершина х₆ виділена, різниці ваг пар вершин х₄,х₆ і x₅,x₆=1, виділяються дуги (х₄,х₆) і (х₅,х₆) і вершини х₄ і х₅. Від цих виділених вершин відповідно їх входам обчислюються різниці ваг пар вершин х₄,х₂, х₄,х₃ і х₅,х₃, які дорівнюють одиниці, і виділяються дуги (х₂,х₄), (хз,х₄) і (х₃,х₅) і вершини х₂ і х₃. Кінцева різниця ваг пар вершин х₂,х₁ і х₃,х₄ дорівнює 1, виділяються дуги (х₁,х₂) і (х₁,х₃). Рухаючись від вершини х₁ по виділеним дугам, отримуємо три найкоротші маршрути:

Довжини l всіх маршрутів однакові і дорівнюють числу і кроків розповсюдження хвилі (l =і=3).

Хвильовий алгоритм для зваженого графа

Відмітимо особливості побудови найкоротшого маршруту для зваженого графа хвильовим алгоритмом.

1. Замість одиничної зміни індекса і (номера кроків розповсюдження

хвилі) під час обчислення пройденого маршруту для кожної вершини по­винна використовуватися сума ваг l_і,j дуг (x_i,x_j), які ведуть до цієї вершини від вершини х_н. До кожної вершини можуть йти від вершини х_н декілька маршрутів, суми довжин дуг по різних маршрутам відмінні. Під час пошуку найкоротшого маршруту необхідно вибирати найменшу суму. Хвилі розповсюдження ваги по різним маршрутам доходять до кожної вершини послідовно, при черговій хвилі необхідно або залишити стару вагу вершини, або замінити її на новий (менший). Тому під час розрахунку ваги вершини х_і за рахунок хвилі, що дійшла до неї дузі (x_j,x_i), обчислення ваги V_i визначається за формулою V_i= min(V_i ,V_j+l_y).

2. Ваги вершин в процесі розповсюдження хвилі можуть змінюватися

неодноразово. При кожній зміні ваги V_i вершини це зменшення необ­хідно передати вершинам виходу х_і тобто необхідні спеціальні засоби, які відображують факти отримання вершиною нової ваги і передачу її іншим вершинам. В якості такого засобу використовуються масиви номерів вер­шин, які отримали нову вагу (при кожній зміні ваг номерів вершини вклю­чаються у цей масив, якщо його там не було при передачі ваги - виключається).

Приклад

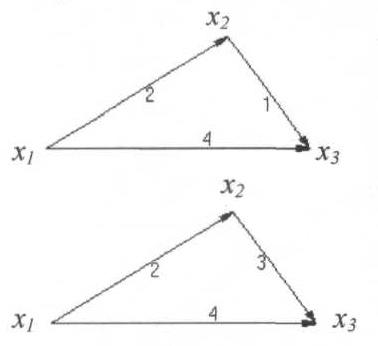
Крок 0: V₁=0.

Крок 1: V₂=0+2=2,

V₃=0+4=4

Крок 2: V₃=min(4,2+1)=3

Крок 0: V₁=0.

Крок 1: V₂=0+2=2,

V₃=0+4=4

Крок 2: V₃=min(4,2+3)=4

Формулювання алгоритму.

1. Вершина х_н отримує вагу V_H=0, її номер вводиться в масив М но­мерів вершин, які змінили вагу. Всі інші вершини, що залишилися, x_i отри­мують вагу V_i= і їх номери не попадають в масив М.

2. Якщо масив М порожній, то виконується п.3, інакше вибирається з виключенням з нього чергової вершини x_i і перераховуються ваги вершин, які належать виходу G(x_i)(V_j=min(V_j,V_i+l_ij)). Якщо вага V_j зменшується, то номер j включається зі зведенням подібних в М. Знову виконується п.2.

3. Якщо вага V_K=, то робиться висновок, що маршрутів з вершини х_н до вершини х_к нема, інакше виконується процедура виділення дуг, така ж, як і в хвильовому алгоритмі для незваженого графа, за виключенням, що різниця ваг вершин x_i і x_lj повинні бути рівні l_ij. Після виділення дуг буду­ються найкоротші маршрути, довжини яких дорівнюють V_K.

Приклад

Розглянемо граф зображений на рис. 2.

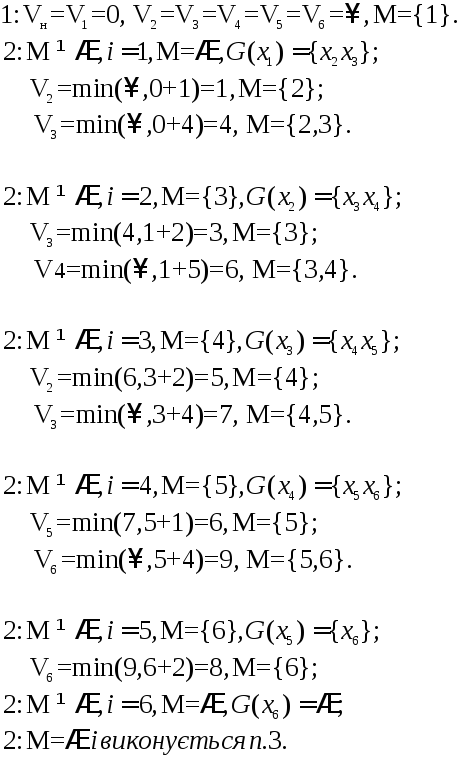
Починаємо з вершини х₆. G^-1(x₆)={x₄,x₅}; (l_4,6=4)(V₆-V₄=3), тому дуга (х₄,х₆) не виділяється. (l_5,6=2)=(V₆ -V₅=2) і дуга (х₅,х₆) виділяється, одно­часно виділяється вершина х₅. Для виділеної вершини х₅: G^-1(x₅)={x₃,x₄}; (l_3,5=4)(V₅ – V₃=3), дуга (х₃,х₅) не виділяється; (l_4,5=1)=(V₅-V₄=1), виділені дуга (х₄,х₅) і вершина х₄. Для вершини х₄: G^-1(x₄)={x₂,x₃}; (l_2,4=5)(V₄-V₂=4), дуга (х₂,х₄) не виділяється; (l_3,4=2)=(V₄-V₃=2), виділяється дуга(х₃,х₄) і вершина х₃. Для вершини х₃: G^-1(x₃)={x₁,x₂}; (l_1,3=4)(V₃-V₁=3), то­му дуга (х₁,х₃) не виділяється; (l_2,3=2)=(V₃ -V₂=2) і дуга (х₂,х₃) виділяється, одночасно виділяється вершина х₄. G^-1(x₂)={x₁};(l_1,2=1)=(V₂–V₁=1), виді­ляється дуга (х₁,х₂).Побудований найкорот-ший маршрут (х_н,х_к) довжиною 8. (х_н=х₁,х₂)(х₂,х₃)(х₃,х₄)(х₄,х₅)(х₅,х₆=х_к).

Процес розв'язання можна офор­мити у вигляді такої таблиці:

X1	X2	X3	X4	X5	X6	M
0	∞	∞	∞	∞	∞	1
0	1	4	∞	∞	∞	2,3
0	1	3	6	∞	∞	3,4
0	1	3	5	7	∞	4,5
0	1	3	5	6	9	5,6
0	1	3	5	6	8	6
0	1	2	5	6	8

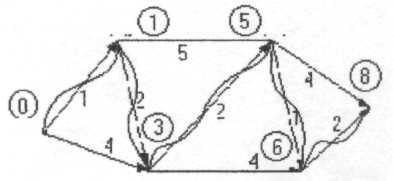
Наведемо ще один приклад (рис. 3) з коротким записом процесу розв'язання

X1	X2	X3	X4	X5	X6	M	Рисунок 3
0	∞	∞	∞	∞	∞	1
0	5	2	∞	∞	∞	2,3
0	5	2	8	6	∞	3,4,5
0	4	2	8	5	∞	4,5,2
0	4	2	8	5	10	5,2,6
0	4	2	6	5	9	2,6,4
0	4	2	6	5	9	6,4
0	4	2	6	5	9	4
0	4	2	6	5	8	4
0	4	2	6	5	8

На наведеному графі відмітимо вершини отриманими числовими значеннями ваг і виділимо найкоротші маршрути. Отримано два найкоротших маршрути довжиною 8: