Lab6_descreet_math.doc

4

Лабораторна робота №6

Тема: Побудова стовбура графа

Мета роботи: набути навичок побудови стовбура графа.

Теоретичні відомості:

2.4.2. Дерево, стовбур графа.

Визначення дерева. Кінцевий зв’язний граф без циклів називається деревом. З властивостей відсутності циклів і зв’язності випливає, що р=1 і =0=m-n+1; число ребер в дереві на одиницю менше числа вершин. Ми вже зустрічалися з поняттям дерева, коли фіксували процес вирішення в задачі про покриття у вигляді дерева. Приклади графів-дерев показані на рис.2.23.

Н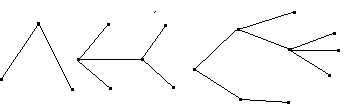агадаємо, що вершини дерева, яким інцидентне лише одне ребро, називається листками (висячими вершинами). Одна з вершин може бути оголошена коренем дерева.

Теорема 2.3. Існує D_n=n^n-2 різних дерев на n вершинах.

Доведення зводиться до двох конструктивних побудовах, приведення дерева до набору номерів вершин і, навпаки, відновлення по цьому набору дерева. Однозначність процесу дозволяє припустити, що число дерев дорівнює числу наборів і таким чином розрахувати число дерев, уточнивши властивості наборів. Процес побудови набора по дереву.

1. Розглядаємо дерево з n2 вершинами. Вихідний набір пустий.

2. Якщо перетворюване дерево зберегло лише дві вершини, то процес закінчений, інакше знаходимо серед листків вершину з найменшим номером. Цю вершину виключаємо з дерева разом з інцидентним їй ребром, в набір включаємо номер вершини, з якою з’єднана вершина, що видаляється. Знову виконуємо п.2.

Н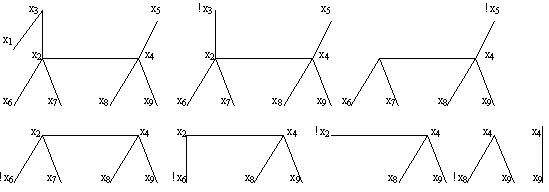а рис. 2.24 зображена вся послідовність побудови набору А і перетворення дерева. Знаком оклику відмічена вершина, яка обирається з найменшим номером.

Сформулюємо процес відновлення дерева по набору А:

1. Будуємо набір В, рівний послідовності номерів вершин в порядку збільшення: В=(1,2,...n).

2. Якщо в наборі В залишилось всього два номери вершин, то з’єднаємо їх і шукане дерево побудовано, інакше знаходимо в В мінімальний номер, якого немає в наборі А, і з’єднуємо цю вершину з вершиною , номер якої вказаний першим в наборі А. Викреслюємо ці номера з А і В.

Знову виконуємо п.2. Для даного прикладу процес показаний на рис.2.25.

О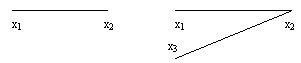тже, з наведеного прикладу видно, що процес побудови набора А і відновлення дерева однозначний. Набір А – це розміщення (важливий порядок) з повтореннями. Довжина набору рівна n-2.

Звідси D_n=n^n-2. Формула доведена.

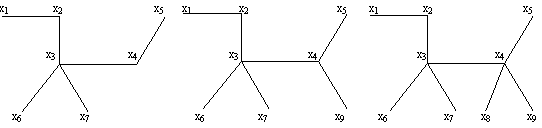
А=(3, 2, 4, 2, 2, 4, 4) А=(2, 4, 2, 2, 4, 4)

В=(1, 2, 3, 4, 5, 6, 7, 8, 9) В=(2, 3, 4, 5, 6, 7, 8, 9)

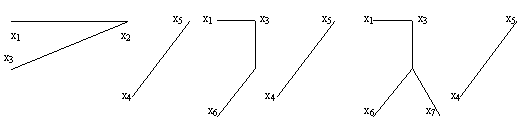
рис.2.25

А=(4, 2, 2, 4, 4) А=(2, 2, 4, 4) А=(2, 4, 4)

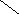
В=(2, 4, 5, 6, 7, 8, 9) В=(2, 4, 6, 7, 8, 9) В=(2, 4, 7, 8, 9)

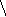А=(4, 4) А=(4) А=

В=(2, 4, 8, 9) В=(4, 8, 9) В=(4, 9)

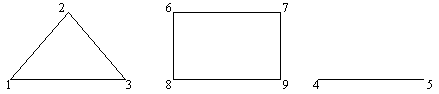
В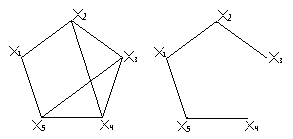изначення стовбура графа. Якщо граф не зв’язаний, то розглядаємо його окремі компоненти. Стовбур такого графа визначений як сукупність стовбурів його компонент. Для кожної компоненти частковий підграф, який може бути побудований з неї видаленням деяких ребер і який є деревом, називається стовбуром. В загальному випадку для графа можна побудувати декілька стовбурів. Для даного прикладу (рис.2.26).

Один з можливих стовбурів для незв’язного графа показаний на рис.2.27.

Алгоритм побудови довільного стовбура.

1.Для кожної компоненти і графа виконуємо п.2 і 3.

2.Будуємо частинний граф, який має всі n_і вершин компоненти і не маючий ребер ( граф).

3.Якщо в поточний частинний граф включені уже n_і-1 ребер, то стовбур для компоненти і побудований, інакше вибираємо наступне нерозглянуте ребро компоненти і намагаємось його включити в поточний граф. Якщо в поточному графі це не приводить до створення циклу, то включаємо ребра, інакше – не включаємо. Ребро вважається розглянутим. Виконуємо п.3.

Приклад для графа показаний на рис.2.17. В ньому тільки одна компонента. На рис.2.28 зображена послідовність включення ребер в порядку їх нумерації на рис.2.19.

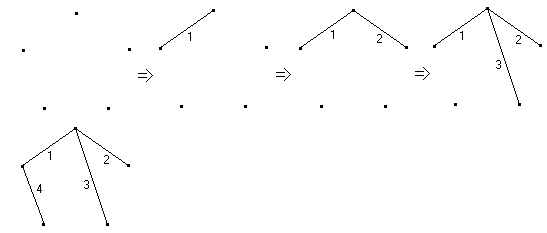
рис.2.28.

Оскільки цикл не створився, то всі ребра з номерами 1,2,3,4 включені в стовбур і так як m=n-1, то стовбур побудований.

Якщо вибрати другу послідовність перегляду ребер для включення в стовбур (наприклад, 5,6,7,2,3,1,4), то не всі розглянуті ребра будуть включені в стовбур, тому будується другий стовбур (рис.2.29).

Визначення і алгоритм побудови мінімального стовбура. Для зваженого графа стовбур з найменшою сумою ваг ребер, які в нього ввійшли, називається мінімальним (найкоротший зв’язковий стовбур). В 2.3 обґрунтовано, що при розгляді ребер в сформульованому раніше алгоритмі побудови звичайного стовбура в порядку зростання їх ваг буде побудований мінімальний стовбур. Наприклад, якщо ваги ребер відповідають їх нумерації на рис.2.19, то на рис.2.28 побудований мінімальний стовбур. Для графа (див.рис.2.17) з другими вагами мінімальний стовбур побудований на рис.2.30.

Задача про мінімальний стовбур має очевидні інтерпретації: ℓ_іj – довжина, тоді маємо найкоротший зв’язок всіх вершин; ℓ_іj – ціна, самий дешевий зв’язок всіх вершин, тощо.

Порядок виконання роботи:

1. Проаналізувати метод побудови стовбура графа на конкретному прикладі згідно з індивідуальним завданням.

2. Розробити схему алгоритму побудови стовбура графа.

3. Розробити програму, яка реалізує даний алгоритм.

4. Для заданого варіанту привести результати тестування розробленої програми.

5. Розробити інструкцію користувача.

6. Оформити звіт і зробити висновки за результатами роботи.

Б. Побудувати найменший стовбур для графів завдання підрозділу 3.2.1, якщо ваги ребер беруться як ваги ребер наступного повного графа (рис.2.33).

Варіанти завдань див. лаб. 9-10.