3 Лабораторна робота №3 Дослідження послідовного контура та паралельного контура і виду

3.1 Мета роботи – дослідити резонансні явища та визначити основні параметри послідовного контура та паралельного контура першого виду

3.2 Короткі теоретичні відомості

Резонансні явища мають велике значення в радіотехніці, оскільки на них грунтується робота більшості радіотехнічних пристроїв.

Резонансом називають таке явище в електричному колі, що має індуктивності і ємності, коли частота власних коливань кола збігається з частотою коливань генератора.

Еквівалентний реактивний опір чи реактивна провідність кола, де є резонанс, дорівнюють нулю.

3.2.1 Послідовний коливальний контур (рис.3.1).

Вхідний комплексний опір послідовного коливального контура: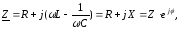(3.1)

де 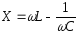- реактивний опір контура;

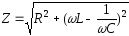- повний опір контура;

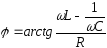- фазовий зсув між напругою і струмом.

U_L

R L

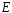C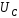

Рисунок 3.1

При Х_L=X_C в послідовному коливальному контурі виникає резонанс напруг.

Кутова резонансна частота

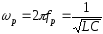(3.2)

При резонансі напруг використовуються такі співвідношення та формули:

а) характеристичний опір контура – опір кожного з реактивних елементів при резонансі

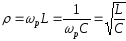, (3.3)

б) добротність контура

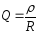, (3.4)

в) згасання контура

. (3.5)

При резонансі напруг струм в контурі

,

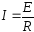а напруга на індуктивності дорівнює напрузі на ємності і в добротність раз більша напруги генератора

.

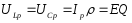Розстроювання:

- абсолютне - 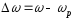або;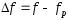

- відносне - ;

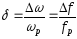- узагальнене .

Відношення комплексного опору до резонансного опору контура

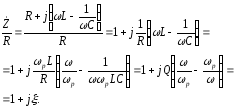
Модуль цього виразу

(3.7)

Фазовий зсув

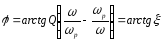, (3.8)

Відношення комплексного струму в контурі до його резонансного значення

(3.9)

Частотна залежність модуля цього відношення

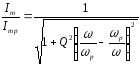(3.10)

називається амплітудно-частотною характеристикою.

Рівняння фазочастотної характеристики

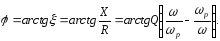(3.11)

При невеликих розстроюваннях

при цьому вирази (3.7), (3.10), (3.11) приймають такий вигляд:

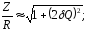
.(3.12)

Смуга пропускання визначається при умові, що струм на частотах f_ніf_в, які відповідають межі смуги пропускання, зменшується відносно резонансного в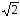раз (рис. 3.2), що дорівнює 3 дБ.

I_m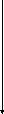

І_mp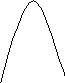

ff

f_нf_pf_вf

Рисунок 3.2.

Абсолютне та відносне значення смуги пропускання визначають з допомогою формул:

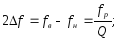
Звідси добротність коливального контура

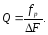(3.13)

3.2.2 Паралельний коливальний контур першого виду (рис. 3.3).

Паралельним коливальним контуром називають таке електричне коло, в якому джерело енергії, індуктивність і ємність з’єднані паралельно. В такому електричному колі може відбуватись резонанс струмів.

Комплексна провідність кола:

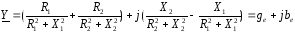(3.14)

В момент резонансу

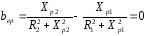. (3.15)

Умова резонансу

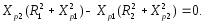(3.16)

З умови резонансу визначається резонансна частота:

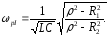(3.17)

І

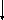
І₁ I₂

R_iR₁ R₂

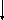
e (t)

C

L

Рисунок 3.3.

З виразу (3.15) знаходимо:

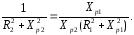(3.18)

З врахуванням (3.18) знаходимо резонансну провідність контура першого виду:

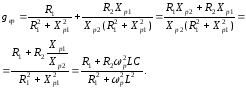
Опір паралельного контура в момент резонансу

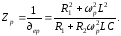(3.19)

Добротність контура

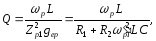(3.20)

де 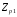- модуль резонансного опору індуктивної гілки;

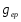- резонансна провідність контура.

Струм в нерозгалуженій частині кола при резонансі

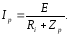
Окремі випадки резонансу струмів для кола (рис. 3.3):

а) коло не має втрат (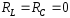). Умова резонансу

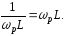
Кутова резонансна частота

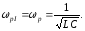
Резонансний опір контура без втрат .

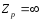б) коло має незначні втрати, тобто 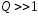.При незначних втратах можна вважати, що

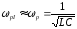
Опір такого контура при резонансі

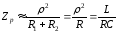, (3.21)

де

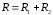
в) втрати в ємнісній і індуктивній гілках контура однакові, тобто 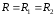. При цьому резонансна частота:

,

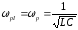а резонансний опір:

.

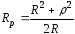Для більшості контурів можна приймати 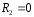, тоді приходимо до окремого випадку контура першого виду (рис.3.4).

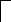
R

С

L

Рисунок 3.4.

Резонансна частота такого контура:

,

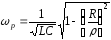а добротність на підставі (3.16)

.

Резонансний опір в відповідності з (3.19)

.

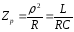Струми в кожній з гілок при резонансі приблизно однакові і утворюють так званий контурний струм:

,

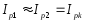При цьому виконується умова:

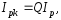
що відображає співвідношення контурного струму і струму в нерозгалуженій частині кола.

При під’єднанні до паралельного контура джерела ЕРС Ез внутрішнім опоромR_i струм в нерозгалуженій частині і напруга

на контурі при будь-якій частоті визначають за формулами:

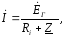
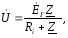
а при резонансі

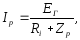
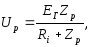
Відношення цих напруг

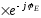, (3.22)

де еквівалентна (приведена) добротність

,

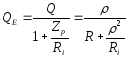а кут зсуву фаз напруги на контурі при будь-якій частоті до цієї напруги при резонансі

.

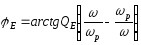3.3 Порядок виконання роботи.

3.3.1 Послідовний коливальний контур.

3.3.1.1 Під’єднати до клем Г₁та Г_м(рис.3.5) генератор сигналів Г3-117, а до клем Г₃та Г_м– вольтметр. Змінюючи частоту на виході генератора, досягнути резонансу в досліджуваному контурі. Порівняти значення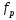з розрахованим в домашньому завданні.

3.3.1.2 Виміряти напругу на конденсаторі U_C (клеми Г₃- Г_м) при резонансі і на вході коливального контураU_Г(клеми Г₂- Г_м). Для цього на вході подати напругу від генератора Г3-117 на клеми Г₁та Г_м. Знайти добротність як відношення цих напруг

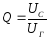
та порівняти знайдене значення з результатом, одержаним для добротності в п.3.3.1.4.

3.3.1.3 Одержати резонансну криву досліджуваного контура 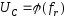, змінюючи частоту генератора через 1-2 кГц і вимірюючи напругуU_C.

Напругу U_Гпідтримувати постійною.

SA

R₁Г₃R₅

39SA₁200к

Г₁

R₃

Г₂ 39 Г₁Г₃

R₂ C R₄

1 1нФ 20 к

L C

2,5 мГн 1нФ

Г_МГ_М Г_М Г_М

а) б)

Рисунок 3.5.

Ввімкнути в контур додатковий резистор R₃ і ще раз зняти резонансну криву.

При одержанні резонансних кривих обов’язково користуватись ручкою плавного перестроювання.

Результати вимірів занести в табл.3.1.

Таблиця 3.1.

fГ, кГц,											Примітка
UC, В											UГ=;
											UГ=;

3.3.1.4 Побудувати резонансні криві за п.3.3.1.3 на одному графіку і визначити по них смугу пропускання 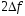, добротністьQ, індуктивність котушкиL та хвильовий опір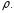

3.3.2 Паралельний коливальний контур.

3.3.2.1 Під’єднати генератор до клем Г₁, Г_м (рис.3.5), а вольтметр – до Г₃, Г_м.

Перемикачем SA₁ввімкнути опір R_5.. Змінюючи частоту генератора, досягнути резонансу в досліджуваному контурі на резонансній частоті. Порівняти її з розрахованою.

3.3.2.2 Зняти і побудувати резонансну криву . Результати записати в табл.3.2.

Таблиця 3.2.

f, кГц,											Примітка
U, В											UГ=;R5=
											UГ=; R4=

3.3.2.3 Ввімкнути опір R₄. Зняти і побудувати резонансну криву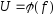. Результати занести до табл.3.2. По резонансній кривій визначити добротність контураQ.

3.4 Домашнє завдання.

3.4.1 З допомогою моделюючої програми Electronics Workbench (v.5.12.) за даними рис. 3.5 змоделювати амплітудно-частотні характеристики послідовного контура та паралельного контура першого виду.

3.4.2 Розрахувати резонансні частоти послідовного та паралельного контурів за виразами (3.2) і (3.17).

3.5 Склад звіту:

• короткі теоретичні відомості;

• розрахунки, виконані при підготовці до заняття;

• резонансні криві, одержані в домашньому завданні і в процесі роботи;

• таблиці з експериментальними даними;

• розрахунки параметрів контурів, які необхідно провести в ході виконання роботи;

• досліджувані схеми;

• аналіз одержаних результатів.

3.6 Контрольні запитання.

1.Чому резонанс в послідовному контурі називається резонансом напруг?

2. Параметри, що характеризують послідовний контур, їх значення.

3. Яку залежність називають амплітудно-частотною характеристикою послідовного контура?

4. При якій умові реактивний опір послідовного контура має індуктивний характер, а при якій - ємнісний?

5. Як визначити смугу пропускання контура?

6. Як по резонансній кривій визначити добротність контура і опір втрат?

7. Резонанс струмів.

8. Коли еквівалентний опір паралельного контура приймає індуктивний, а коли ємнісний характер?

9. Фазо-частотна характеристика контура.

10. Параметри контура при малих розстроюваннях.

11. Окремі випадки контура І виду.

12. Як впливає на добротність контура І виду внутрішній

опір генератора?

13. Як взаємозв’язані добротність і смуга пропускання

контура?

14. Як змінюється резонасне значення напруги на

паралельному контурі І виду від зміни внутрішнього

опрору генератора?