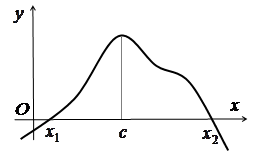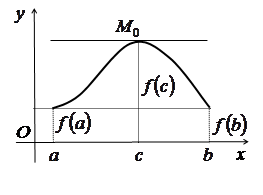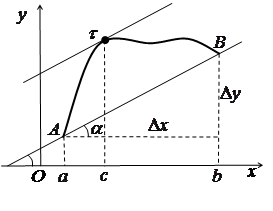3.4 Похідні та диференціали вищих порядків

(higher derivative, higher-order differential)

 

Нехай функція диференційовна на проміжкуX, а  її похідна, яка також є функцією відносно x. Від цієї функції знову можна шукати похідну за умови, що вона існує на заданому проміжку. Похідна від похідної називаєтьсяпохідною другого порядку (second-order derivative) функції і позначається одним із символів:

 

.

 

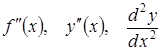Так у фізиці, якщо  закон, за яким змінюється пройдений шлях при прямолінійному русі точки, то єприскоренням (acceleration) цієї точки в момент часу t.

 

Аналогічно і т. д.

 

Взагалі похідною n-го порядку від функції називається похідна від похідної-го порядку і позначається

 

, або , або.

 

Зауваження. При , похіднуn-го порядку позначають відповідно ; припозначають:або.

Приклад 3.17. Знайти похідну другого порядку від функції

 

.

Розв’язання. Знаходимо спочатку за формулою.

 

 

.

 

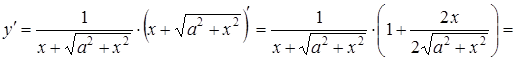
Знаходимо похідну від отриманої функції:

 

 

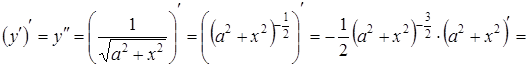
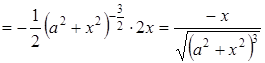, тобто .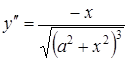

 

 

Приклад 3.18. Знайти похідну n-го порядку від функції .

Розв’язання.

.

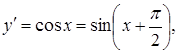
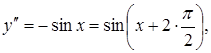
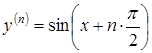Формула Лейбніца. Якщо функції ,мають похідні доn-го порядку включно, то для обчислення похідної n-го порядку від добутку цих функцій використовують формулу Лейбніца:

.         (3.14)

 

Похідні вищих порядків від функцій, заданих параметрично. Якщо функції іпараметрично задають функцію, то похідні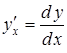,,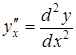 можна послідовно обчислити за формулами:

 

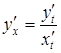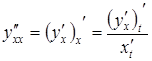,  і т. д.

 

Так, для похідної другого порядку має місце формула:

 

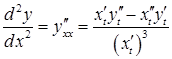.                               (3.15)

 

Приклад 3.19. Знайти похідну функції, заданої параметрично:,.

Розв’язання.

 

.

 

за формулою (3.15)

 

.

 

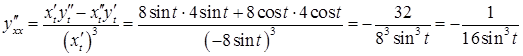Диференціали вищих порядків. Нехай функція диференційовна на проміжкуX. Її диференціал

 

 

називається також диференціалом першого порядку і його можна розглядати як функцію змінної x(приріст аргументу вважається сталим).

Означення 3.4. Диференціалом другого порядку (second differential) функції в точціxназивається диференціал від її диференціала першого порядку (за умови, що повторний приріст незалежної змінної x збігається з попереднім ) і позначається:

 

.

 

За означенням маємо

 

,

 

позначають . Таким чином

 

.                                     (3.16)

 

Аналогічно, диференціалом n-го порядку (позначається ),n=2,3,... називається диференціал від диференціала порядку за умови, що в диференціалах весь час беруться одні й ті самі приростинезалежної змінноїx. Тобто

 

.

 

При цьому справедлива формула:

 

.                                     (3.17)

 

 

Приклад 3.20. Обчислити , якщо.

Розв’язання. Скористаємось формулою (3.16). Для цього знайдемо :

, .

 

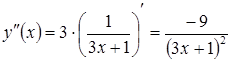Отже

.

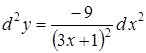3.5. Основні теореми диференціального числення

 

Теорема Ферма

Теорема 3.6. Нехай функція визначена на інтерваліі в деякій точцімає найбільше або найменше значення. Тоді якщо в точцііснує похідна, то вона дорівнює нулю, тобто.

Доведення. Нехай для визначеності функція в точцімає найбільше значення. Оскільки ми прийняли, що- найбільше значення, тодля довільної точки, звідки випливає, що (, якщо) і (, якщо).

Оскільки за умовою теореми похідна в точці існує, то, перейшовши до границі за умови, що, дістанемо:

 

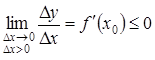 і .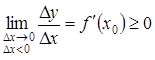

 

Але умови івиконуються одночасно, лише коли

.

 

Геометричний зміст теореми Ферма полягає в тому, що якщо в точці диференційовна функціямає найбільше або найменше значення, то в точцідотична до графіка функціїпаралельна осіOx.

 

Теорема Ролля

Теорема 3.7. Якщо функція 

1) неперервна на відрізку ,

2) має рівні значення на кінцях цього відрізка,

3) диференційовна в усіх точках інтервалу ,

то в цьому інтервалі існує принаймні одна точка ,, в якій похідна функції дорівнює нулю

 

.

Доведення. Оскільки неперервна на відрізку, то вона досягає на цьому відрізку свого найбільшогоM і найменшого m значень (друга теорема Вейєрштраcса). Отже .

Розглянемо два можливі випадки: 1) ; 2).

1) Нехай . Це можливо тільки за умови, щодля всіх, тоді для будь-якогоматимемо:.

2) Якщо . Тоді хоча б одне з цих значеньМ або m досягається всередині відрізка в деякій точці,. Нехай для конкретності.

Оскільки ми прийняли, що - найбільше значення і функція в точціс диференційовна, то за теоремою Ферма .

 

Зауваження. Між двома коренями функції завжди міститься корінь її похідної, якщо тільки функція задовольняє умови теореми Ролля (рис. 3.5).

 

Геометричний зміст теореми Ролля

 

Рис. 3.5

Рис. 3.6

 

Геометричний зміст теореми Ролля полягає в тому, що на графіку функції, яка задовольняє умови теореми, знайдеться принаймні одна точка , в якій дотична горизонтальна () (рис. 3.6).

 

Приклад 3.21. Перевірити справедливість теореми Ролля для функції на відрізку.

Розв’язування. Перевіримо виконання умов теореми:

1) – неперервна на відрізку;

2) ;

3) .

Отже, як ми бачимо, умови теореми виконуються. Неважко помітити, що існує точка в якій похідна дорівнює нулю.

 

Приклад 3.22. Довести, що друга похідна функції

 

 

принаймні в одній точці проміжку дорівнює нулю.

Розв’язання. Очевидно, що функція диференційовна на всій числовій осі і перетворюється в нуль в точках ,,. Тобто на кожному з відрізківівиконуються умови теореми Ролля. А отжеітакі, що,. Але для функціїумови теореми Ролля на відрізкутакож задовольняються: 1)всюди неперервна; 2); 3)диференційовна на всій числовій прямій (). Тому за теоремою Ролля, що, що і потрібно було довести.

 

Теорема Лагранжа (теорема про скінченні прирости)

Теорема 3.8. Якщо функція 

1) неперервна на відрізку ,

2) диференційовна в інтервалі ,

то в цьому інтервалі існує принаймні одна така точка ,, що має місце рівність:

 

.                                   (3.18)

 

Доведення. Побудуємо допоміжну функцію , де. Підберемотак, щоб функціяна кінцях відрізка мала рівні значення:

 

, .

 

.

 

Тоді

.

 

Функція задовольняє умови теореми Ролля. Вона: 1) неперервна на, 2), 3) диференційовна на. Отже, за цією теоремою знайдетьсятаке, що.

Знайдемо похідну . Тоді з умовиматимемо, що, звідки, що і потрібно було довести.

 

 

Геометричний зміст теореми Лагранжа

 

Рис. 3.7

На рис. 3.7 зображено графік функції , яка задовольняє умови теореми Лагранжа на відрізку. Відмітимо, що є кутовим коефіцієнтом хорди, що стягує дугу АВ, яка відповідає приросту ba. З іншого боку,   кутовий коефіцієнт дотичної в точці з абсцисою ,.

Отже, на гладкій дузі АВ графіка функції завжди знайдеться принаймні одна внутрішня точка, в якій дотична паралельна хорді, що стягує кінці дуги А і В.

Зауваження. Теорему Лагранжа можна записати через прирости:

 

.                         (3.19)

 

Приклад 3.23. На дузі АВ кривої знайти точкуМ, в якій дотична буде паралельна хорді, якщо ,.

Розв’язання. Функція неперервна і диференційовна для всіх значеньх. За теоремою Лагранжа між двома значеннями ііснує таке значення, що має місце рівність, отримана з (3.18)

,

де . Підставивши відповідні значення, дістанемо:

, ;.

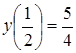Отже, маємо точку .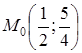

 

Теорема Коші (Cauchy theorem) (про відношення приростів двох функцій)

Теорема 3.9. Якщо функції і

1) неперервні на відрізку ,

2) диференційовні в інтервалі , причому,

то в цьому інтервалі існує точка ,така, що має місце рівність:

 

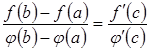.                               (3.20)

 

Доведення. Рівність (3.20) можлива, оскільки ,.

Побудуємо допоміжну функцію , де. Підберемотак, щоб функціяна кінцях відрізка мала рівні значення:

 

, .

 

.

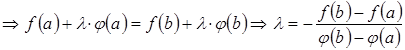Тоді

.

 

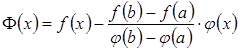Функція задовольняє умови теореми Ролля. Отже за цією теоремою знайдеться таке, що.

Знайдемо похідну 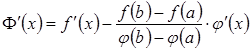. Тоді з умовиматимемо, що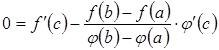, звідки

 

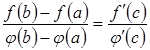, що і потрібно було довести.

 

Зауваження. Якщо в рівності (3.20) прийняти , то як наслідок отримаємо теорему Лагранжа (3.18).

 

3.6. Правила Лопіталя розкриття невизначеностей (L'Hospital rule)

 

Теорема 3.10. (І правило Лопіталя). Якщо:

1) функції ідиференційовні на інтервалі,для всіх;

2) ;

3) існує скінченна або нескінченна границя ,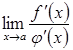

то існує границя 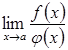, причому має місце рівність:

 

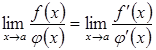.                              (3.21)

 

Доведення. Довизначимо функції ів точцітак, щоб вони стали неперервними, тобто покладемо. Теперці функції на відрізку, () задовольняють умови теореми Коші. Тому існує точкас, , () така, що

.

 

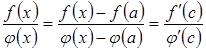Оскільки , () то. Перейшовши в останній рівності до границі, за умови, отримаємо

 

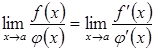 що і потрібно було довести.

 

Запам’ятай добре! Доведену теорему зазвичай називають правилом Лопіталя розкриття невизначеності за умови.

Аналогічні теореми мають місце для розкриття невизначеності у випадку односторонніх границь при,.

 

Приклад 3.24. Обчислити границю .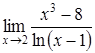

Розв’язання. Ми маємо невизначеність типу . Функціїізадовольняють умови теореми в деякому околі точки. Застосуємо правило Лопіталя:

 

.

 

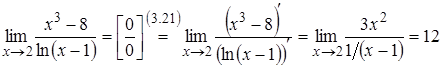Наслідок 1. Теорема Лопіталя справедлива також при , приі при.

 

Приклад 3.25. Обчислити границю .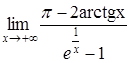

Розв’язання. Маємо невизначеність типу . Застосуємо правило Лопіталя:

.

 

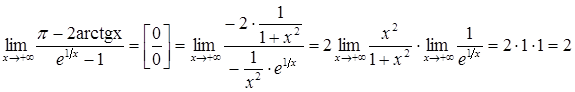Наслідок 2. Якщо похідні ізадовольняють ті самі вимоги, що і функціїі, то правило Лопіталя можна застосувати повторно. При цьому отримаємо

 

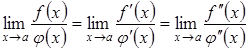.                       (3.22)

 

І взагалі, правило Лопіталя при виконанні умов теореми можна застосовувати багаторазово.

 

Приклад 3.26. Обчислити границю .

Розв’язання. Дана границя дозволяє використовувати формулу (3.21) багаторазово, дійсно:

 

.

 

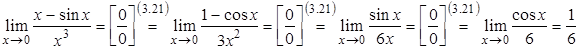Наслідок 3. Якщо в теоремі замінити умову 2) на наведену нижче

2) , або, то формула (3.21) також має місце.

В цьому випадку правило Лопіталя застосовується для розкриття невизначеності типу ( ІІ правило Лопіталя).

 

Приклад 3.27. Якщо , то

 

,

 

тобто довільний додатний степінь x зростає швидше, ніж при.

Розв’язування. Дійсно, застосувавши ІІ правило Лопіталя, отримаємо

 

.

 

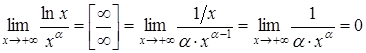Приклад 3.28. Якщо ,то

 

,

 

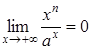тобто, при степенева функціязростає повільніше, ніж показникова функція,.

Розв’язування. Дійсно, застосувавши правило Лопіталя розкриття невизначеності  n раз, отримаємо:

 

.

 

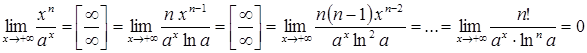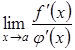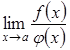Зазначимо, що формули (3.21), (3.22) мають місце лише тоді, коли існує скінченна або нескінченна границя . Але буває і так, що границяіснує, у випадку коли границя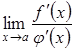не існує.

 

Приклад 3.29. існує і дорівнює.

Розв’язання. Дійсно

 

.

 

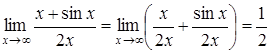Але відношення похідних 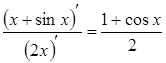не має границі при.

 

Після певних перетворень правило Лопіталя може бути застосовано також до розкриття інших невизначеностей, таких як: ,,,,.

Так, границі невизначеностей типів тадоцільно звести до видуабо.

 

Приклад 3.30. Обчислити границю .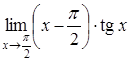

Розв’язання. Маємо невизначеність типу . Приведемо цю невизначеність до видуі застосуємо правило Лопіталя.

 

.

 

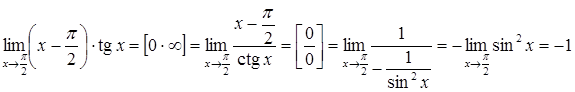Приклад 3.31. Обчислити границю .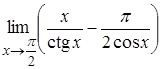

 

Розв’язання. Маємо невизначеність типу . Спочатку зведемо дроби до спільного знаменника.

 

.

 

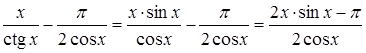Внаслідок перетворень ми дістали невизначеність виду . Застосуємо правило Лопіталя

 

.

 

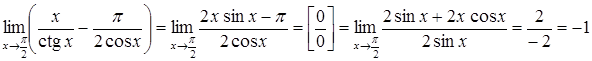При розкритті невизначеностей типу ,,за допомогою правила Лопіталя попередньо необхідно виконати деякі перетворення.

Нехай треба обчислити границю складеної степеневопоказникової функції:

,

 

де ми маємо невизначеність одного з вищезгаданих типів. Запишемо цю границю у вигляді

,

 

тут в показнику маємо вже невизначеність виду , яку можна звести до невизначеності типуабошляхом знесення в знаменник одного із співмножників, що стоять під знаком границі.

Приклад 3.32. Обчислити границю .

Розв’язання. Маємо невизначеність типу . Виконаємо тотожне перетворення функції:

.

 

Знайдемо границю показника отриманої функції за правилом Лопіталя

 

.

 

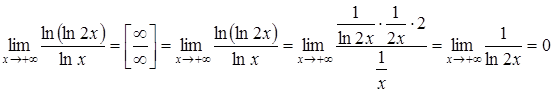Отже, .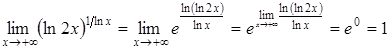

 

Приклад 3.33. Обчислити границю .

Розв’язання. Маємо невизначеність типу . Виконаємо тотожне перетворення функції, що стоїть під знаком границі:

.

 

Обчислимо окремо границю, яка міститься в показнику, за правилом Лопіталя

.

Отже,

.