2.6. Техніка обчислення границь

 

1. Безпосереднє обчислення границь шляхом підстановки граничного значення та використання основних теорем про границю.

 

Приклад 2.5. .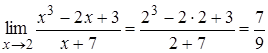

 

Приклад 2.6. .

 

Приклад 2.7. .

Запам’ятай добре!

1) Якщо при підстановці граничного значення одержуємо різницю або частку нескінченно великих, то кажуть, що ми маємо невизначеність (ambiguity, uncertainty) типу або.

2) Відношення нескінченно малих величин називають невизначеністю типу , а добуток нескінченно малої на нескінченно велику називається невизначеністю типу.

 

 

2. Розкриття невизначеностей типу , якщо під знаком границі стоїть дробово-раціональна функція(fractional rational function) , де

,

, ().

 

а) Якщо , то;

б) якщо , то;

в) якщо , то,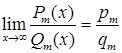

оскільки ,і

 

.

 

 

 

Приклад 2.8. .

 

Приклад 2.9. .

Приклад 2.10. .

 

Приклад 2.11. .

 

Приклад 2.12. .

 

 

 

3. Розкриття невизначеностей типу , коли під знаком границі стоїть вираз виду ().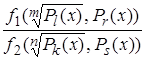

Як правило, при розкритті таких невизначеностей кожен многочлен під знаком границі заміняють на еквівалентний () та, виконавши необхідні скорочення, обчислюють цю границю.

 

 

Приклад 2.13.

.

 

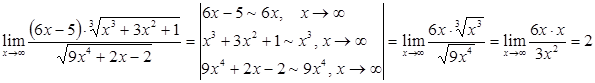Приклад 2.14. .

Розв’язання. Тут ми маємо невизначеність типу . Перейдемо до невизначеності. Для цього зведемо до спільного знаменника вирази, дістанемо

 

.

 

4. Розкриття невизначеностей типу  з ірраціональними виразами під знаком границі ().

Для розкриття таких невизначеностей потрібно домножити та поділити вираз, що стоїть під знаком границі, на спряжений. Виконавши необхідні перетворення обчислюємо дану границю.

 

Приклад 2.15. .

Розв’язання. Домножимо вираз, що стоїть під знаком на границі, на спряжений:

.

 

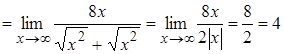Приклад 2.16. .

Розв’язання. Домножимо вираз, що стоїть під знаком на границі, на спряжений:

 

 

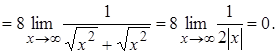
5. Розкриття невизначеностей типу  при , коли під знаком границі стоїть відношення многочленів.

 

Для розкриття таких невизначеностей потрібно виділити в чисельнику та знаменнику дробу, що знаходиться під знаком границі, множник . Виконавши необхідні скорочення обчислюємо дану границю.

 

Приклад 2.17. .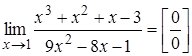

Розв’язання. Маємо невизначеність виду . Оскільки примногочлени, що стоять в чисельнику і знаменнику, перетворюються на нуль, то за теоремою Безу вони розкладаються на множники, серед яких обов’язково присутній множник.

В чисельнику виконаємо ділення нав стовпчик:

 

, тоді .

 

Оскільки добуток коренів знаменника , один з них, то другий. Отже,розкладається на множники:

 

.

 

Маємо .

 

Приклад 2.18 .

Розв’язання. Маємо невизначеність виду . Оскільки примногочлени, що стоять в чисельнику і знаменнику, перетворюються в нуль, то за теоремою Безу вони розкладаються на множники, серед яких обов’язково присутній множник.

В чисельнику виконаємо ділення нав стовпчик:

 

, тоді .

 

Оскільки добуток коренів знаменника , один з них, то другий. Отже,розкладається на множники:.

 

Маємо .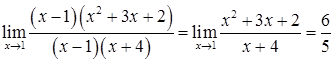

 

6. Розкриття невизначеностей типу  при з використанням таблиці еквівалентних величин.

 

Приклад 2.19

.

 

 

Приклад 2.20

.

 

Приклад 2.21. Довести, що при н. м.ібудуть еквівалентними.

Розв’язання. Знайдемо границю відношення цих функцій.

 

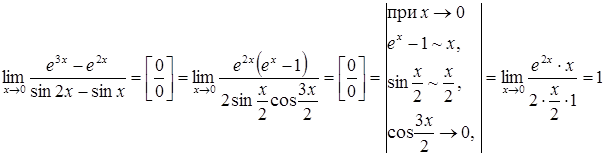Отже, за означенням ці величини еквівалентні.

 

Запам’ятай добре! В тих випадках, коли потрібно розкрити невизначеність типу , її зводять шляхом елементарних перетворень до невизначеностей типуабо, які розкривають, використовуючи таблицю еквівалентностей.

 

Приклад 2.22. .

Розв’язання. Перейдемо до іншої невизначеності. Для цього використаємо властивості логарифмічної функції:

 

.

 

Приклад 2.23. .

Розв’язання. Перетворимо невизначеність в невизначеність(це завжди можна зробити), після чого приведемо границю до виду, коли можливе застосування еквівалентних перетворень.

.

 

Приклад 2.24. .

Розв’язання. Маємо невизначеність виду . Оскільки примногочлен в чисельнику перетворюється в нуль (- корінь чисельника), то за теоремою Безу він розкладається на множники, один з яких. За теоремою Вієта другий корінь. Тому. Маємо

.

 

Приклад 2.25. .

Розв’язування. Перейдемо до іншої невизначеності. Для цього використаємо властивості логарифмічної функції:

 

.

Оскільк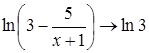и при, то невизначеності в останній границі немає і

 

.

 

7. Розкриття невизначеностей типу  при з ірраціональними виразами під знаком границі.

 

Для розкриття таких невизначеностей потрібно домножити і поділити вираз, що стоїть під знаком границі, на спряжений до виразу, який містить ірраціональність. Виконавши необхідні перетворення обчислюємо дану границю.

 

Приклад 2.26. .

Розв’язання. Маємо невизначеність виду . Для її розкриття потрібно звільнитися від ірраціональності у чисельнику. З цією метою помножимо чисельник і знаменник дробу на вираз.

 

.

 

Оскільки при многочленв знаменнику перетворюється в нуль, то за теоремою Безу знаменник ділиться на різницюбез остачі. Виконаємо діленнянав стовпчик:

 

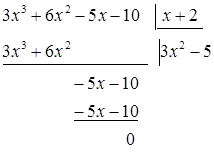, тоді .

 

Отже,

.

 

Приклад 2.27. 

Розв’язання. Маємо невизначеність виду . Для її розкриття потрібно звільнитися від ірраціональності у чисельнику та знаменнику. З цією метою помножимо чисельник і знаменник дробу на вираз. Маємо:

 

 

 

 

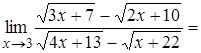
8. Розкриття невизначеності типу з використанням другої важливої границі

 

,                                      (*)

тут довільна н. м. функція.

 

Приклад 2.28. .

Розв’язання. Спосіб І. Маємо невизначеність . Виконаємо тотожні перетворення, які приведуть границю до виду (*)

.

Вираз, що знаходиться в квадратних дужках, приведено до виду (*), де при, тому. Отже, матимемо:

 

.

Спосіб ІІ.

 

.

 

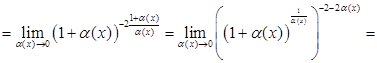
Приклад 2.29. .

Розв’язання. Спосіб І. Маємо невизначеність . Виконаємо тотожні перетворення, які приведуть границю до виду (*)

 

.

 

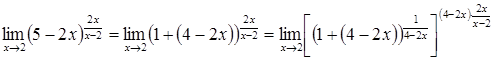Вираз, що знаходиться в квадратних дужках, приведено до виду (*), де при, тому. Отже, матимемо:

 

.

 

Спосіб ІІ.

 

.
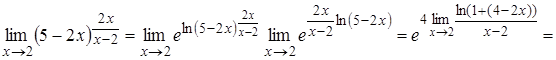