Тема 1. Вступ до математичного аналізу

 

1.2. Побудова графіків функцій шляхом елементарних перетворень

 

При побудові графіка функції використовують в певній послідовності перетворення графіка функції. Ці перетворення можна виконати, наприклад, в такій послідовності.

а) Будуємо графік .

б) Графік функції ,k>0 дістанемо стискуванням графіка а) в k разів вздовж осі абсцис до осі ординат для випадку k>1, або розтягуванням в 1/k раз вздовж осі абсцис від осі ординат у випадку 0<k<1. Стискування графіка вздовж осі абсцис в k раз (k>1) здійснюється так: абсциса кожної точки зменшується в k раз, ордината при цьому залишається незмінною (кожна точка М(x, y) графіка переходить у точку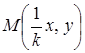графіка).

Якщо ж k<0, то можна спочатку побудувати графік , а потім відобразити його симетрично відносно осі ординат.

в) Графік ,m>0 дістанемо розтягуванням графіка б) в m разів вздовж осі ординат відносно осі абсцис для випадку m>1, або стискуванням в 1/m раз вздовж осі ординат відносно осі абсцис у випадку 0<m<1. Розтягування графіка вздовж осі ординат в m раз (m>1) здійснюється так: ордината кожної точки збільшується в m раз, абсциса при цьому залишається незмінною (кожна точка М(x,y) графіка переходить у точкуграфіка).

У випадку m<0 можна спочатку побудувати графік , а потім відобразити його симетрично відносно осі абсцис.

г) Графік функції або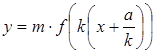,k>0 дістанемо паралельним перенесенням графіка в) вліво вздовж осі Ox на одиниць дляa>0 і вправо на дляa<0.

д) Графік функції дістанемо паралельним перенесенням графіка г) вгору наbодиниць вздовж осі Oy для b>0 і вниз на для b<0.

Розглянуті перетворення можна виконувати у будь-якому порядку, але величини, на які графік переноситься вздовж координатних осей, залежать від порядку перетворень.

Проілюструємо побудову графіка функції за наведеним алгоритмом.

 

Приклад 1.3. Побудувати графік функції .

Розв’язання

а) За вихідний беремо графік функції . Для зручності розглянемо побудову графіка тільки на одному періоді.

 

 

б) Оскільки , то стискаємо графік функціїв два рази вздовж осіOx. Дістаємо графік функції .

 

 

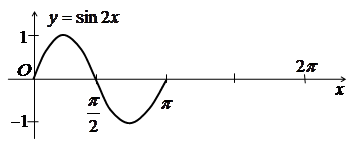
в) Розтягуємо графік функції в три рази вздовж осіOy, оскільки . Дістаємо графік функції.

 

 

г) Симетрично відобразивши останній графік відносно осі Ox, дістанемо графік функції .

 

д) Отриманий графік паралельно переносимо на вправо вздовж осіOx, дістанемо графік функції або.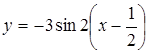

 

 

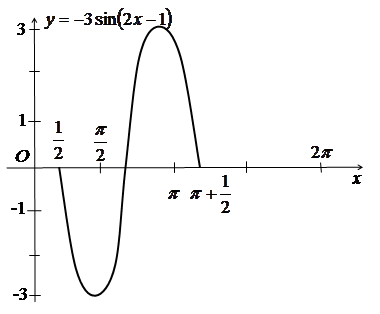
е) Нарешті, отриманий графік паралельно перенесемо на дві одиниці вгору вздовж осіOy, оскільки b=2>0. Дістанемо графік функції (рис. 1.3).

Рис. 1.3

 

 

Приклад 1.4. Побудувати графік функції .

Розв’язання

Область існування функції: .

Поділивши чисельник на знаменник, дістанемо

 

, або .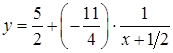

 

 

Графік такої функції можна отримати з графіка функції за допомогою таких перетворень:

а) паралельного перенесення графіка вздовж осі абсцис наодиниць вліво;

б) розтягування графіка а) вздовж осі ординат в раз;

в) симетричного відображення графіка б) відносно осі абсцис;

в) паралельного перенесення вздовж осі ординат на одиниць вгору.

Будуємо схематичний графік функції (рис. 1.4).

 

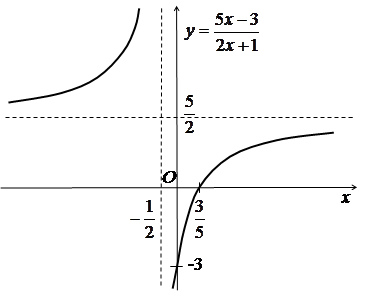
Рис. 1.4