
Задачі з фізики для ІнМТ (Ат)
.docxМІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ВІННИЦЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ
Кафедра загальної фізики та фотоніки
КОНТРОЛЬНА РОБОТА З ФІЗИКИ
Виконав:
Перевірив:
Вінниця-2014
Задача 1.
Обчислити
індукцію магнітного поля на осі соленоїда,
якщо кількість витків на одиницю його
довжини
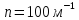 ,
а сила струму у витках
,
а сила струму у витках
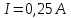 .
.
Дано:
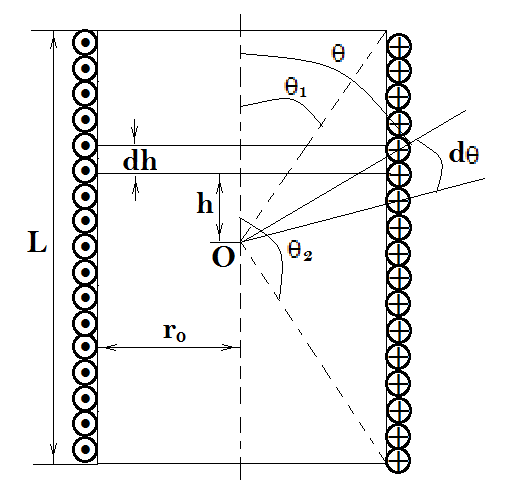
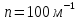
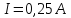


Розв'язування.
Соленоїдом
називають сукупність спірально намотаних
на циліндричну поверхню витків
ізольованого провідника, по якому
проходить електричний струм. Як правило,
вважають, що провідник намотаний в один
шар щільно, рівномірно і кількість
витків обмотки на одиницю довжини
циліндричної поверхні є величина сталою
і дорівнює
 .
Нехтуючи зазором між витками при щільній
упаковці їх, можна вважати, що
.
Нехтуючи зазором між витками при щільній
упаковці їх, можна вважати, що
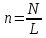 ,
де
,
де
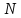 – загальна кількість витків соленоїда,
а
– загальна кількість витків соленоїда,
а
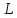 – його довжина. У такому разі соленоїд
можна вважати сукупністю кілець зі
струмом і тоді для обчислення індукції
магнітного поля в довільній точці його
осі можна скористатися формулою
– його довжина. У такому разі соленоїд
можна вважати сукупністю кілець зі
струмом і тоді для обчислення індукції
магнітного поля в довільній точці його
осі можна скористатися формулою
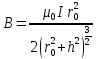 – індукція магнітного поля на осі
колового струму.
– індукція магнітного поля на осі
колового струму.
Якщо
довжина соленоїда
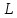 більше ніж у 10 разів перевищує діаметр
його витків
більше ніж у 10 разів перевищує діаметр
його витків
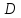 ,
то такий соленоїд називають нормальним
(нехтують крайовими ефектами). Особливістю
такого соленоїда є те, що всередині його
вздовж осі магнітне поле має однаковий
напрям і однакове в усіх точках значення,
тобто є однорідним.
,
то такий соленоїд називають нормальним
(нехтують крайовими ефектами). Особливістю
такого соленоїда є те, що всередині його
вздовж осі магнітне поле має однаковий
напрям і однакове в усіх точках значення,
тобто є однорідним.
Розрахуємо
індукцію магнітного поля, наприклад у
точці О осі нормального соленоїда (див.
рисунок). Для цього виділимо спочатку
вузьку (плоску) смугу витків соленоїда
завтовшки
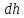 ,
розміщену між проведеними з точки О
радіусами
,
розміщену між проведеними з точки О
радіусами
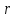 ,
які утворюють з віссю соленоїда кути
,
які утворюють з віссю соленоїда кути
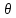 і
і
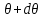 .
Довжина цієї смуги
.
Довжина цієї смуги
 .
Кількість витків
.
Кількість витків
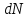 ,
що укладаються на виділеній смузі,
,
що укладаються на виділеній смузі,
 .
.
Елементарна
індукція магнітного поля
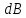 ,
створювана в точці О витками
,
створювана в точці О витками
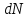 провідника зі струмом І,
за формулою
провідника зі струмом І,
за формулою
 буде такою:
буде такою:
 .
.
Оскільки
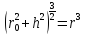 ,
а
,
а
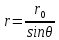 ,
то
,
то
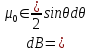 .
.
Щоб
знайти результуюче значення індукції
магнітного поля в точці О, проінтегруємо
останню формулу у межах кутів
 і
і
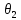 :
:
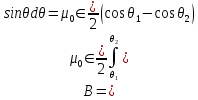 .
.
Для
нескінченно довгого соленоїда
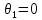 і
і
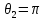 .
Тоді
.
Тоді
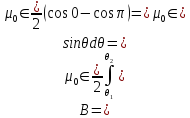 .
.
Для
довільної основи соленоїда (наприклад,
у центрі верхньої основи
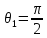 і
і
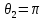 )
)
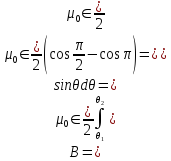 ,
,
Тобто у два рази менша, ніж на осі всередині соленоїда.
Для нашої умови задачі після підстановки числових значень отримаємо:
а) в центрі соленоїда:
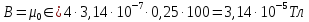 ;
;
б) в центрі верхньої основи:
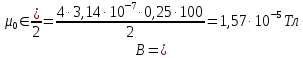 .
.
Відповідь:
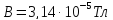 ,
,
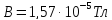 .
.
Задача 2 .
Матеріальна
точка здійснює прямолінійний рух (вздовж
осі Ох), кінематичне рівняння руху якої
має такий вигляд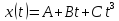 ,
де
,
де
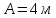 ,
,
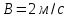 ,
,
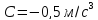 .
Визначити координату точки,
миттєву швидкість
.
Визначити координату точки,
миттєву швидкість
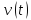 та
прискорення
та
прискорення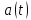 для моменту часу
для моменту часу
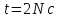 після
початку руху, де
після
початку руху, де
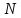 -
номер варіанту.
-
номер варіанту.
Дано:
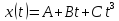
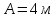
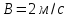
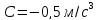
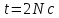

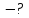
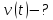
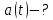
Розв’язування.
Координату
точки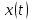 знаходимо,в рівняння руху підставляємо
час
знаходимо,в рівняння руху підставляємо
час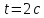 :
:
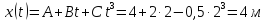 .
.
Миттєву
швидкість
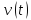 знаходимо, продиферинціювавши координату
знаходимо, продиферинціювавши координату
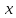 за
часом
за
часом
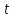 (взяти
похідну):
(взяти
похідну):
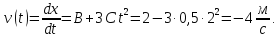 Знак мінус вказує на те, що в заданий
момент часу точка рухається в від’ємному
напрямку координатної осі Ох.
Знак мінус вказує на те, що в заданий
момент часу точка рухається в від’ємному
напрямку координатної осі Ох.
Миттєве
прискорення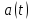 в довільний момент часу, знаходимо,
взявши другу похідну від координати
в довільний момент часу, знаходимо,
взявши другу похідну від координати
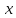 за
часом
за
часом
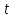 або першу похідну від швидкості за
часом
або першу похідну від швидкості за
часом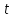 :
:
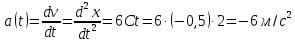 .
Знак мінус вказує на те, що в заданий
момент часу прискорення направлено в
від’ємному напрямку координатної осі
Ох.
.
Знак мінус вказує на те, що в заданий
момент часу прискорення направлено в
від’ємному напрямку координатної осі
Ох.
Відповідь: 4м, -4м/с, -6 м/с2.
Задача 3.
Матеріальна
точка здійснює обертальний рух,
кінематичне рівняння руху якої має
такий вигляд
 ,
де
,
де
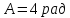 ,
,
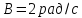 ,
,
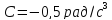 .
Визначити кутову координату точки,
миттєву кутову швидкість
.
Визначити кутову координату точки,
миттєву кутову швидкість
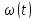 та кутове прискорення
та кутове прискорення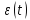 для моменту часу
для моменту часу
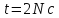 після початку руху, де
після початку руху, де
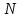 -
номер варіанту.
-
номер варіанту.
Дано:
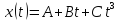

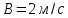
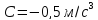
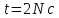

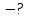
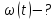

Розв’язування.
Кутову
координату точки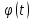 знаходимо, в рівняння руху підставляємо
час
знаходимо, в рівняння руху підставляємо
час
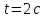 :
:
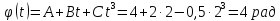 .
.
Миттєву
кутову швидкість
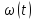 знаходимо, продиферинціювавши кутову
координату
знаходимо, продиферинціювавши кутову
координату
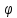 за
часом
за
часом
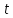 (взяти
похідну):
(взяти
похідну):
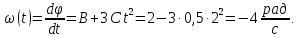
Миттєве
кутове прискорення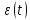 в довільний момент часу, знаходимо,
взявши другу похідну від кутової
координати
в довільний момент часу, знаходимо,
взявши другу похідну від кутової
координати
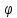 за
часом
за
часом
 або першу похідну від кутової швидкості
за часом
або першу похідну від кутової швидкості
за часом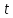 :
:
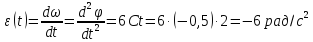 .
.
Відповідь: 4рад, -4рад/с, -6 рад/с2.
Задача 4.
Тіло
обертається навколо нерухомої осі.
Залежність кута повороту тіла від часу
задана рівнянням
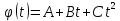 ,
де
,
де

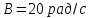 ,
,
 .
Знайти модуль повного прискорення точки
.
Знайти модуль повного прискорення точки
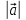 ,
розміщеної на відстані
,
розміщеної на відстані
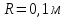 від осі обертання, в момент часу
від осі обертання, в момент часу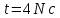 ,
де
,
де
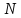 -
номер варіанту.
-
номер варіанту.
Дано:
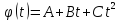

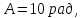
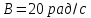

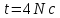
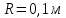

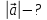
Розв’язування.
Повне
прискорення точки
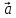 ,
яка рухається по кривій лінії, можна
знайти як геометричну суму тангенціального
прискорення
,
яка рухається по кривій лінії, можна
знайти як геометричну суму тангенціального
прискорення
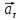 ,
направленого по дотичній до траєкторії,
та нормального прискорення
,
направленого по дотичній до траєкторії,
та нормального прискорення
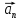 ,
направленого до центра кривизни
траєкторії:
,
направленого до центра кривизни
траєкторії:
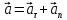 (1)
(1)
Оскільки
вектори взаємно перпендикулярні, то
модуль повного прискорення :
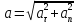 .
(2)
.
(2)
Тангенціальне та нормальне прискорення точки тіла, що обертається, виражаються за формулами:
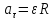 ,
,
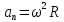 ,
,
де
 -кутове
прискорення тіла;
-кутове
прискорення тіла;
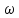 – кутова швидкість тіла.
– кутова швидкість тіла.
Замінимо
у формулі (2)
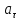 і
і
 на відповідні вирази. Тоді знайдемо:
на відповідні вирази. Тоді знайдемо:
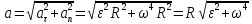 .
(3)
.
(3)
Кутову
швидкість
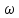 обчислюємо за першою похідною від кута
повороту за часом
обчислюємо за першою похідною від кута
повороту за часом
 :
:
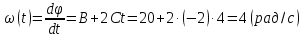 .
.
Кутове
прискорення
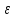 знаходимо, взявши першу похідну від
кутової швидкості
знаходимо, взявши першу похідну від
кутової швидкості
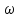 за часом
за часом
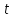 :
:
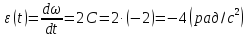 .
.
Кутове
прискорення заданого руху є сталим,
тобто не залежить від часу. Підставимо
значення
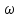 і
і
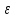 та задане значення
та задане значення
 у формулу (3):
у формулу (3):
 =0,1
=0,1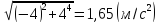 .
.
Відповідь: 1,65 м/с2.
Задача 5.
Матеріальна
точка масою
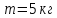 рухається по колу радіусом
рухається по колу радіусом
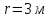 в площині ХОУ, причому рух її заданий
такими кінематичними рівняннями:
в площині ХОУ, причому рух її заданий
такими кінематичними рівняннями:
 ;
;
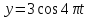 .
Визначити силу
.
Визначити силу
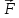 ,
яка діє на цю точку в момент часу
,
яка діє на цю точку в момент часу
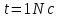 ,
де
N
–
номер варіанту.
,
де
N
–
номер варіанту.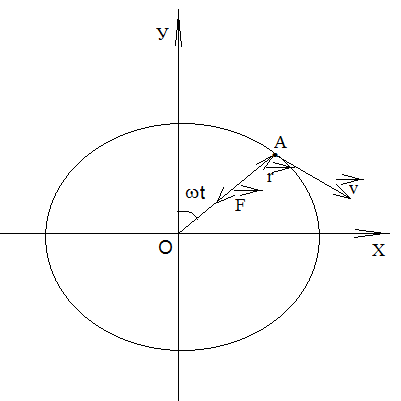
Дано:

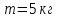
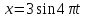
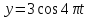
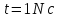

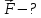
Розв’язування.
За
відомими кінематичними рівняннями руху
точки
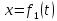 ,
,
 ,
,
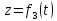 та
її масою знайти силу, що діє на точку в
будь-який момент часу.
та
її масою знайти силу, що діє на точку в
будь-який момент часу.
Розв’язок цієї задачі одержуємо безпосередньо з другого закону Ньютона в диференціальній формі. Для цього знаходимо проекції сили на осі координат:
 ,
,
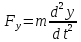 ,
,
 ,
за проекціями сили визначаємо модуль
сили
,
за проекціями сили визначаємо модуль
сили
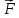 :
:
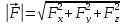 ,
а
також її напрямок у будь-який момент
часу
,
а
також її напрямок у будь-який момент
часу
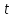 .
.
Із заданих рівнянь знаходимо проекції прискорення на осі координат:
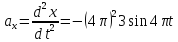 ,
,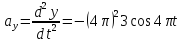 .
.
Помноживши ці рівняння на масу матеріальної точки, дістанемо проекції сили на ці осі:
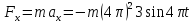 ,
,
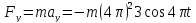 .
.
Модуль шуканої сили визначимо за формулою:
 .
.
Після підстановки числових значень отримаємо:
 .
.
Визначимо
напрямок сили
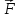 .
Для цього знайдемо напрямні косинуси:
.
Для цього знайдемо напрямні косинуси:
 ;
;
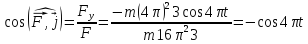 .
.
Одночасно
напрямні косинуси радіуса-вектора
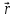 можна виразити так:
можна виразити так:
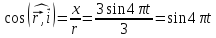 ;
;
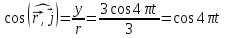 .
.
Отже,
ці вектори спрямовані по одній прямій,
але в різні боки. Тому силу визначають
за такою формулою:
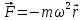 .
З цього
рівняння видно, що сила притягувальна,
оскільки її напрямок протилежний до
напрямку радіуса-вектора і вона
пропорційна масі точки та її відстані
до центра притягання, який знаходиться
в центрі кола.
.
З цього
рівняння видно, що сила притягувальна,
оскільки її напрямок протилежний до
напрямку радіуса-вектора і вона
пропорційна масі точки та її відстані
до центра притягання, який знаходиться
в центрі кола.
Відповідь: 2366,3 Н.
Задача 6.
Два
джерела струму з електрорушійними
силами
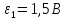 та
та
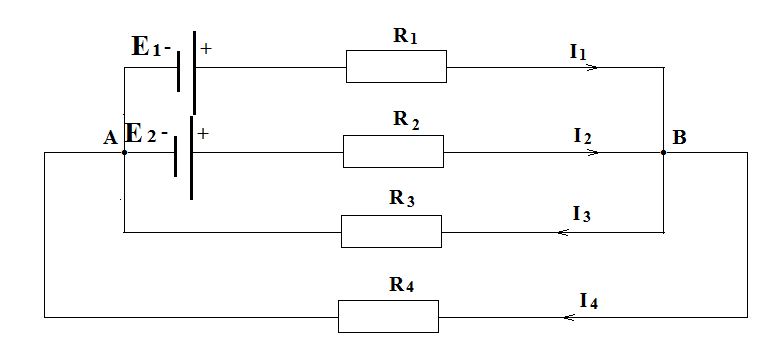
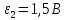 під’єднані в коло постійного струму,
електрична схема якого показана на
рис.1. Внутрішній опір кожного джерела
струму
під’єднані в коло постійного струму,
електрична схема якого показана на
рис.1. Внутрішній опір кожного джерела
струму
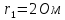 ,
,
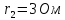 .
Опір зовнішнього навантаження
.
Опір зовнішнього навантаження
 .
Знайти
струми
.
Знайти
струми
 на кожній вітці електричного кола.
на кожній вітці електричного кола.
Дано:

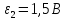


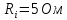
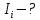
Розв'язування.
Відповідно до першого правила Кірхгофа алгебраїчна сума сили струмів в електричному вузлі дорівнює нулю. Для цього слід врахувати правило знаків: струмам які входять до електричного вузла надають знак «плюс», а струмам, які виходять з електричного вузла надають знак «мінус».
Математично це записується так:
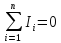 .
.
Для нашої електричної схеми, зокрема для вузла А маємо:
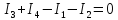 .
(1)
.
(1)
Відповідно
до другого правила Кірхгофа алгебраїчна
сума електрорушійних сил Е в замкнутому
електричному контурі дорівнює сумі
спадів напруг на кожному елементі
контура, враховуючи спад напруги на
джерелі. Для цього теж враховують правило
знаків: якщо струм за напрямком співпадає
з вибраним напрямком обходу контура
(за годинниковою стрілкою), то відповідний
спад напруги (добуток струму на опір
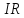 )
входить в рівняння з знаком «плюс», в
іншому випадку спад напруги входить в
рівняння з знаком «мінус».
Якщо
електрорушійна сила Е при обході контура
змінює свій знак всередині джерела з
«мінуса» на «плюс», то її приписують
знак «плюс», в іншому випадку її приписують
знак «мінус».
)
входить в рівняння з знаком «плюс», в
іншому випадку спад напруги входить в
рівняння з знаком «мінус».
Якщо
електрорушійна сила Е при обході контура
змінює свій знак всередині джерела з
«мінуса» на «плюс», то її приписують
знак «плюс», в іншому випадку її приписують
знак «мінус».
За
другим правилом Кірхгофа отримаємо
відповідно для контурів:
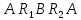 ,
,
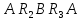 ,
,
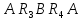 такі
рівняння:
такі
рівняння:
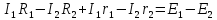 ,
(2)
,
(2)
 ,
(3)
,
(3)
 .
(4)
.
(4)
Підставимо в рівняння (2)-(4) значення відповідних опорів і електрорушійних сил, тоді отримаємо систему лінійних рівнянь:
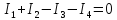 ,
,
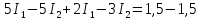 ,
,
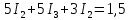 ,
,
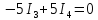 .
.
Необхідно розв’язати систему чотирьох лінійних рівнянь з чотирма невідомими. Для цього можна використати різні методи, зокрема метод Гаусса, метод детермінантів. Для цього перепишемо рівняння в наступному вигляді:
 ,
,
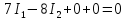 ,
,
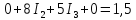 ,
,
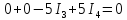 .
.
Значення відповідних струмів знайдемо із таких виразів:
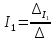 ,
,
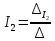 ,
,
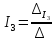 ,
, ,
,
де
 - визначник системи рівнянь;
- визначник системи рівнянь;
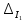 ,
,
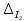 ,
,
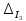 ,
,
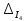 -
визначники,
отримані заміною відповідних стовпців
визначника
-
визначники,
отримані заміною відповідних стовпців
визначника
 стовпцями, складеними із вільних членів
чотирьох рівнянь системи. Знайдемо:
стовпцями, складеними із вільних членів
чотирьох рівнянь системи. Знайдемо:

 ,
,
 ,
,
 ,
,
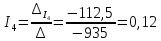 .
.
Задача 7.
Визначити
електричну ємність С плоского конденсатора
з двома шарами діелектриків: фарфору
товщиною
 і ебоніту товщиною
і ебоніту товщиною
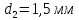 ,
якщо площа пластин рівна
,
якщо площа пластин рівна
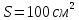 .
.
Дано:
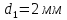
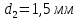
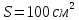
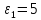
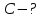
Розв’язування.
Ємність
конденсатора, за означенням,
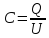 ,
де
,
де
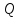 – заряд
на пластинах конденсатора;
– заряд
на пластинах конденсатора;
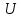 – різниця
потенціалів пластин. Замінимо в цій
рівності загальну різницю потенціалів
– різниця
потенціалів пластин. Замінимо в цій
рівності загальну різницю потенціалів
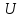 конденсатора сумою напруг на шарах
діелектриків
конденсатора сумою напруг на шарах
діелектриків
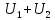 ,
отримаємо
,
отримаємо
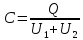 .
(1)
.
(1)
Прийнявши
до уваги,
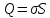 ,
,
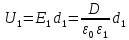 і
і
 ,
рівність (1) можна переписати у вигляді
,
рівність (1) можна переписати у вигляді
 ,
(2)
,
(2)
де
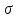 – поверхнева густина електричного
заряду на пластинах;
– поверхнева густина електричного
заряду на пластинах;
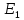 і
і
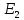 – напруженості поля в першому і в другому
шарі діелектрика відповідно;
– напруженості поля в першому і в другому
шарі діелектрика відповідно;
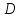 –
зміщення поля в діелектрику.
–
зміщення поля в діелектрику.
Помноживши,
чисельник і знаменник рівності (2) на
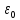 і враховуючи, що
і враховуючи, що
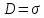 ,
остаточно отримаємо
,
остаточно отримаємо
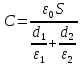 .
.
Зробивши обчислення в останній формулі, знайдемо
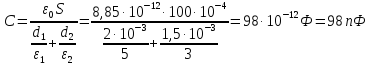 .
.
Відповідь: 98 пФ.
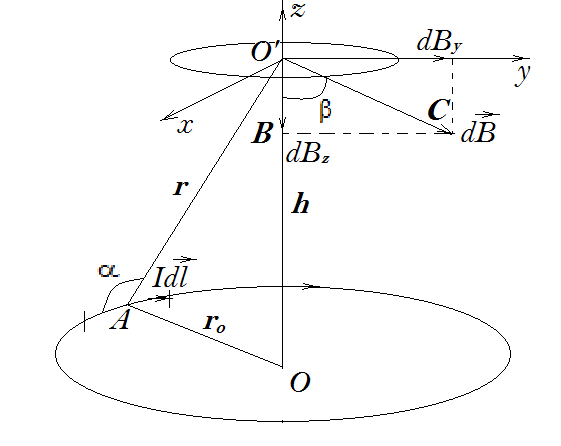
Задача 8.
Обчислити
індукцію магнітного поля
 лінійного колового провідника радіуса
лінійного колового провідника радіуса
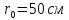 ,
по якому проходить струм силою
,
по якому проходить струм силою
 у точці
у точці
 ,
віддаленій уздовж осі Oz
від
центра кола О на відстань
,
віддаленій уздовж осі Oz
від
центра кола О на відстань
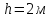 (рисунок).
(рисунок).
Дано:
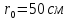 0,5
м
0,5
м

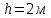
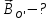
Розв'язування.
Щоб
обчислити індукцію магнітного поля
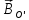 в точці O’
на відстані
в точці O’
на відстані
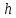 від лінійного колового провідника зі
струмом, поділимо його на нескінченно
малі елементи
від лінійного колового провідника зі
струмом, поділимо його на нескінченно
малі елементи
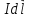 і обчислимо спочатку за законом
Біо-Савара-Лапласа індукцію
і обчислимо спочатку за законом
Біо-Савара-Лапласа індукцію
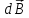 ,
створювану елементом
,
створювану елементом
 :
:
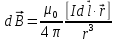 ,
або (1)
,
або (1)
 ,
(2)
,
(2)
де
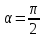 .
Вектор
.
Вектор
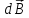 перпендикулярний до площини, в якій
лежать вектори
перпендикулярний до площини, в якій
лежать вектори
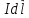 та
та
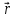 ,
і направлений до осі ОО’
під
кутом
,
і направлений до осі ОО’
під
кутом
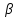 .
Тому проекція
.
Тому проекція
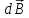 на вісь Oz
на вісь Oz
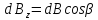 ,
а
на вісь Oy
-
,
а
на вісь Oy
-
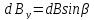 .
.
Визначивни
відповідні
проекції елементарних індукцій від
інших елементів струму
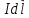 ,
на які можна розбити увесь коловий
струм, помітимо, що всі проекції на осі
Ox
I
Oy
елементарних
індукцій взаємно компенсуються і
результуючі значення цих проекцій
дорівнюватимуть нулеві
,
на які можна розбити увесь коловий
струм, помітимо, що всі проекції на осі
Ox
I
Oy
елементарних
індукцій взаємно компенсуються і
результуючі значення цих проекцій
дорівнюватимуть нулеві
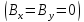 ,
а проекції на вісь Oz
будуть
направлені вздовж осі Oz
в один бік. Тому їх можна додавати
алгебраїчно, тобто
,
а проекції на вісь Oz
будуть
направлені вздовж осі Oz
в один бік. Тому їх можна додавати
алгебраїчно, тобто
