
- •1 Вопрос
- •2 Вопрос.
- •4.Уравнения с разделяющимися переменными.
- •6 Вопрос
- •7 Вопрос.
- •Теорема.
- •8. Комплексные числа
- •9. Линейные дифференциальные уравнения с постоянными коэффициентами
- •Решение неоднородных дифференциальных уравнений с постоянными коэффициентами (лнду).
- •12. Перестановки. Размещения. Сочетания.
- •13. Понятие случайного события. Невозможное и достоверное события. Несовместные события. Сумма и произведение случайных событий.
- •Классическое определение вероятности.
- •Условная вероятность. Независимые события. Теорема умножения вероятностей.
- •Теорема сложения вероятностей.
- •17. Формула полной вероятности и формула Байеса.
- •Дискретные случайные величины и их характеристики.
- •24 .Геометрическое распределение.
- •26.Равномерное распределение.
- •27.Показательное распределение.
- •29. Теоремы Лапласа
- •30. Система случайных величин. Основные понятия. Ковариация. Коэффициент корреляции
-
Теорема сложения вероятностей.
Пусть
события
![]() попарно несовместны. Тогда для суммы
попарно несовместны. Тогда для суммы
![]()
этих
событий можно утверждать, что мера
множества благоприятных исходов события
В есть сумма мер множеств событий
![]() .
Отсюда следует теорема сложения для
несовместных событий:
.
Отсюда следует теорема сложения для
несовместных событий:
![]()
Рассмотрим
теперь два совместых события
![]() и
и![]() Эти события, а также их сумму, можно
представить в виде суммы несовместных
событий:
Эти события, а также их сумму, можно
представить в виде суммы несовместных
событий:
![]()
![]()
![]()
Тогда
![]() (6.6)
(6.6)
![]() (6.7)
(6.7)
![]() (6.8)
(6.8)
Сложив первые (1.13) и (1.14), получим
![]()
Заметим, что последние три слагаемые здесь есть правая часть равенства (6.8), отсюда
![]()
получаем теорему сложения для двух совместных событий:
![]()
Теорема сложения для n совместных событий записывается так:
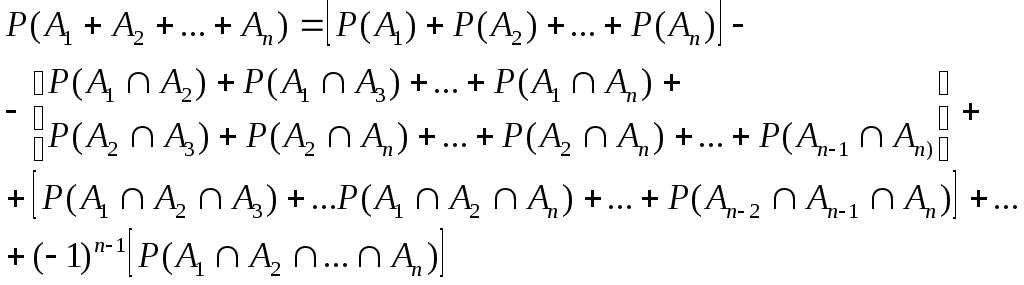 (6.9)
(6.9)
В частном случае, при n=3, теорема запишется так:
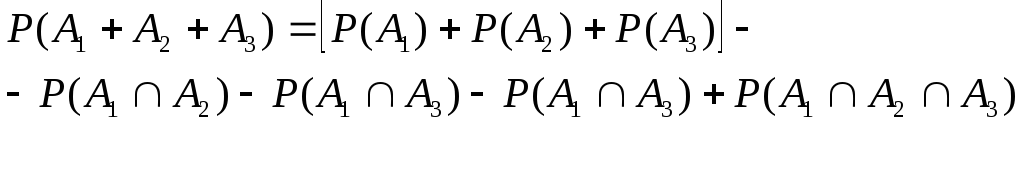 (6.10)
(6.10)
17. Формула полной вероятности и формула Байеса.
Рассмотрим некоторое событие А и группу событий
![]()
Пусть
эта группа событий является полной
группой событий по отношению к событию
А. В частном случае, (см п.2) она может
быть и полной группой событий вообще.
То есть, события попарно несовместны
(первое условие) и из наступления события
А следует наступление одного из событий
в группе. При выполнении этих двух
условий события
![]() называются гипотезами по отношению к
событию А. Также, при выполнении этих
условий, очевидно выполняется равенство:
называются гипотезами по отношению к
событию А. Также, при выполнении этих
условий, очевидно выполняется равенство:
![]()
Тогда по теореме умножения имеем формулу полной вероятности:
![]() (6.11)
(6.11)
Если записать теорему умножения для события А и одной из гипотез:
![]()
то получаем формулу Байеса:
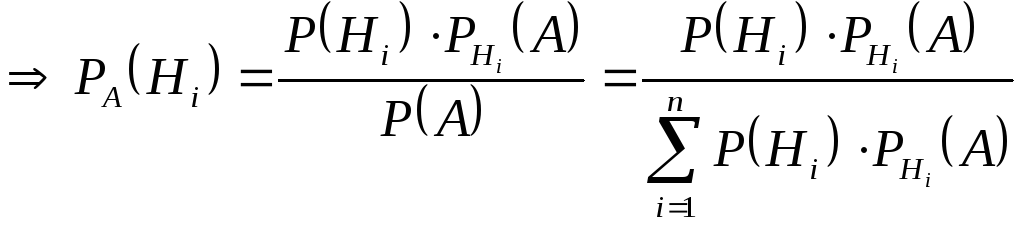 (6.12)
(6.12)
На практике возможна ситуация, при которой известно, что событие А произошло, но не известно какая из гипотез произошла. В этом случае вероятности гипотез могут быть пересчитаны по формуле Байеса.
-
Дискретные случайные величины и их характеристики.
Дискретной случайной величиной (ДСВ) называется такая случайная величина, которая может принимать значения из некоторого упорядоченного по возрастанию списка значений (конечного или бесконечного).
Дискретная случайная величина (ДСВ) описывается рядом распределения, который представляет собой таблицу с указанием всех возможных значений этой ДСВ в возрастающем порядке и вероятностей принятия каждого из этих значений. Сумма всех вероятностей должна быть равна единице, так как принятие этой ДСВ одного из значений, указанных в ряде распределения есть достоверное событие. Ряд распределения выглядит как такая таблица:
|
X |
pi |
|
X1 |
P1 |
|
X2 |
P2 |
|
. |
. |
|
. |
. |
|
xn |
pn |
Таблица может быть и бесконечной.
Должно выполняться
![]() .
i=1,2,…
и так далее. (8.3)
.
i=1,2,…
и так далее. (8.3)
Здесь и далее суммирование по всем возможным значениям ДСВ (по всем строкам таблицы).
Индикатором события А называется случайная величина , равная единице, если в результате опыта событие А произошло, и – нулю, если не произошло
Таким образом, можно сделать вывод, что для ДСВ функция распределения есть ступенчатая функция, непрерывная слева.
Действительно, в точках разрыва значение функции есть значение нижней точки на разрыве, следовательно, в этой точке функция непрерывна слева, а справа разрывна. В остальных точках функция просто непрерывна, следовательно непрерывна и слева и справа. Накопленная вероятность есть вероятность в ряде распределения «плюс все предыдущие вероятности» в этом ряде. Поэтому ряд распределения, вместе с накопленной вероятностью, равной функции распределения, для рассматриваемой ДСВ можно записать так:
Последнее значение (если ряд распределения конечный, как в данном случае) равно единице.
19. Непрерывные случайные величины и их характеристики.
Для НСВ невозможно написать ряд распределения. Действительно, между любыми двумя числами существует сколь угодно много других действительных чисел, поэтому все числа из некоторого промежутка выписать в возрастающем порядке (и ни в каком другом) невозможно. НСВ характеризуется функцией плотности:
![]() (8.11)
(8.11)
В
других источниках функцию плотности
часто обозначают
![]() .
.
Функция плотности обладает следующими свойствами:
-
 - Функция плотности
всюду неотрицательная. Это свойство
следует из неубывания функции
распределения.
- Функция плотности
всюду неотрицательная. Это свойство
следует из неубывания функции
распределения. -
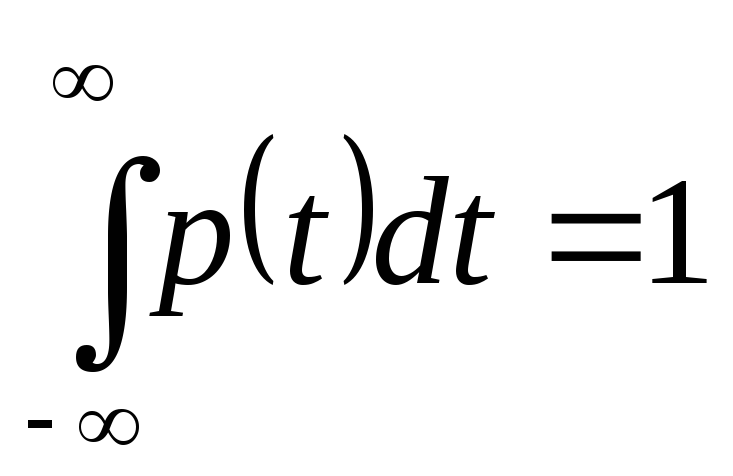 .
(8.12)
.
(8.12)
Это свойство непосредственно вытекает из (8.11).
-
 .
Это свойство вытекает из предыдущего.
Действительно, если бы не выполнялось
свойство 3), то несобственный интеграл
в (8.12) был бы расходящимся. Противоречие
доказывает свойство.
.
Это свойство вытекает из предыдущего.
Действительно, если бы не выполнялось
свойство 3), то несобственный интеграл
в (8.12) был бы расходящимся. Противоречие
доказывает свойство. -
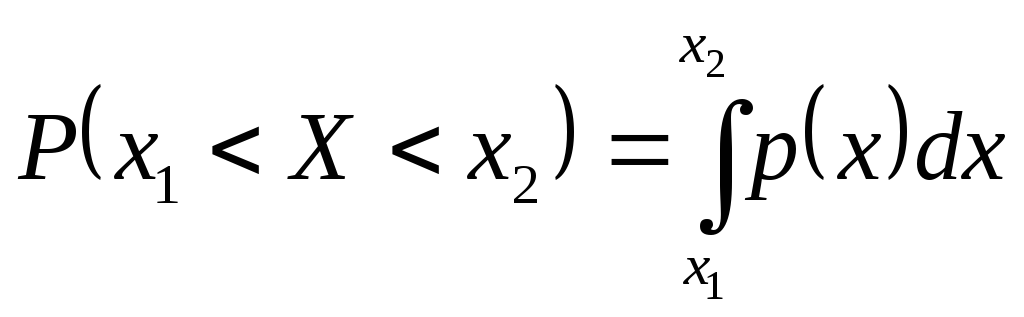 Это свойство
вытекает из (8.2) и из формулы Ньютона-Лейбница
(см математический анализ, определенный
интеграл). С учетом (8.2) можно записать:
Это свойство
вытекает из (8.2) и из формулы Ньютона-Лейбница
(см математический анализ, определенный
интеграл). С учетом (8.2) можно записать:
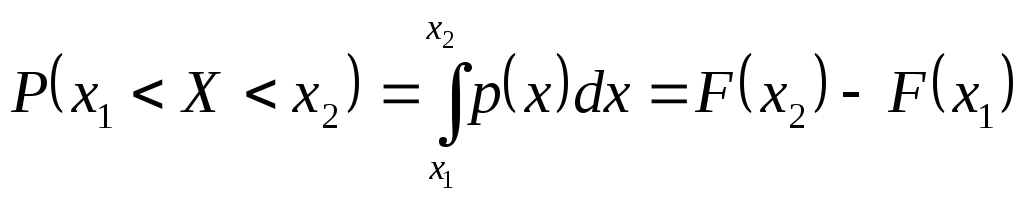 (8.13)
(8.13)
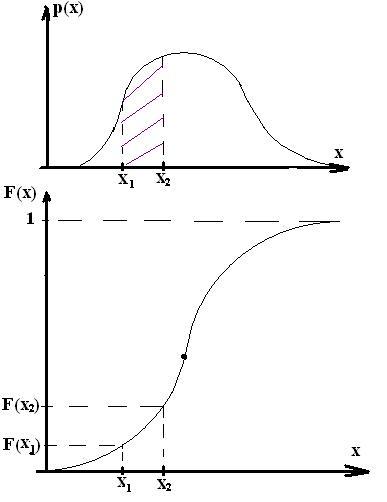
Связь между функцией распределения и функцией плотности можно представить на рисунке. Рассмотрим некоторую ДСВ, у которой функция плотности и функция распределения которой такие, как изображены на рисунке:
-
Вероятность попадания случайной величины в пределы заданного участка.
Зная функцию F(x) , вычислим вероятность того, что случайная величина примет значение заключенное в интервале (a;b). Пользуясь теоремой сложения вероятностей запишем вероятность того, что х<b будет складываться из вероятностей Р(х<b)=Р(х<a)+Р(а£х). Выразим Р(а£х<b)=Р(х<b)-P(x<a)=F(b)-F(a). Таким образом искомая вероятность равна приращению функции распределения на данном интервале.
Отдельная вероятность попадания в точку. Полученную формулу нахождения вероятностей используем для х=а при условии, что
![]()
Свойства функции распределения
-
 непрерывна
справа[1]
непрерывна
справа[1]
![]()
-
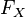 не
убывает
на всей числовой прямой.
не
убывает
на всей числовой прямой. -
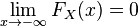 .
. -
 .
.
-
Распределение случайной величины
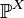 однозначно
определяет функцию распределения.
однозначно
определяет функцию распределения.
-
Верно и обратное: если функция
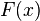 удовлетворяет
четырём перечисленным выше свойствам,
то существует вероятностное пространство
и определённая на нём случайная
величина, такая что
удовлетворяет
четырём перечисленным выше свойствам,
то существует вероятностное пространство
и определённая на нём случайная
величина, такая что
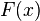 является
её функцией распределения.
является
её функцией распределения.
-
-
По определению непрерывности справа, функция
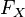 имеет
правый
предел
имеет
правый
предел
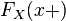 в
любой точке
в
любой точке
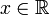 ,
и он совпадает со значением функции
,
и он совпадает со значением функции
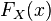 в
этой точке.
в
этой точке.
-
В силу неубывания, функция
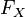 также
имеет и левый предел
также
имеет и левый предел
 в
любой точке
в
любой точке
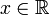 ,
который может не совпадать со значением
функции. Таким образом, функция
,
который может не совпадать со значением
функции. Таким образом, функция
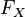 либо
непрерывна в точке, либо имеет в ней
разрыв
первого рода.
либо
непрерывна в точке, либо имеет в ней
разрыв
первого рода.
-
21. Начальный момент первого порядка называется математическим ожиданием EX этой случайной величины:
![]() (8.5)
(8.5)
Из формулы видно, что математическое ожидание есть средневзвешенное по вероятности значение случайной величины.
Центральный момент второго порядка называется дисперсией DX этой случайной величины:
![]() (8.7)
(8.7)
Дисперсия характеризует разброс возможных значений СВ относительно математического ожидания. Дисперсию можно вычислить и по другой формуле:
![]() .
(8.8)
.
(8.8)
Свойства математического ожидания и дисперсии.
-
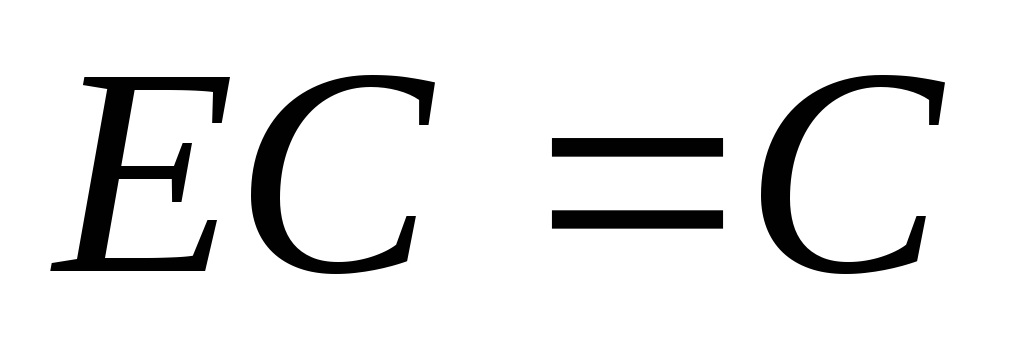 ,
где С – константа. То есть математическое
ожидание константы равно самой константе.
,
где С – константа. То есть математическое
ожидание константы равно самой константе.
Доказательство. Константу С можно представить как ДСВ с таким рядом распределения:
|
X |
Pk |
|
C |
1 |
Но
тогда по определению
![]() , что и требовалось доказать.
, что и требовалось доказать.
-
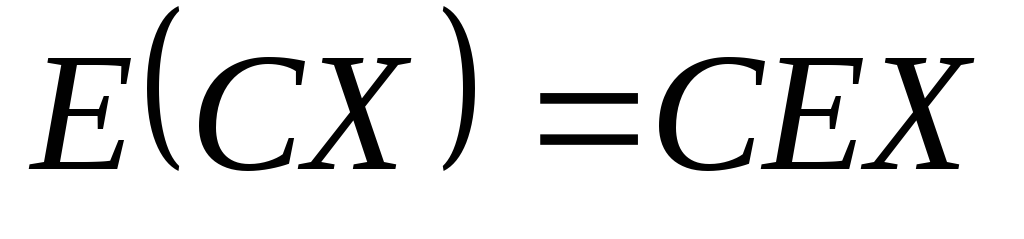 То есть постоянный
множитель можно выносить за знак
математического ожидания. Это свойство
вытекает из аналогичных свойств суммы
и интеграла.
То есть постоянный
множитель можно выносить за знак
математического ожидания. Это свойство
вытекает из аналогичных свойств суммы
и интеграла.
-
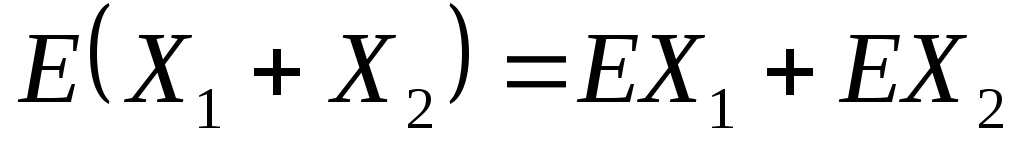 То есть математическое
ожидание суммы двух (или нескольких)
СВ равно сумме их математических
ожиданий.
То есть математическое
ожидание суммы двух (или нескольких)
СВ равно сумме их математических
ожиданий.
-
 .
То есть дисперсия константы равна
нулю. Доказательство этого свойства
очень простое и здесь не приводится.
Смысл этого свойства в том, что константа
не может иметь «отклонений» или
«разброса».
.
То есть дисперсия константы равна
нулю. Доказательство этого свойства
очень простое и здесь не приводится.
Смысл этого свойства в том, что константа
не может иметь «отклонений» или
«разброса». -
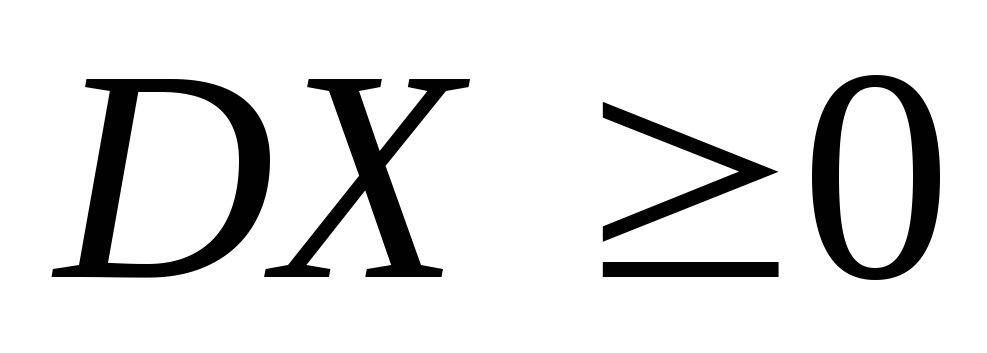 . То есть дисперсия
не может быть отрицательной. Это прямо
вытекает из определения дисперсии.
. То есть дисперсия
не может быть отрицательной. Это прямо
вытекает из определения дисперсии. -
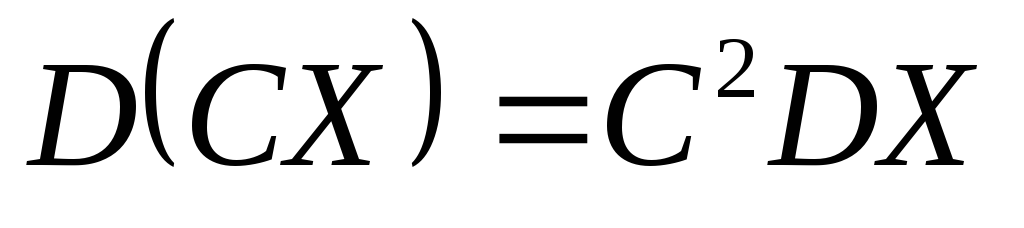 .
То есть постоянный множитель можно
выносить за знак дисперсии «в квадрате».
Это также вытекает из определения
дисперсии.
.
То есть постоянный множитель можно
выносить за знак дисперсии «в квадрате».
Это также вытекает из определения
дисперсии. -
Если СВ
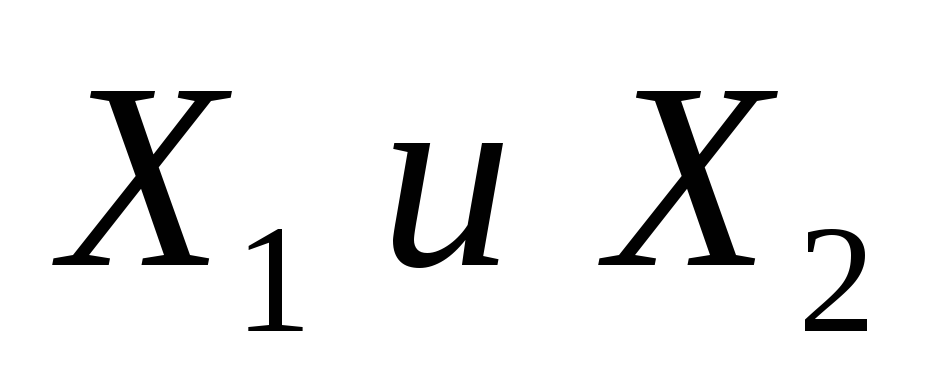 независимы, то
независимы, то
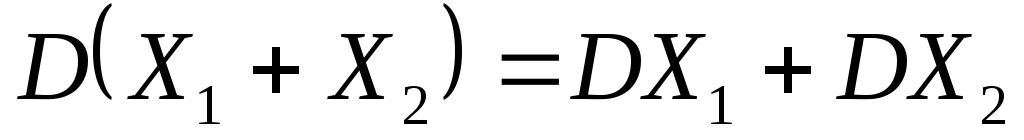 .
То есть для независимых СВ дисперсия
суммы двух (или нескольких) СВ равна
сумме их дисперсий. Отметим, что
аналогичное свойство математического
ожидания 3) выполняется для любых СВ.
.
То есть для независимых СВ дисперсия
суммы двух (или нескольких) СВ равна
сумме их дисперсий. Отметим, что
аналогичное свойство математического
ожидания 3) выполняется для любых СВ. -
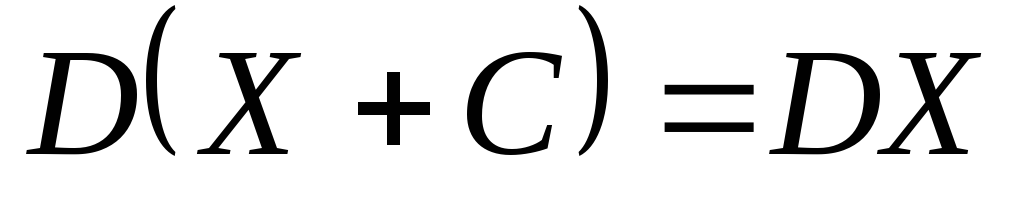 .
То есть дисперсия не зависит от сдвига.
Это свойство прямо вытекает из свойств
4 и 7. Смысл этого свойства понятен:
разброс зависит от формы кривой графика
плотности распределения, но не зависит
от положения этой кривой на оси х.
.
То есть дисперсия не зависит от сдвига.
Это свойство прямо вытекает из свойств
4 и 7. Смысл этого свойства понятен:
разброс зависит от формы кривой графика
плотности распределения, но не зависит
от положения этой кривой на оси х.
22. (+ конец 21)Начальный момент первого порядка называется математическим ожиданием EX этой случайной величины:
![]() (8.15)
(8.15)
Из формулы видно, что математическое ожидание есть средневзвешенное по вероятности значение случайной величины.
Центральным моментом порядка k называется неслучайная величина
![]() (8.16)
(8.16)
Центральный момент второго порядка называется дисперсией DX этой случайной величины:
![]() (8.17)
(8.17)
Дисперсия характеризует разброс возможных значений СВ относительно математического ожидания. Дисперсию можно вычислить и по другой формуле:
![]() .
(8.18)
.
(8.18)
Среднеквадратичное
отклонение вычисляется также как и для
ДСВ
![]() .
.
23. Биномиальное распределение.
Пусть имеется n независимых испытаний (опытов), в каждом из которых может произойти событие А с вероятностью p (в каждом опыте одинаковая вероятность). Наступление события А назовем успехом. Рассматривается ДСВ X - количество успехов в этих n испытаниях. Величина q=1-p, очевидно, есть вероятность неуспеха. Очевидно, что X может принимать любые целые значения от 0 до n. Ряд распределения запишется так:
|
|
|
|
0 |
|
|
1 |
|
|
2 |
|
|
… |
… |
|
n |
|
Математическое
ожидание
![]() .
Дисперсия
.
Дисперсия
![]() .
.
Доказательство. Рассмотрим n независимых событий:
![]() = в первом испытании
наступил успех,
= в первом испытании
наступил успех,
![]() = во втором испытании наступил успех,
и так далее …
= во втором испытании наступил успех,
и так далее …
![]() = в n-ом
испытании наступил успех. Вероятность
каждого из этих событий по условию
испытаний равна p. Очевидно, что
= в n-ом
испытании наступил успех. Вероятность
каждого из этих событий по условию
испытаний равна p. Очевидно, что
![]() .
Действительно, если в первом испытании
наступил успех, то
.
Действительно, если в первом испытании
наступил успех, то
![]() ,
иначе
,
иначе
![]() .
То же можно сказать и для любого другого
испытания. Таким образом, сумма индикаторов
.
То же можно сказать и для любого другого
испытания. Таким образом, сумма индикаторов
![]() есть количество успехов в этих испытаниях,
то есть это и есть X.
Но тогда математическое ожидание
есть количество успехов в этих испытаниях,
то есть это и есть X.
Но тогда математическое ожидание
![]() есть сумма математических ожиданий
индикаторов (по свойству математического
ожидания), а математическое ожидание
индикатора события равно вероятности
этого события, и мы получаем:
есть сумма математических ожиданий
индикаторов (по свойству математического
ожидания), а математическое ожидание
индикатора события равно вероятности
этого события, и мы получаем:
![]() .
Точно так же доказывается формула для
дисперсии. В последнем случае используется
независимость событий
.
Точно так же доказывается формула для
дисперсии. В последнем случае используется
независимость событий
![]() ,
,
![]() ,…
,…![]() .
.
