Теорема.

Если  - интегрирующий множитель уравнения вида (1), а функция  такая, что

.

Тогда , где  - произвольная дифференцируемая функция, также будет интегрирующим множителем того же уравнения.

Это свойство интегрирующего множителя позволяет во многих случаях находить его методом разбиения данного уравнения на две части.

Пусть  - общие интегралы и интегрирующие множители соответственно для уравнений

.

Тогда, в силу приведенной выше теоремы, функции

являются интегрирующими множителями для первого и второго уравнения соответственно. Если удастся подобрать функции так, чтобы выполнялось равенство

,

то интегрирующим множителем для уравнения

,

очевидно, является функция

.

Пример 5. Решить уравнение .

Решение.

Для отыскания интегрирующего множителя воспользуемся методом разделения уравнения на два:

.

Нетрудно установить, что интегрирующие множители этих уравнений. а также их интегралы имеют вид:

,

Согласно указанному методу, интегрирующий множитель данного уравнения ищем из соотношения

.

Отсюда

.

Полагая здесь , получаем

,

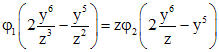или

.

Пусть . Тогда

.

Следовательно,

.

Заметим, что для  аналогично можно найти

.

В обоих случаях после интегрирования уравнения в полных дифференциалах и упрощений получаем ответ

.

8. Комплексные числа

Комплексные числа являются расширением множества действительных чисел. В результате расширения множества действительных чисел было введено понятие мнимой единицы , которая существует на множестве комплексных чисел, но не существует на множестве действительных

теорема алгебры:

На поле комплексных чисел многочлен степени n имеет ровно n корней, если каждый корень считать столько раз, какова его кратность.

Можно показать, что если число является корнем многочлена (с действительными коэффициентами), то сопряженное число также является корнем этого многочлена.

Пример: многочлен имеет два различных сопряженных корня: и . Из этого следствия можно сделать вывод о том, что многочлен нечетной степени всегда имеет хотя бы один действительный корень, так как комплексные корни в списке корней присутствуют сопряженными парами.

9. Линейные дифференциальные уравнения с постоянными коэффициентами

Определение линейных дифференциальных уравнений с постоянными коэффициентами. Определение однородных и неоднородных линейных дифференциальных уравнений с постоянными коэффициентами. Рассмотрены свойства их решений.

Линейное дифференциальное уравнение с постоянными коэффициентами – это уравнение вида a₀ y⁽ⁿ⁾ + a₁ y^(n-1) + ... + a_n-1 y' + a_n y = f(x);    a_i = const;   a₀ ≠ 0

Линейное однородное дифференциальное уравнение с постоянными коэффициентами – это уравнение вида a₀ y⁽ⁿ⁾ + a₁ y^(n-1) + ... + a_n-1 y' + a_n y = 0;    a_i = const;   a₀ ≠ 0

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами – это уравнение вида a₀ y⁽ⁿ⁾ + a₁ y^(n-1) + ... + a_n-1 y' + a_n y = f(x);    f(x) ≠ 0;   a_i = const;   a₀ ≠ 0

Здесь все коэффициенты a_i - постоянные. n - порядок уравнения. Член f(x) называется неоднородной частью уравнения.

Свойства решений линейных дифференциальных уравнений с постоянными коэффициентами

Однородные уравнения

Рассмотрим линейное однородное дифференциальное уравнение:

(1)

Общее решение такого уравнения можно записать в виде:

где y₁, y₂, ... y_n-1, y_n - линейно независимые частные решения уравнения (1). Каждое из них удовлетворят уравнению (1):

В этом случае говорят, что функции y₁, y₂, ... y_n-1, y_n образуют фундаментальную систему решений линейного однородного уравнения (1).

Фундаментальная система решений линейного однородного уравнения (1) – это n линейно независимых функций y₁(x), y₂(x), ... y_n-1(x), y_n(x), каждая из которых является решением уравнения (1).

Линейно независимые функции y₁(x), y₂(x), ... y_n-1(x), y_n(x) – это такие функции, для которых соотношение: α₁ y₁(x) + α₂ y₂(x) + ... + α_n-1 y_n-1(x) + α_n y_n(x) = 0 может выполняться только если все постоянные α₁, α₂, ..., α_n-1, α_n равны нулю.

Линейно зависимые функции y₁(x), y₂(x), ... y_n-1(x), y_n(x) – это функции, между которыми имеет место линейная зависимость: α₁ y₁(x) + α₂ y₂(x) + ... + α_n-1 y_n-1(x) + α_n y_n(x) = 0 где α₁, α₂, ..., α_n-1, α_n - постоянные, из которых хотя бы одна отлична от нуля.

Неоднородные уравнения

Рассмотрим линейное неоднородное дифференциальное уравнение:

(2)

Пусть Y - частное решение этого уравнения. Тогда общее решение уравнения (2) равно сумме общего решения однородного уравнения плюс частное решение неоднородного:

Здесь

- общее решение однородного уравнения:

Y- частное (любое) решение неоднородного уравнения:

 

Часто встречается случай, когда неоднородная часть f(x) может быть представлена в виде суммы функций:

Тогда частное решение Y также может быть представлено в виде суммы частных решений:

каждое из которых удовлетворяет уравнению с правой частью в виде одной из функций f_i(x):

В некоторых случаях бывает легче решать отдельные частные решения от более простых неоднородных частей, а затем получать частное решение для всего уравнения суммированием полученных частных решений.