7 Вопрос.

Уравнения в полных дифференциалах. Интегрирующий множитель.

Уравнение

                                                                                                                          (1)

называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции , т.е.

.

Теорема.

Если функции  непрерывны в некоторой односвязной области , то условие

является необходимым и достаточным для того, чтобы выражение

было полным дифференциалом функции .

Если известна функция, полным дифференциалом которой является левая часть  уравнения (1), то все решения этого уравнения имеют вид , где - произвольная постоянная.

Чтобы найти функцию  нужно воспользоваться равенствами

                                                                 .                                                    (2)

Интегрируя первое из этих равенств по x, определим функцию  с точностью до произвольной дифференцируемой функции переменного y:

                                                           ,                                              (3)

где  - произвольная дифференцируемая функция. Функция , такая что . Дифференцируя (3) по y, с учетом второго равенства из (2) получаем уравнение для определения :

.

Пример 1. Решить уравнение .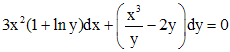

Решение.

Так как

во всех точках полуплоскости , то данное уравнение является уравнением в полных дифференциалах. Найдем функцию  такую, что

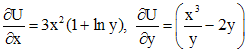                                                         .                                                   (4)

Проинтегрировав первое равенство из (4) по x, получим:

.

Для нахождения  продифференцируем по y полученное соотношение и подставим во второе равенство (4):

.

Тогда  откуда,  . Значит .

Решение данного уравнения запишется в виде:

.

Для интегрирования уравнений вида (1) иногда применяют метод, состоящий в выделении полных дифференциалов из разных групп слагаемых, стоящих в левой части уравнения. Для выделения полных дифференциалов используют формулы:

Пример 2. Решить уравнение .

Решение.

Заметим, что в правой части уравнения стоит функция, зависящая от частного , а в левой - выражение, похожее на дифференциал частного. Поэтому, разделив обе части данного уравнения на , получим:

.

Обозначим . Тогда полученное уравнение можно записать в виде:

.

Разделяя переменные, будем иметь:

.

Проинтегрировав, ответ запишем в виде:

.

Конечно, не всякое дифференциальное уравнение вида (1) является уравнением в полных дифференциалах. Всегда можно привести его к уравнению такого типа умножением на некоторую не равную нулю функцию , называемуюинтегрирующим множителем. Но не всегда легко найти такую функцию.

Если  интегрирующий множитель уравнения (1), уравнение

является уравнением в полных дифференциалах:

,

т.е. интегрирующий множитель есть решение уравнения

                                                      .                                                        (5)

Найти функцию  из уравнения (5) в общем случае довольно сложно. В частных случаях соотношение (5) значительно упрощается.

Случай 1. Если уравнение (1) имеет интегрирующий множитель, зависящий только от x, т.е. , то из (5) имеем

.

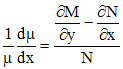Случай 2. Если уравнение (1) допускает интегрирующий множитель как функцию одной переменной y, т.е. , то

.

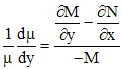Случай 3. Если уравнение (1) имеет интегрирующий множитель вида , где  - известная функция, то

.

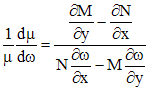Пример 3. Решить уравнение .

Решение.

Очевидно, что данное уравнение не является уравнением в полных дифференциалах. Попытаемся найти интегрирующий множитель . Поскольку выражение

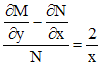
не зависит от y, то уравнение для определения  примет вид

.

Данное уравнение является уравнением с разделяющимися переменными одним из решением которого, является функция . Умножая обе части исходного уравнения на интегрирующий множитель , получаем уравнение в полных дифференциалах:

.

Интегрируя его, находим общее решение:

.

Пример 4. Решить уравнение .

Решение.

Очевидно, найти интегрирующий множитель, зависящий только от одной переменной нельзя. Будем искать интегрирующий множитель в виде . Пусть , тогда уравнение для нахождения  примет вид

,

интегрируя, которое находим

.

Умножая обе части исходного уравнения на данный интегрирующий множитель, получаем уравнение в полных дифференциалах:

.

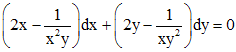Интегрируя полученное уравнение, находим общее решение:

.