Лабораторный практикум по физике

Таким образом, в результате совместного действия квазиупругой силы и силы трения система совершает колебательное движение, амплитуда которого условно принимается равной

т. е. убывает с течением времени по экспоненциальному закону. Значит, в системе возникают затухающие колебания, частота ω которых, как видно из (12), зависит не только от параметров системы m и k, но и от коэффициента γ, характеризующего силу вязкого трения. Очевидно, что

от времени. Однако, трение замедляет движение, увеличивая при этом период и уменьшая частоту. Поэтому затухающие колебания не являются периодическими. Отсюда логично следовало бы называть T и ω условным периодом и условной частотой. Величина δ характеризует быстроту затухания колебаний и называется коэффициентом затухания. Возьмем отношение двух амплитуд (13), разделенных во времени интервалом в одну секунду

Так как δ = γ/2m = const для данной системы, то выражение (16) показывает, что отношение двух амплитуд, разделенных интервалом в одну секунду, всегда одно и то же. Удобно пользоваться так называемым логарифмическим декрементом затухания. Эта величина равна логарифму отношения двух последовательных амплитуд, разделенных промежутком времени, равным периоду

21

Таким образом, логарифмический декремент затухания в T раз больше, чем коэффициент затухания. Так как δ и T постоянны, то и Θ = const. А это означает, что отношение двух амплитуд, отстоящих во времени на один период, постоянно и не зависит от выбора момента времени t. Для нахождения коэффициента затухания δ поступают следующим образом. Измеряют время t , в течение которого амплитуда А меняется, например, в два раза. Тогда из (13) имеем

A = A20 = A0 · e−δt.

После логарифмирования получим искомое выражение для δ

2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Экспериментальная установка представляет собой набор пружин, подвешенных на штативе. Схема ее аналогична изображенной на рисунке 1, с тем различием, что пружины располагаются вертикально. Измерения проводятся в следующем порядке.

1.Определите коэффициент упругости для каждой пружины по формуле k = P/x по методике, изложенной в работе № 1, используя набор различных грузов весом P . Для этого сначала измерьте вес грузов, затем, подвешивая их к пружине, найдите смещение x.

2.Убедитесь в справедливости формулы (5). Для этого вычислите пе-

риод T0 , используя значение k (для одной из пружин), полученное в п. 1 для грузов с различными массами m. Сравните полученные результаты с экспериментально определяемыми периодами. Для этого измерьте секундомером время 10–15 полных колебаний (не менее трех раз) и най-

где t – время N полных колебаний.

3. Определите зависимость периода собственных колебаний пружинного маятника от коэффициента упругости пружины. Для этого измерьте периоды T0 собственных колебаний пружин при одном и том же грузе P и постройте график зависимости T02 от 1/k (по оси абсцисс отложите значения 1/k).

22

4. Вычислите коэффициент упругости k одной из пружин по формуле

которая получается из (5). Для этого необходимо определить по экспериментальной формуле периоды T01 и T02 для грузов с массами m1 и m2

.Полученный результат сравните с данными п. 1.

5.Определите логарифмический декремент затухания пружинного маятника по следующей методике.

Поместите один из грузов на пружине в сосуд с водой и определите период его колебаний T по формуле (19). Выводя груз из положения

равновесия и отмечая его начальное отклонение, равное A0, определите время t, в течение которого амплитуда его колебаний уменьшится в два раза. Измерения повторите несколько раз при разных значениях отклонений. Логарифмический декремент затухания можно вычислить по формуле (17) с учетом (18)

3. КОНТРОЛЬНЫЕ ВОПРОСЫ

r

1. Покажите, что период колебаний T0 = 2π mk .

2.Найдите закон движения груза на пружине в поле тяжести.

3.Докажите, что свободные незатухающие колебания являются гармоническими.

4.Выведите период колебаний математического маятника.

5.Начертите график зависимости амплитуды от времени в вязкой

среде.

6.Определите относительное изменение амплитуд при малом значении Θ.

Библиографический список

1.Иверонова В.И. Механика и молекулярная физика: Физический практикум. – М.: Наука, 1967. – С. 156.

2.Лабораторный практикум по физике /Под ред. А.С.Ахматова. – М.: Высшая школа. 1980. – С. 177.

3.Савельев И.В. Курс общей физики. – М.: Наука, 1986, т.1. – 432 с.

23

Лабораторная работа № 4 ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ РАЗЛИЧНЫХ

ТЕЛ МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ

Цель работы: Определение моментов инерции твердых тел.

Оборудование: Трифилярный подвес, рулетка, линейка, секундомер, набор тел.

1. КРАТКАЯ ТЕОРИЯ

Рассмотрим крутильные колебания диска, подвешенного на упругой нити (рис. 1). Момент сил упругости M , возникающих при закручивании нити и стремящихся вернуть диск в исходное положение, пропорционален углу поворота диска α

где k – постоянный коэффициент, называемый модулем кручения, зависящий от свойств нити. Знак минус выбран потому, что упругий момент нити направлен в сторону, противоположную положительному направлению отклонения диска. Работа, затрачиваемая при закручивании нити, перейдет в потенциальную энергию деформированной нити. В дальнейшем энергия кручения превратится в кинетическую энергию вращательного движения

Рис. 1.

диска. В момент прохождения положения равновесия кинетическая энергия примет максимальное значение, а диск будет продолжать двигаться по инерции в направлении, противоположном первоначальному. Если пренебречь незначительными потерями энергии на трение, то можно наблюдать в дальнейшем превращение энергии вращательного движения вновь в потенциальную энергию деформированной нити и обратный переход ее в кинетическую. Таким образом, установятся гармонические крутильные колебания системы относительно оси, проходящей через центр инерции (тяжести) диска. Для однородного диска этот центр совпадает с геометрическим. Действительно, если момент инерции диска относительно оси, проходящей через центр и совпадающей с нитью

24

равен J , то записав основное уравнение динамики для вращательного движения с учетом (1), для круговой частоты колебаний получим вы-

p

ражение ω0 = k/J. Угол отклонения от положения равновесия (угол поворота) будет изменяться в зависимости от времени по закону синуса или косинуса. Например,

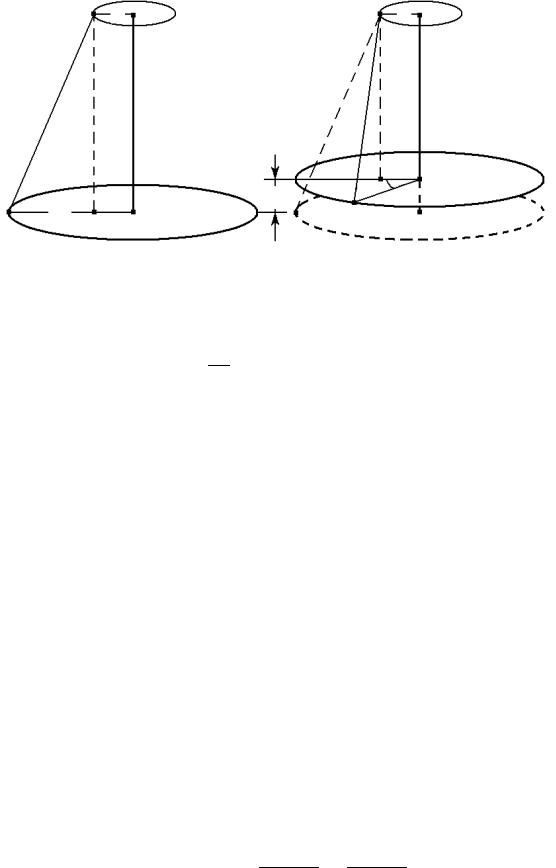
чение k часто неизвестно, поэтому момент инерции можно определить по другой методике, например, с использованием трифилярного подвеса. Он представляет из себя два диска разных радиусов R и r, скрепленных между собой тремя нерастяжимыми нитями длиной l (рис. 2 и рис. 3 а, б).

где m – масса платформы нижнего диска. При крутильных колебаниях эта энергия будет переходить в кинетическую энергию вращательного движения Eкин. В момент прохождения положения равновесия (α = 0), Eкин станет максимальной, а потенциальная – равной нулю. Если не происходит потери энергии, то на основании закона сохранения энергии будем иметь

где максимальное значение угловой скорости диска ωmax можно найти,

25

Рис. 3.

взяв производную от угла (2) по времени

dα

ω = dt = ω0 · α0 · cos ω0t .

Поскольку ω0 = 2π/T , а максимальное значение косинуса равно единице, то будем иметь

Зная m и ωmax из (4) можно определить искомый момент инерции J , для чего необходимо лишь найти h.

Расстояние между дисками h1 в исходном положении определяется из рисунка 3а по теореме Пифагора. Обозначив BD = r, AF = R − r,

При повороте нижнего диска на угол α0 согласно рисунка 3б рассто-

26

Подставляя в (8) левые части из (6) и (7) для h получим выражение

Для малых углов, когда sin2(α0/2) ≈ α02/4 выражение (9) можно представить в виде

Подставляя в уравнение (4) величины h и ωmax согласно (5) и (10) для искомого момента инерции J получим выражение

С помощью (11) можно вычислить требуемые моменты инерции тел, если известны геометрические параметры, характеризующие систему (величины l, R, r), платформы, а также период T крутильных колебаний.

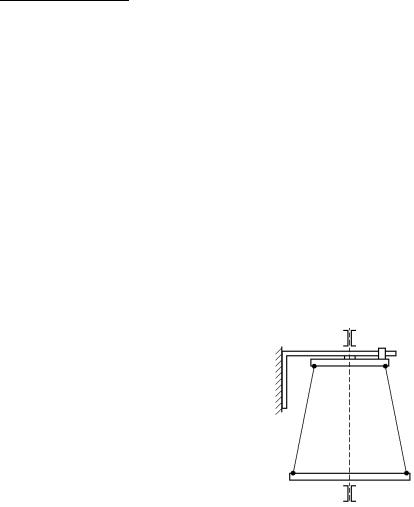
Схема экспериментальной установки показана на рисунке 4.

Нижний массивный диск I (платформа) крепится

на трех симметрично расположенных металлических нитях к верхнему диску II меньшего радиуса и может поворачиваться вокруг оси O0O00. Верхний диск крепится кронштейном K к стене. Однако, за счет стопора P сам он неподвижен, а вращается нижний диск. В результате все три нити при этом принимают наклонное положение и возникает момент сил, стремящийся вернуть нижний диск в положение равновесия. Возникают крутильные колебания, период которых, как мы видели ранее, будет зависеть от момента инерции диска.

Работа выполняется в следующем порядке:

1. Не нагружая нижней платформы, проверьте, пригодна ли установка для измерений, то есть, нормально ли функционирует устройство для

27

возбуждения крутильных колебаний, не возникают ли при этом побочные маятникообразные движения платформы.

2.Определите период колебаний T не загруженной платформы по формуле T = t/N , где t – время 10–15 колебаний платформы, N – число этих колебаний. Добейтесь того, чтобы период T не зависел от

амплитуды крутильных колебаний α0. Для данной установки это выполняется при α0 ≤ 5 − 10◦.

3.Определите момент инерции J0 ненагруженной платформы, используя соотношение (11). Масса платформы m указана на установке, период колебаний T измеряется секундомером.

4.Рассчитайте момент инерции Ji каждого из грузов, имеющих форму цилиндров, по формуле

где масса mi, указана на установке, а радиус основания цилиндра ri измеряется линейкой. Сложив момент инерции Ji с измеренным моментом инерции платформы J0, проверьте справедливость соотношения J = J0 + Ji, где момент инерции платформы J следует вычислить по формуле (4), определив предварительно период колебаний T платформы с каждым из грузов mi. Тела на платформу следует класть так, чтобы не было перекоса платформы.

5. Вычислите момент инерции платформы с двумя телами J = J0 + J1 + J2, поместив цилиндры в центре друг на друга. Убедитесь в справедливости соотношения

X

J = J0 + miri2/2 .

i

3.КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Покажите, что выражение (2) является решением основного уравнения динамики J α¨ + kα = 0.

2.При каких упрощающих предположениях выведена формула (11)?

3.Какие факторы ограничивают точность опытов?

4.Можно ли пользоваться предложенным методом для определения моментов инерции тел в том случае, если ось вращения платформы не проходит через их центр тяжести?

5.Рассчитайте момент инерции платформы J0 по формуле для сплошного диска (цилиндра). Параметры платформы – радиус R и ее масса m

28

– указаны на установке. Данный результат сравните с экспериментальным, полученным по формуле (4) в соответствии с п.3.

Библиографический список

1.Сивухин Д.В. Общий курс физики. Механика. – М.: Наука, 1979. §35-36.

2.Савельев И.В. Курс общей физики. Т 1. Механика, колебания и волны, молекулярная физика. – М.: Наука, 1989. §31-33.

3.Физический практикум. Механика и молекулярная физика под ред. Ивероновой В.И. – М.: Наука, 1967. – С. 95-98.

Лабораторная работа № 5 ИЗУЧЕНИЕ СВЯЗАННЫХ КОЛЕБАНИЙ

Цель работы: Изучение основных характеристик колебательных систем с двумя степенями свободы.

Оборудование: Секундомер, металлические стержни, тела, упругая пружина.

1. КРАТКАЯ ТЕОРИЯ

Если положение колебательной системы в любой момент времени может быть определено единственной координатой, то говорят, что система имеет одну степень свободы. Например, математический маятник, колеблющийся в заданной плоскости. В этом случае координатой может слу-

29

мер координаты x и y, характеризующие смещения вдоль соответствующих осей. Таким же образом будет происходить движение тела, закрепленного на двух парах одинаковых по жесткости пружин (плоский пружинный маятник), расположенных взаимно перпендикулярно. В приведенных примерах при малых амплитудах колебания обоих маятников будут гармоническими, т.е. смещения от положения равновесия описываются соотношением типа (1). Однако, если жесткости пружин вдоль рассмотренных направлений неодинаковы, то и частоты, с которыми происходят колебания, также различны. Эти частоты носят название нормальных частот или частот связи. Гармонические колебания, соответствующие этим частотам, называются нормальными колебаниями (или просто модами). В общем случае таких движений любая система имеет столько, сколько у нее степеней свободы. О совокупности частот нормальных колебаний говорят как о спектре колебаний системы. Любое свободное движение системы может быть представлено в виде суммы (суперпозиции) нормальных колебаний (мод) с определенными амплитудами и фазами. Связанные маятники (рис. 3а-3г) дают пример системы с двумя степенями свободы, где соответствующие отдельным модам колебания происходят вдоль одного направления.

Действительно, если маятники отклонить на одинаковые углы α1 = α2 в одну сторону (рис. 3б), то смещения от положения равновесия также равны x1 = x2. Соединяющая маятники пружина в любой момент времени остается не деформированной и на их колебания не влияет – происхо-

30