Головизин_Лекции / Лекция 10. Произведения векторов
.docЛекции по алгебре и геометрии. Семестр 1.
Лекция 10. Скалярное, векторное и смешанное произведения векторов.
Краткое содержание: определение и простейшие свойства скалярного произведения, свойство линейности скалярного произведения, скалярное произведение векторов в координатной форме, вычисление модуля вектора и угла между векторами, физический смысл скалярного произведения, векторное и смешанное произведения векторов и их свойства.
Глава 10. Скалярное, векторное и смешанное произведения векторов.
п.1. Скалярное произведение векторов.
Определение. Скалярным произведением двух векторов называется произведение их модулей на косинус угла между ними.
Обозначение:
.
Теорема. (Свойства скалярного произведения.)
1). Скалярное произведение подчиняется закону коммутативности:
,
.
2). Скалярное произведение двух векторов равно нулю тогда и только тогда, когда хотя бы один из векторов нулевой или векторы ортогональны:
или
или
.
3). Скалярный квадрат вектора равен квадрату его модуля:
.
4).
.
Доказательство. Все свойства очевидны из определения и их доказательства предоставляются читателям.
Теорема. (Свойство линейности скалярного произведения.)
1) Скалярное произведение дистрибутивно относительно сложения векторов:
,
.
2) Скалярный множитель можно выносить за знак скалярного произведения:
,
,
.
Доказательство. По свойству 4 предыдущей теоремы и по свойству проекции вектора на вектор (на ось) имеем:
.
Второе свойство доказывается аналогично.
Теорема доказана.
Замечание.
Скалярное произведение можно рассматривать
как числовую функцию от двух переменных,
определенную на декартовом квадрате
множества векторов
:
,
т.е.
,
.
Тогда, свойства теоремы могут быть записаны так:
1)
,
;
2)
,
,
.
Первое из этих свойств называется свойством аддитивности функции f по первому аргументу, а второе – свойством однородности по первому аргументу. Если выполняются оба свойства, то говорят, что функция f линейна по первому аргументу. Отсюда происходит и название этих свойств скалярного произведения.
В
силу коммутативности,
скалярное произведение как функция
двух переменных линейна и по второму
аргументу, т.е. справедливы еще два
свойства:
3)
,
;
4)
,
,
.
Теорема. (Скалярное произведение векторов в координатной форме.) Скалярное произведение векторов равно сумме произведений соответствующих координат.
Другими словами,
пусть
,
.
Тогда
.
(1)
Доказательство. Учитывая, что скалярное произведение ортогональных векторов равно нулю, а скалярный квадрат единичного вектора равен 1 , получаем:
,
ч.т.д.
Теорема доказана.
Следствие
1. Пусть
.
Тогда
.
Доказательство.
Эта формула нам уже известна. Здесь ее
можно получить, используя равенство
(1), в котором положим
:
,
откуда и следует доказываемая формула.
Следствие доказано.
Следствие
2. Пусть
,
.
Тогда
.
Доказательство. Очевидно.
п.2. Физический смысл скалярного произведения векторов. Работа постоянной силы.
Пусть материальная
точка перемещается под действием
постоянной силы
вдоль вектора перемещения
.
рис.1.
На
рисунке 1 сила
разложена на две ортогональные
составляющие
и
,
причем, из физики нам известно, что
работа при перемещении материальной
точки вдоль вектора
создается составляющей
и равна
.
С
другой стороны,
,
откуда получаем:
.
п.3. Векторное произведение векторов.
Определение.
Векторным произведением вектора
на вектор
называется третий вектор
,
который удовлетворяет следующим трем
условиям:
1)
и
;
2)
тройка векторов
является правоориентированной;
3)
.
рис.2.
Обозначение:
.
Из
определения следует, что, если векторы
,
и
отложить от одной точки, то
1)
вектор
перпендикулярен плоскости, в которой
лежат векторы
и
;
2)
кратчайший поворот вектора
к вектору
происходит против часовой стрелки, если
смотреть "сверху", т.е. со стороны
вектора
;
3)
длина вектора
численно равна площади параллелограмма,
построенного на векторах
и
,
как на его сторонах.
Теорема. (Свойства векторного произведения.)
1). Антикоммутативность:
,
.
2). Условие коллинеарности векторов:
.
3).
Модуль векторного произведения численно
равен площади параллелограмма,
построенного на векторах
и
,
как на его сторонах.
Доказательство.
1) Пусть
.
Рассмотрим вектор
.
Этот вектор удовлетворяет всем трем
условиям определения векторного
произведения вектора
на вектор
.
Действительно,
т.к.
и
,
то и
и
.
Далее, тройка векторов
является правоориентированной, т.е.
кратчайший поворот от вектора
к вектору
происходит против часовой стрелки, если
смотреть на плоскость, в которой лежат
векторы
и
"снизу", т.е. со стороны вектора
.
И,
наконец,
,
ч.т.д.
2)
Если один из векторов или оба равны
нулю, то они коллинеарные и их векторное
произведение равно нулевому вектору,
тут все очевидно. Пусть векторы
и
ненулевые. Тогда
или
,
а это в свою очередь равносильно тому,
что
,
ч.т.д.
3) Следует из формулы площади параллелограмма.
Теорема доказана.
п.4. Смешанное произведение векторов.
Определение.
Смешанным произведением упорядоченной
тройки векторов
называется скалярное произведение
первого вектора на векторное произведение
второго вектора на третий и обозначается
.
Теорема. (Геометрический смысл смешанного произведения.)
1) Модуль смешанного произведения трех векторов численно равен объему параллелепипеда, построенного на трех данных векторах, как на его ребрах:
.
2)
,
если тройка
– правоориентированная и
в противном случае.
Доказательство.
1) Обозначим через
объем параллелепипеда, построенного
на данных векторах, как на его ребрах.
рис.3.
Объем параллелепипеда
V равен произведению
площади основания S на
высоту Н:
.
Площадь основания
S численно равна модулю
векторного произведения:
,
а высота Н равна модулю проекции вектора
на вектор
:
.
Отсюда получаем:
,
ч.т.д.
2)
Так как
,
где
,
то знак смешанного произведения зависит
от угла
.
Если он острый, то смешанное произведение
и
,
если угол
– тупой. А это зависит, в свою очередь,
от ориентации тройки векторов
.
На рисунке 3 изображена правая тройка
векторов
.
Если смотреть со стороны третьего
вектора
,
то кратчайший поворот первого вектора
ко второму
осуществляется против часовой стрелки.
В этом случае угол
– острый и
.
Если же тройка
– левая, то конец вектора
будет лежать ниже плоскости векторов
и
(по сравнению с рис.3) и угол
будет тупым и
,
ч.т.д.
Теорема доказана.
Будем говорить,
что тройки векторов
и
получились из тройки
с помощью круговой перестановки векторов.
В первом случае третий вектор
переставляется на первое место, а векторы
и
сдвигаются вправо на второе и третье
места соответственно. Во втором случае,
первый вектор
переставляется на третье место, а векторы
и
сдвигаются влево на первое и второе
места соответственно. Заметим, что при
круговой перестановке векторов ни один
из них не остается на своем месте.
Если
же в тройке векторов меняются местами
только два вектора, а один из векторов
остается на своем месте, то такую
перестановку мы будем называть не
круговой перестановкой (или транспозицией).
Так тройки
,
,
получаются из тройки
транспозицией векторов. Так, например,
в тройке
остался на третьем месте вектор
.
Любую тройку векторов можно упорядочить 6-ю способами. Из них три тройки будут правыми и три тройки будут левыми.
Если
тройка
правая (как на рис.3), то правыми будут и
тройки полученные из нее круговой
перестановкой:
и
.
В то же время, тройка
будет левой и левой же будут тройки,
полученные из нее круговой перестановкой:
и
.
Лемма. Круговая перестановка в тройке векторов не изменяет ее ориентации, а транспозиция векторов изменяет ориентацию тройки на противоположную.
Доказательство проведите самостоятельно с использованием соответствующих картинок.
Следствие.
1)
;
2)
;
3)
.
Доказательство. 1) По модулю все эти смешанные произведения равны друг другу, т.к. параллелепипед, построенный на данных трех векторах, как его ребрах, не зависит от того, в каком порядке мы записываем его ребра и, соответственно, не изменяется его объем.
2) Знак смешанного произведения упорядоченной тройки векторов зависит от ее ориентации, которая не меняется при круговой перестановке и меняется при транспозиции, откуда и следуют доказываемые равенства.
3) Воспользуемся уже доказанным равенством, определением смешанного произведения и свойством коммутативности скалярного произведения:
.
Следствие доказано.
Теорема.
(Свойство линейности смешанного
произведения.) Для любых векторов и
справедливы следующие равенства:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
.
Иначе можно сказать, что смешанное произведение линейно по каждому своему аргументу.
Мы рассматриваем смешанное произведение как числовую функцию трех аргументов. Первые два свойства называются свойством линейности по первому аргументу, третье и четвертое – по второму аргументу и последние два – по третьему аргументу.
Доказательство. Достаточно доказать первое равенство, все остальные доказываются аналогично.
Воспользуемся определением смешанного произведения и свойством линейности скалярного произведения:
,
ч.т.д.
Теорема доказана.
Лемма. (О вычислении координат вектора.)
Пусть
.
Тогда
,
,
.
Доказательство.
Так как
,
то по теореме о скалярном произведении
векторов в координатной форме, получаем:
.
Аналогично доказываются оставшиеся
два равенства.
Лемма доказана.
Теорема. (Свойство линейности векторного произведения.)
Для любых векторов и действительных чисел справедливы следующие равенства:
1)
;
2)
;
3)
;
4)
.
Доказательство.
1) Докажем, что векторы
и
имеют равные координаты, откуда и будет
следовать их равенство. Пусть
,
.
Тогда по лемме, используя свойства линейности смешанного и скалярного произведений, получаем:
.
.
Аналогично
доказываются равенства
и
.
Оставшиеся равенства доказываются по такой же схеме.
Теорема доказана.
п.5. Смешанное и векторное произведения векторов в координатной форме.
Теорема.
Пусть
,
,
.
Тогда:
1)
;
2)
.
Доказательство. 1) Используем свойство линейности векторного произведения:
.
Далее, заметим, что векторные произведения коллинеарных векторов равны нулевому вектору:
.
Рассмотрим другие векторные произведения базисных векторов:
рис.4.
,
,
.
Эти равенства легко устанавливаются с помощью рис.4.
Отсюда
следует:
,
ч.т.д.
2) Воспользуемся только что доказанной формулой:
.
Теперь, по теореме о скалярном произведении векторов в координатной форме, получаем:
,
ч.т.д.
Теорема доказана.
Замечание. Векторное произведение часто записывают в форме определителя:
.
Разумеется это не определитель, а лишь форма записи векторного произведения. Она компактна и удобна для запоминания.
Следствие. Определитель не изменяется при круговой перестановке строк (столбцов) определителя. При транспозиции двух строк (столбцов) определитель меняет знак.
Доказательство. С одной стороны,
.
С другой стороны,
.
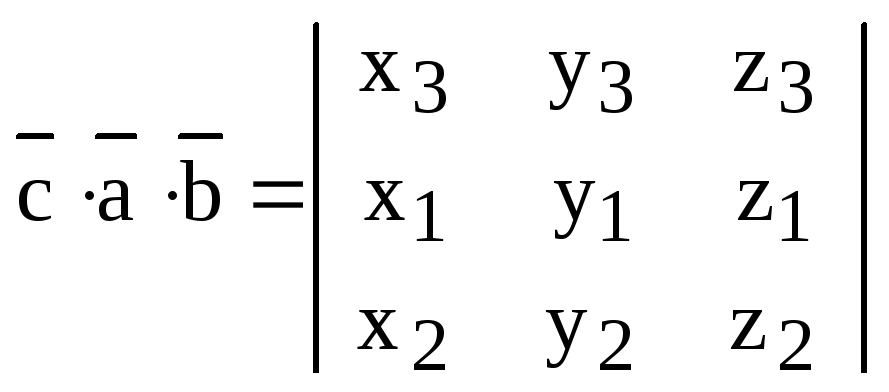Но,
,
откуда и следует утверждение. Далее,
т.к.
,
то
.
Так как определитель не изменяется при транспонировании, то доказанное свойство справедливо и для столбцов определителя.
Следствие доказано.
п.6. Некоторые приложения векторной алгебры.
Допустим, что нам дана геометрическая фигура (многоугольник, призма, пирамида) и известны координаты ее вершин. Тогда мы с помощью векторной алгебры можем находить длины сторон (ребер), углы между ними, площади многоугольников, граней призмы или пирамиды, объемы.
1) Длина стороны (ребра) АВ.
Пусть
,
.
Тогда
,
где
.
2) Угол между сторонами (ребрами) АВ и АС.
Пусть
,
,
.
Тогда
,
где
,
,
