Головизин_Лекции / Лекция 7. Полярная СК, тфкч

Лекции по алгебре и геометрии. Семестр 1.

Лекция 7. Полярная система координат. Тригонометрическая форма записи комплексных чисел.

Краткое содержание: полярная система координат на плоскости и ее связь с ПДСК, комплексная плоскость, модуль и аргумент к.ч., тригонометрическая форма записи к.ч., умножение к.ч. в тригонометрической форме записи, свойства модуля комплексных чисел.

Глава 7. Полярная система координат. Тригонометрическая форма записи комплексных чисел.

п.1. Полярная система координат на плоскости.

Определения:

Возьмем на данной плоскости произвольную точку О и назовем её полюсом. Проведем на данной плоскости из точки О направленный луч, который назовем полярным лучом. Пусть М – произвольная точка данной плоскости. Соединим точку М с полюсом отрезком прямой и назовем этот отрезок ОМ и его длину полярным радиусом точки М. Угол поворота полярного луча вокруг полюса против часовой стрелки до совпадения с полярным радиусом точки М назовем полярным углом точки М.

рис.1.

Определение. Упорядоченная пара действительных чисел называется полярными координатами точки М.

Определение. Полярной системой координат на плоскости называется полюс и полярный луч вместе с понятием полярных координат любой точки плоскости.

Замечание. Полярные координаты однозначно определяют положение любой точки на плоскости, за единственным исключением – самого полюса. Чтобы восстановить однозначность для любой точки плоскости полагают полярные координаты полюса равными нулю:

О(0; 0). Полярный угол рассматривают в пределах одного оборота и, как в тригонометрии, поворот против часовой стрелки считают положительным, а по часовой стрелке – отрицательным. Чаще всего полагают, что полярный угол .

п.2. Связь полярной системы координат с ПДСК.

Определение. Говорят, что ПДСК на плоскости Оху стандартным образом совмещена с полярной системой координат этой же плоскости, если полюс полярной системы координат совпадает с началом координат ПДСК, а полярный луч совпадает с положительной полуосью оси абсцисс Ох.

рис.2.

Положим для простоты обозначений:

. Тогда в этих обозначениях имеет место следующая теорема.

Теорема. Пусть ПДСК на плоскости Оху стандартным образом совмещена с полярной системой координат на этой же плоскости. Тогда декартовые координаты (х, у) любой точки плоскости связаны с её полярными координатами следующими соотношениями:

. (1)

Доказательство. 1-й способ. Пусть точка М лежит в первой четверти. Тогда равенства (1) следуют из прямоугольного треугольника изображенного на рис.2. Случаи других расположений точки М оставляются читателю в качестве упражнения. Не забудьте, кроме всего прочего, рассмотреть 4 случая расположения точки М на положительных и отрицательных координатных полуосях.

2-й способ. Опишем окружность единичного радиуса с центром в точке О.

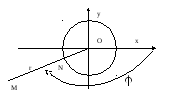
рис.3.

Пусть N – точка пересечения единичной окружности с полярным лучом ОМ (или с его продолжением, если ). Тогда – декартовые координаты точки N. Если , то и формулы (1) очевидны. Пусть . Рассмотрим отношение, в котором точка О делит отрезок MN: . Воспользуемся формулами вычисления координат точки деления отрезка:

, .

Но и , отсюда следует, что

и , ч.т.д.

Теорема доказана.

Из формул (1) легко выразить полярные координаты через декартовые. Действительно, возведя равенства (1) в квадрат и складывая, получаем: , откуда

(2)

Разделив второе уравнение на первое, получим:

, (3)

откуда можно найти полярный угол :

, если (4)

или

, если . (5)

А в какой четверти лежит полярный угол можно определить зная знаки декартовых координат х и у.

Заметим, что если полярный угол лежит в первой или четвертой четверти: , то его можно выразить через арксинус:

и . (6)

Если полярный угол лежит в первой или второй четверти: , то его можно выразить через арккосинус:

и . (7)

Если же если полярный угол лежит в третьей четверти: , то

. (8)

п.3. Геометрическая интерпретация комплексных чисел. Комплексная плоскость.

Пусть на плоскости введена ПДСК, тогда каждую точку плоскости можно отождествить с упорядоченной парой действительных чисел, которые являются ее координатами: или просто .

С другой стороны, каждое комплексное число можно также отождествить с упорядоченной парой действительных чисел , где – действительная часть комплексного числа z, – мнимая часть комплексного числа z.

Отсюда выводим, что каждое комплексное число можно отождествить с точкой координатной плоскости.

Определение. Координатная плоскость, каждая точка которой отождествлена с комплексным числом, называется комплексной плоскостью. Ось абсцисс Ох называется действительной осью, Ось ординат Оу называется мнимой осью.

Замечание. Существует взаимно однозначное соответствие между точками координатной плоскости и их радиус-векторами. Поэтому также существует взаимно однозначное соответствие и между всеми комплексными числами и радиус-векторами соответствующих точек комплексной плоскости.

рис.4.

Итак, чтобы изобразить комплексное число z точкой на комплексной плоскости нужно записать его в алгебраической форме записи, найти его действительную и мнимую части и построить в ПДСК на этой плоскости точку, абсцисса которой равна действительной части, а ордината – мнимой части данного комплексного числа z:

,

где вектор является радиус-вектором точки z.

Введем на комплексной плоскости полярную систему координат стандартным образом совмещенную с ПДСК, т.е. с полюсом в начале координат и полярным лучом, совмещенным с положительной полуосью абсцисс. Тогда точка z имеет полярные координаты , где r – полярный радиус точки z, а – ее полярный угол.

Замечание. В дальнейшем мы постоянно и молчаливо будем подразумевать, что на комплексной плоскости введена полярная система координат стандартным образом совмещенная с ПДСК и, что любое комплексное число отождествлено с точкой комплексной плоскости и имеет на этой плоскости как декартовые координаты, так и полярные.

При такой геометрической интерпретации комплексного числа как точки на комплексной плоскости ее полярные координаты, как и декартовые, получили специальные названия и обозначения.

Определение. Модулем комплексного числа называется полярный радиус точки комплексной плоскости отождествленной с этим числом.

Определение. Аргументом комплексного числа называется полярный угол точки комплексной плоскости отождествленной с этим числом.

Обозначения: – модуль комплексного числа z,

– аргумент комплексного числа z.

Таким образом, полярными координатами точки z комплексной плоскости являются модуль и аргумент комплексного числа z:

.

Из определений следует, что , или .

Можно дать такое определение модуля комплексного числа совпадающее с первым.

Определение. Модулем комплексного числа называется расстояние от начала координат комплексной плоскости до точки, отождествленной с этим числом.

Замечание. Так как действительные числа изображаются здесь точками на координатной оси Ох, то данное выше определение модуля комплексного числа является одновременно и определением модуля действительного числа.

Определение. Модулем действительного числа называется расстояние от начала координат до точки числовой оси, отождествленной с этим числом.

(Замечу в скобках, что я бесконечно благодарен своей ученице Алене Гузнищевой, от которой я и услышал эту чеканную формулировку определения модуля действительного числа. А училась она тогда в 8-м классе.)

п.4. Тригонометрическая форма записи комплексного числа.

Если точка z комплексной плоскости имеет декартовые координаты (х, у), т.е. и полярные , то они связаны соотношением (1):

.

По определению, и из (1) получаем:

. (9)

Подставляя в алгебраическую форму записи числа z получаем: . Или

(10)

Определение. Запись комплексного числа в виде (3) называется его тригонометрической формой.

Замечание. Поскольку одну букву писать экономнее нежели несколько, то чаще всего тригонометрическую форму комплексного числа пишут в виде:

, (11)

где .

Теорема. (О равенстве комплексных чисел в тригонометрической форме.)

Два комплексных числа равны тогда и только тогда, когда равны их модули и аргументы.

Доказательство. Так как между всеми комплексными числами и всеми точками комплексной плоскости существует взаимно однозначное соответствие, то равные комплексные числа отождествляются на комплексной плоскости с одной и той же точкой, следовательно, имеют одни и те же полярные координаты, т.е. полярный радиус, который по определению равен модулю комплексного числа, и полярный угол, который по определению равен аргументу комплексного числа. Обратно, если комплексные числа имеют равные модули и аргументы, то они изображаются на комплексной плоскости одной точкой и, следовательно, равны.

Теорема доказана.

Используя соотношения, которые связывают полярные и декартовые координаты точки плоскости, можно найти модуль и аргумент комплексного числа зная его действительную и мнимую части.

Пусть , т.е. , . Тогда

, (12)

, если точка z лежит в первой или четвертой четверти или , если точка z лежит во второй или третьей четверти. Также можно пользоваться формулами (6) – (8) п.1, где .

Пример. Найти тригонометрическую форму записи комплексного числа z, если:

а) ; б) ; в) ; г) ; д) .

Решение. а) , .

, .

Ответ: .

б) , , , .

Ответ: .

в) , , , .

Ответ: .

г) , , , .

Ответ: .

д) , , ,

.

Ответ: , где .

Замечание. В некоторых случаях удобнее не пользоваться формулами, а изображать на чертеже соответствующую точку на комплексной плоскости и находить модуль и аргумент комплексного числа пользуясь чертежом. Например, найдем тригонометрическую форму комплексного числа .

Число соответствует на комплексной плоскости точке . Отметим ее на координатной плоскости:

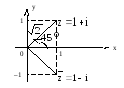
рис.5.

Из рис.5 мы сразу же видим, что и . Отсюда, .

Найдем, далее тригонометрическую форму числа комплексно сопряженного числу , т.е. .

Из рис.5 мы видим, что , и

или .

Замечание. Несмотря на то, что , а , форма записи комплексного числа z с аргументом в виде не является тригонометрической, т.к. . В этом случае правильной записью тригонометрической формы комплексного числа будет:

или .

п.5. Умножение комплексных чисел в тригонометрической форме записи. Свойства модуля комплексных чисел.

Теорема. (Об умножении комплексных чисел в тригонометрической форме записи.)

Пусть , где и , где – два произвольных комплексных числа записанных в тригонометрической форме. Тогда

. (13)

Доказательство.

, ч.т.д.

Теорема доказана.

Отсюда вытекает правило умножения комплексных чисел в тригонометрической форме записи.

Для того, чтобы перемножить два комплексных числа в тригонометрической форме записи нужно перемножить их модули, а аргументы сложить.

Следствие 1. Пусть k натуральное число и . Пусть далее , где – произвольные n комплексных чисел записанных в тригонометрической форме записи. Тогда

.

Доказательство проводится индукцией по числу сомножителей и предоставляется читателю.

Следствие 2. Пусть n натуральное число и – произвольное комплексное число в тригонометрической форме записи. Тогда

.

Доказательство сразу же следует из Следствия 1.

Теорема. (Свойства модуля комплексного числа.)

Пусть – произвольные комплексные числа и соответствующие точки на комплексной плоскости. Тогда:

1) и . Т.е. модуль произведения комплексных чисел равен произведению их модулей и модули противоположных чисел равны;

2) расстояние между точками и комплексной плоскости равно модулю разности соответствующих комплексных чисел: ;

3) ;

4) ;

Доказательство. 1) По предыдущей теореме имеем:

, где и ,

т.е. .

Таким образом, равенства и есть тригонометрическая форма записи числа , следовательно, по теореме о равенстве комплексных чисел в тригонометрической форме записи, имеем , ч.т.д.

Далее, т.к. , то по только что доказанному свойству , ч.т.д.

Заметим, что последнее равенство можно получить и из других соображений.

Противоположные числа на комплексной плоскости изображаются точками симметричными относительно начала координат. Действительно, пусть . Тогда и точки , имеют противоположные декартовые координаты. Значит, в силу симметрии, расстояния от этих точек до начала координат равны, т.е. , ч.т.д. Заметим, также, что такой же результат можно получить с помощью формулы (12) вычисления модуля комплексного числа.

2). Пусть , . Тогда и по формуле (12) имеем:

. (14)

С другой стороны, рассмотрим числа и как точки на комплексной плоскости. Тогда точка имеет декартовые координаты , а и искомое расстояние между ними вычисляется по формуле (14), ч.т.д.

3) Рассмотрим на комплексной плоскости точки , и начало координат О. В общем случае эти три точки являются вершинами треугольника :

рис.6.

Воспользуемся известным свойством треугольника: длина стороны треугольника не превосходит суммы длин двух его других сторон.

Мы только что доказали, что длина стороны этого треугольника равна , а длины сторон и равны по определению модулям чисел и : , . Отсюда и получаем, что .

Заменим в последнем неравенстве число на противоположное число , тогда получаем:

, ч.т.д.

Заметим, что равенство в этих неравенствах достигается тогда и только тогда, когда треугольник вырождается в отрезок прямой, т.е. когда все три точки О, и лежат на одной прямой.

4) , откуда следует

. Поменяв местами и , получаем

, откуда и следует доказываемое неравенство.

Теорема доказана.

Теория комплексных чисел имеет много приложений в различных областях математики. Не могу удержаться от искушения привести хотя бы один такой пример, относящийся к области теории чисел.