- •Вопрос 1. Понятие систем линейных уравнений. Их решения.
- •Вопрос 2.Методы решение систем линейных уравнений.
- •Вопрос 3. Определители 2-го и 3-го порядка
- •Вопрос 4 Определители n-го порядка.
- •Вопрос 5. Понятие минора и алгебраического дополнения.
- •Вопрос 6. N-мерные векторы, операции над ними.
- •Вопрос 7 Понятие эн-мерного векторного пространства. Линейная зависимость вектора.
- •Вопрос 10. Ранг матрицы.
- •Вопрос 8. Определение ранга матрицы
- •Вопрос 9.10.11
- •Вопрос 12.Обратная матрица
- •Вопрос 15. Плоскость. Взаимное расположение плоскостей.
- •Вопрос 16. Взаимное расположение прямой и плоскости в пространстве.
- •Вопрос 17. Основные понятия и свойства функций
- •Вопрос 18.Понятие элементарной функции и их классификация.
- •Вопрос 19.Числовая последовательность и её пределы.
- •Вопрос 20. Предел функции основные понятия о пределах. Понятие бесконечно малых и бесконечно больших величин
- •Вопрос 24. Правила дифференцирования
- •25. Производная основный элементарных функций. Таблица производных
- •Вопрос 26. Понятие Дифференциала и его свойства. (продолжение вопрос 24)
- •Вопрос 27. Теорема о промежуточном значении.
- •Вопрос28.Применение производной в исследовании функций
- •Вопрос 29:Понятие экстремума функции
- •Вопрос 30. Выпуклые функции.
- •Вопрос 33.
- •Вопрос 34. Экстремумы функций нескольких переменных. (Не весь)
- •Вопрос 36 Методы интегрирования.
- •Вопрос 37. Определенный интеграл Римана, Дарбу, Ньютона-Лейбница, виды интегрируемых функций.
- •Вопрос 39 Несобственные интегралы
Вопрос 12.Обратная матрица
Обра́тная ма́трица — такая матрицаA−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицуE:
![]()
Квадратная матрицаобратима тогда и только тогда, когда она невырожденная, то есть еёопределительне равен нулю. Для неквадратных матриц ивырожденных матрицобратных матриц не существует. Однако возможно обобщить это понятие и ввестипсевдообратные матрицы, похожие на обратные по многим свойствам.
Свойства обратной матрицы
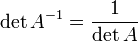 ,
где
,
где 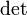 обозначаетопределитель.
обозначаетопределитель.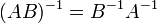 для
любых двух обратимых матриц
для
любых двух обратимых матриц 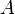 и
и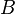 .
.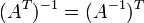 где
где 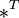 обозначает
транспонированную матрицу.
обозначает
транспонированную матрицу.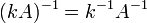 для
любого коэффициента
для
любого коэффициента 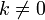 .
.Если необходимо решить систему линейных уравнений
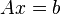 ,
(b — ненулевой вектор) где
,
(b — ненулевой вектор) где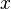 —
искомый вектор, и если
—
искомый вектор, и если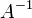 существует,
то
существует,
то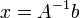 .
В противном случае либо
размерностьпространстварешений
больше нуля, либо их нет вовсе.
.
В противном случае либо
размерностьпространстварешений
больше нуля, либо их нет вовсе.
Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться одним из следующих способов:
Метод Гаусса—Жордана
Возьмём две матрицы: саму A и единичнуюE. Приведём матрицу A к единичной матрице методом Гаусса—Жордана. После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равнойA−1.
При
использовании метода Гаусса первая
матрица будет умножаться слева на одну
из элементарных матриц ![]() (трансвекциюилидиагональную
матрицус единицами на главной
диагонали, кроме одной позиции):
(трансвекциюилидиагональную
матрицус единицами на главной
диагонали, кроме одной позиции):
![]() .
.
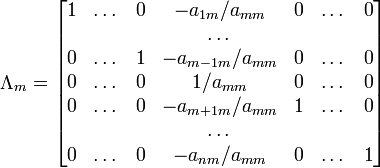 .
.
Вторая
матрица после применения всех операций
станет равна ![]() ,
то есть будет искомой. Сложность
алгоритма —
,
то есть будет искомой. Сложность
алгоритма —![]() .
.
С помощью матрицы алгебраических дополнений
![]()
![]() —транспонированная матрица
алгебраических дополнений;
—транспонированная матрица
алгебраических дополнений;
Полученная матрица A−1 и будет обратной. Сложность алгоритма зависит от сложности алгоритма расчета определителя Odet и равна O(n²)·Odet.
Иначе говоря, обратная матрица равна единице, делённой на определительисходной матрицы и умноженной натранспонированную матрицуалгебраических дополненийэлементов исходной матрицы.
Выбор начального приближения
Проблема
выбора начального приближения ![]() в
рассматриваемых здесь процессах
итерационного обращения матриц не
позволяет относиться к ним как к
самостоятельным универсальным методам,
конкурирующими с прямыми методами
обращения, основанными, например, на
LU-разложении матриц. Имеются некоторые
рекомендации по выбору
в
рассматриваемых здесь процессах
итерационного обращения матриц не
позволяет относиться к ним как к
самостоятельным универсальным методам,
конкурирующими с прямыми методами
обращения, основанными, например, на
LU-разложении матриц. Имеются некоторые
рекомендации по выбору![]() ,
обеспечивающие выполнение
условия
,
обеспечивающие выполнение
условия![]() (спектральный
радиус матрицы меньше единицы), являющегося
необходимым и достаточным для сходимости
процесса. Однако при этом, во-первых,
требуется знать сверху оценку спектра
обращаемой матрицы A либо матрицы
(спектральный
радиус матрицы меньше единицы), являющегося
необходимым и достаточным для сходимости
процесса. Однако при этом, во-первых,
требуется знать сверху оценку спектра
обращаемой матрицы A либо матрицы![]() (а
именно, если A — симметричная
положительно определённая матрица и
(а
именно, если A — симметричная
положительно определённая матрица и![]() ,
то можно взять
,
то можно взять![]() ,
где
,
где![]() ;
если же A — произвольная невырожденная
матрица и
;
если же A — произвольная невырожденная
матрица и![]() ,
то полагают
,
то полагают![]() ,
где также
,
где также![]() ;
можно конечно упростить ситуацию и,
воспользовавшись тем, что
;
можно конечно упростить ситуацию и,
воспользовавшись тем, что![]() ,
положить
,
положить![]() ).
Во-вторых, при таком задании начальной
матрицы нет гарантии, что
).
Во-вторых, при таком задании начальной
матрицы нет гарантии, что![]() будет
малой (возможно, даже окажется
будет
малой (возможно, даже окажется![]() ),
и высокий порядок скорости сходимости
обнаружится далеко не сразу.
),
и высокий порядок скорости сходимости
обнаружится далеко не сразу.
Примеры
Матрица 2х2
![]()
Обращение
матрицы 2х2 возможно только при условии,
что ![]() .
.
вопрос 13Кривые второго порядка. К кривым второго порядка относятся эллипс, гипербола и парабола. Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих декартовых координат. В общем случае Ах2 + 2Вху +Су2 + 2Дх + 2Еу +F = 0, где А, В, С, Д, Е, F – действительные числа и по крайней мере одно из чисел А2+В2+С2≠0.
Эллипс.Эллипсом называется геометрическое место точек в плоскости, сумма расстояний каждой из которых от двух данных точек этой плоскости называется фокусами (постоянная величина).
Каноническое уравнение эллипса:
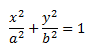
Х и у принадлежат эллипсу. а – большая полуось эллипса. b – малая полуось эллипса
У эллипса 2 оси симметрии ОХ и ОУ. Оси симметрии эллипса – его оси, точка их пересечения – центр эллипса. Та ось на которой расположены фокусы, называется фокальной осью. Точка пересечения эллипса с осями – вершина эллипса. Коэффициент сжатия (растяжения): ε = с/а – эксцентриситет (характеризует форму эллипса), чем он меньше, тем меньше вытянут эллипс вдоль фокальной оси.
Если центры эллипса находятся не в центре С(α, β)
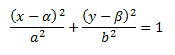
Гипербола. Гиперболой называется геометрическое место точек в плоскости, абсолютная величина разности расстояний, каждое из которых от двух данных точек этой плоскости, называемых фокусами есть величина постоянная , отличная от ноля.
Каноническое уравнение гиперболы
![]()
Гипербола имеет 2 оси симметрии: а – действительная полуось симметрии ,b – мнимая полуось симметрии
Ассимптоты гиперболы:
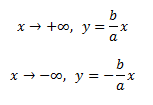
Парабола. Параболой называется геометрическое место точек в плоскости, равноудаленных от данной точки F, называемой фокусом и данной прямой, называемой директрисой.
Каноническое уравнение параболы: У2=2рх, где р – расстояние от фокуса до директрисы (параметр параболы)
Если
вершина параболы С (α, β), то уравнение
параболы (у-β)2=2р(х-α)
Вопрос
14.Прямая в пространстве. Взаимное
расположение прямых.

Взаимное расположение прямых.
Возможны четыре различных случая расположения двух прямых в пространстве:
– прямые скрещивающиеся, т.е. не лежат в одной плоскости;
– прямые пересекаются, т.е. лежат в одной плоскости и имеют одну общую точку;
– прямые параллельные, т.е. лежат в одной плоскости и не пересекаются;
– прямые совпадают.
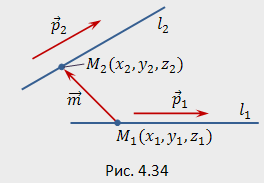
Получим признаки этих случаев взаимного расположения прямых, заданных каноническими уравнениями:
где ![]() —
точки, принадлежащие прямым
—
точки, принадлежащие прямым ![]() и
и ![]() соответственно,
a
соответственно,
a ![]()
![]() —
направляющие векторы (рис.4.34). Обозначим
через вектор,
соединяющий заданные точки.
—
направляющие векторы (рис.4.34). Обозначим
через вектор,
соединяющий заданные точки.
Расстояние между параллельными прямыми.
Найдем
расстояние ![]() между
параллельными прямыми, заданными
каноническими уравнениями (рис.4.35)
между
параллельными прямыми, заданными
каноническими уравнениями (рис.4.35)
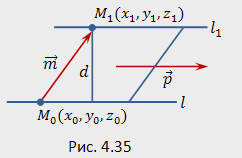
где ![]() —
произвольные точки на прямых
—
произвольные точки на прямых ![]() и
и ![]() соответственно,
а координаты направляющих векторов
прямых пропорциональны:
соответственно,
а координаты направляющих векторов
прямых пропорциональны: ![]()
Искомое
расстояние ![]() равно
высоте параллелограмма, построенного
на векторах
равно
высоте параллелограмма, построенного
на векторах![]() и ,
и может быть найдено по формуле (4.35).
и ,
и может быть найдено по формуле (4.35).
Напомним, что расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра, т.е. кратчайшее расстояние между точками этих прямых.