Вопрос 20. Предел функции основные понятия о пределах. Понятие бесконечно малых и бесконечно больших величин

Определение. Число А называется пределом функции f(x) при х→а, если для любого ε>0 существует такое число Δ>0, что для всех х таких, что

0 < ⎪x - a⎪ < Δ

верно неравенство ⎪f(x) - A⎪< ε.

Определение. Если f(x) → A1 при х → а только при x < a, то limf(x)=A1- называется пределом функции f(x) в точке х = а слева, а если f(x) → A2 при х → а только при x > a, то называется пределом функции f(x) в точке х = а справа.

Приведенное выше определение относится к случаю, когда функция f(x) не определена в самой точке х = а, но определена в некоторой сколь угодно малой окрестности этой точки.

Пределы А1 и А2 называются также односторонними пределами функции f(x) в точке х = а. Также говорят, что А – конечный предел функции f(x).

Основные теоремы о пределах.

Теорема 1. , Предел постоянной величины равен самой постоянной величине.(limC=C)

Следующие теоремы справедливы при предположении, что функции f(x) и g(x) имеют конечные пределы при х→а.

Теорема 2. Lim(F(x)+-g(x)) = limf(x)+-limg(x)

Представим f(x) = A + α(x), g(x) = B + β(x), где lim f(x) =A, lim g(x) =B тогда

f(x) ± g(x) = (A + B) + α(x) + β(x)

A + B = const, α(х) + β(х) – бесконечно малая, значит lim(f(x)+- g(x)) = A+B = limf(x) +- limg(x).

Теорема 3.

Lim(f(x) * g(x) ) = Lim f(x) * lim g(x)

Следствие

Lim C * f(x) = C * lim f(x)

Доказательство

Представим f(x) = A + α(x), g(x) = B + β(x), где lim f(x) =A, lim g(x) =B тогда f(x) * g(x) = (A * B) +Aβ(x)* α(x)B+ α(x)β(x)

A⋅B = const, α(х) и β(х) – бесконечно малые, значит lim(f(x)*g(x)) =lim A*B + 0= A*B=limf(x) * lim g(x)

Теорема 4.

Limf(x) \g(x) = lim f(x)\ lim g(x)

Теорема 5.

Если f(x)>0 вблизи точки х = а и lim f(x) =A, то А>0.

Аналогично определяется знак предела при f(x) < 0, f(x) ≥ 0, f(x) ≤ 0.

Теорема 6. Если g(x) ≤ f(x) ≤ u(x) вблизи точки х = а иlimg(x) = lim u(x)= A, то и Lim=A

Определение. Функция f(x) называется ограниченной вблизи точки х = а, если существует такое число М>0, что ⎪f(x)⎪<M вблизи точки х = а.

Теорема 7. Если функция f(x) имеет конечный предел при х→а, то она ограничена вблизи точки х = а.

Бесконечно малые функции.

Определение. Функция y=f(x) называется бесконечно малой при x→a или при x→∞, если lim f(x) =0 , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.

Бесконечно малой функция может быть только если указать к какому числу стремится аргумент х. При различных значениях а функция может быть бесконечно малой или нет.

Теорема. Для того, чтобы функция f(x) при х→а имела предел, равный А, необходимо и достаточно, чтобы вблизи точки х = а выполнялось условие

f(x) = A + α(x),

где α(х) – бесконечно малая при х → а (α(х)→0 при х → а).

Свойства бесконечно малых функций:

1.Сумма фиксированного числа бесконечно малых функций при х→а тоже бесконечно малая функция при х→а.

Доказательство

Итак, зафиксируем произвольное число ε>0. Так как по условию теоремы α(x) – бесконечно малая функция, то найдется такое δ1>0, что при |x – a|<δ1 имеем |α(x)|< ε/2. Аналогично, так как β(x) – бесконечно малая, то найдется такое δ2>0, что при |x – a|<δ2 имеем | β(x)|< ε/2.

Возьмем δ=min{ δ1, δ2}.Тогда в окрестности точки a радиуса δбудет выполняться каждое из неравенств |α(x)|< ε/2 и | β(x)|< ε/2. Следовательно, в этой окрестности будет

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)| < ε/2 + ε/2= ε,

т.е. |f(x)|<ε, что и требовалось доказать.

2.Произведение фиксированного числа бесконечно малых функций при х→а тоже бесконечно малая функция при х→а.

Доказательство. Так как функция f(x) ограничена, то существует число М такое, что при всех значениях x из некоторой окрестности точки a|f(x)|≤M. Кроме того, так как a(x) – бесконечно малая функция при x→a, то для произвольного ε>0 найдется окрестность точки a, в которой будет выполняться неравенство |α(x)|< ε/M. Тогда в меньшей из этих окрестностей имеем | αf|< ε/M= ε. А это и значит, что af – бесконечно малая. Для случая x→∞ доказательство проводится аналогично.

3.Произведение бесконечно малой функции на функцию, ограниченную вблизи точки х = а является бесконечно малой функцией при х→а.

4.Частное от деления бесконечно малой функции на функцию, предел которой не равен нулю есть величина бесконечно малая.

Бесконечно большие функции

Переменная x называется бесконечно большой, если для всякого положительного числа c существует такое значение , что каждое следующее за ним x будет по абсолютной величине больше . Пишут:

Определение. Предел функции f(x) при х→а, где а- число, равен бесконечности, если для любого числа М>0 существует такое число Δ>0, что неравенство

⎪f(x)⎪>M

выполняется при всех х, удовлетворяющих условию

0 < ⎪x - a⎪ < Δ, записывается limf(x) = бесконечности

Определение. Функция называется бесконечно большой при х→а, где а – чосли или одна из величин ∞, +∞ или -∞, если lim f (x) =A, где А – число или одна из величин ∞, +∞ или -∞

вопрос 21. Понятие непрерывности функции. Точки разрыва их классификация. Пусть задана функция y=f(x), будем называть функцию непрерывной если она удовлетворяет следующим условиям

1. Функция определена в точке х нулевое

2. Имеет конечный предел при х стремиться к х нулевому

3. Этот предел = значению функции в точке х нулевое.

1.Существуют односторонние пределы, в таком случае речь будет идти о непрерывности справа или слева. LImf(x) = f(x0)

X стремится к х0-0, функция непрерывна слева

Х стремится к х0+0, функция непрерывна с права.

Непрерывность функции в данной точке определяется непрерывностью её графика при прохождении данной точки.

2. задана у=f(x). Выберем произвольную точку х0 из области определения функции и зададим преращение дельта х, тогда соответственное преращение получит и функция, которое равно дельта у=f(x0 +дельтаx) – f(x0).

Функция у =f(x) называется непрерывной в точке х нулевое, если она определена в этой точке и бесконечно малому преращению аргумента соответственно бесконечно малое преращение функции.

Точка разрыва. Точка х нулевое называется точкой разрыва F(x), если функция в этой точке не является непрерывной. Классификация.

1. Точки разрыва первого рода

Если при х, стремящемуся к х нулевому функция имеет односторонние пределы и они не равны друг другу.

2. Точки второго рода.

если при х стремящемуся к ч нулевому хотя бы один из односторонних пределов равен бесконечности или не существует.

Замечание. К точкам первого рода можно отнести так называемые точки устранимого разрыва. Точка х нулевое называется точкой устранимого разрыва если lim функции при ч стремящемся к х нулевому существует, но он не равен значению функции в этой точке.

Свойства

1.Пусть заданы f(x) и g(x) непрерывные в точке х нулевое , тогда функция f(x)+- g(x) , f(x)* g(x), f(x)\ g(x), g(x) не равно 0, есть функции непрерывные

2. Если f(x) непрерывна в точке х нулевоеи значение функции в точке х нулевое положительно, то существует такая окрестность в точке х нулевое, в которой вся функция положительна.

3. Если функция y=F(u) непрерывна и в точке u нулевое Uнулевое = ϕ(xНулевое) , а функция U = ϕ(x) непрерывна в точке ч нулевое, то сложная функция Y=F(ϕ(x)) непрерывна в точке х нулевое.

Если функция y=f(x)непрерывна в каждой точке промежутка ав, то она непрерывна на этом промежутке.

Вопрос 22.Свойства функций непрерывной на промежутке. Пусть y=f(x) задана на промежутке ав.

Свойство 1: (Первая теорема Вейерштрасса (Вейерштрасс Карл (1815-1897)- немецкий математик)). Функция, непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке [a, b] выполняется условие –M ≤ f(x) ≤ M.

Доказательство этого свойства основано на том, что функция, непрерывная в точке х0, ограничена в некоторой ее окрестности, а если разбивать отрезок [a, b] на бесконечное количество отрезков, которые “стягиваются” к точке х0, то образуется некоторая окрестность точки х0.

Свойство 2: Функция, непрерывная на отрезке [a, b], принимает на нем наибольшее и наименьшее значения.

Т.е. существуют такие значения х1 и х2, что f(x1) = m, f(x2) = M, причем

m ≤ f(x) ≤ M

Отметим эти наибольшие и наименьшие значения функция может принимать на отрезке и несколько раз (например – f(x) = sinx).

Разность между наибольшим и наименьшим значением функции на отрезке называется колебанием функции на отрезке.

Свойство 3: (Вторая теорема Больцано – Коши). Функция, непрерывная на отрезке [a, b], принимает на этом отрезке все значения между двумя произвольными величинами.

Свойство 4: Если функция f(x) непрерывна в точке х = х0, то существует некоторая окрестность точки х0, в которой функция сохраняет знак.

Свойство 5: (Первая теорема Больцано (1781-1848) – Коши). Если функция f(x)- непрерывная на отрезке [a, b] и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где f(x) = 0.

Т.е. если sign(f(a)) ≠ sign(f(b)), то ∃ х0: f(x0) = 0.

Свойство 7: Если функция f(x) определена, монотонна и непрерывна на некотором промежутке, то и обратная ей функция х = g(y) тоже однозначна, монотонна и непрерывна.

Свойства функций, непрерывных в точке

Поскольку точки непрерывности функциизадаются условием, то часть свойств функций, непрерывных в точке, следует непосредственно из свойств пределов. Сформулируем их в виде следующей теоремы.

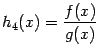Теорема 3.1   Пусть функции инепрерывны в точке. Тогда функции,,непрерывны в точке. Если, то функциятакже непрерывна в точке.

        Доказательство.     Оно сразу же следует из теорем о пределах 2.8, 2.9, 2.10 и следствия 2.5.      

Как непосредственное следствие этой теоремы получается следующее

Предложение 3.3   Рассмотрим множество всех функций, определённых в некоторой фиксированной окрестности точкии непрерывных в этой точке. Тогда это множествоявляется линейным пространством, то есть замкнуто относительно сложения и умножения на постоянные:

        Доказательство.     Действительно, постоянные и-- это непpеpывные функции (в любой точке); по пpедыдущей теоpеме тогда непpеpывны в точкепpоизведенияи. Но тогда по этой же теоpеме непpеpывна в точкеи сумма.

        Теорема 3.2   Пусть функции итаковы, что существует композиция,. Пусть функциянепрерывна в точке, а функциянепрерывна в соответствующей точке. Тогда композициянепрерывна в точке.

        Доказательство.     Заметим, что равенство означает, что прибудет. Значит,

(последнее равенство следует из непрерывности функции в точке). Значит,

а это равенство означает, что композиция непрерывна в точке.

Заметим, что, очевидно, в предыдущих двух теоремах можно было бы заменить базу на односторонние базыилии получить аналогичные утверждения для непрерывности слева или справа:

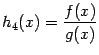        Теорема 3.3   Пусть функции инепрерывны слева (справа) в точке. Тогда функции,,непрерывны слева (соотв. справа) в точке. Если, то функциятакже непрерывна слева (спpава) в точке.

        Теорема 3.4   Пусть функция непрерывна слева (справа) в точке, а функциянепрерывна в точке. Тогда композициянепрерывна слева (соотв. справа) в точке.

Вопрос 23. Понятие производной. Пусть задана функция y=f(x), которая определена на некотором промежутке Х, х принадлежит Х и зададим достаточно малое преращение ∆х, причём таким образом, чтобы значение х+∆х не выходило за пределы промежутка, тогда соответствующее преращение получит и значение функции ∆y=f(x+∆x) – f(x).

Производной функцией y=f(x) в точке х называется предел преращения функции в этой точке к преращению аргумента при дельта х стремящемуся к нулю (если такой предел существует)

Если функция имеет производную в каждой точке промежутка Х, то её называют дифференцируемой на промежутке Х.

Производная f’(x) есть угловой коэффициент касательной проведённой к графику функции в точке х нулевое (tg угла наклона)

Так как существует односторонний предел, то можно говорить об односторонних производных

Lim= ∆x\∆y= f’(x) (f с минусом внизу) – слева ; F с плюсом внизу справа.

Теорема. Если функция дифференцируема в точке х нулевое, то она в этой точке непрерывна. Обратная теорема не верна. Таким образом непрерывность функции есть необходимое , но недостаточное условие её дифференцируемости.

Физический смысл производной функции

Если положение точки при её движении по числовой прямой задаётся функцией S = f(t), где t – время движения, то производная функции S – мгновенная скорость движения в момент времени t. По аналогии с этой моделью вообще говорят о том, что производная функции у = f(x) – скорость изменения функции в точке х.