
- •Вопрос 1. Понятие систем линейных уравнений. Их решения.
- •Вопрос 2.Методы решение систем линейных уравнений.
- •Вопрос 3. Определители 2-го и 3-го порядка
- •Вопрос 4 Определители n-го порядка.
- •Вопрос 5. Понятие минора и алгебраического дополнения.
- •Вопрос 6. N-мерные векторы, операции над ними.
- •Вопрос 7 Понятие эн-мерного векторного пространства. Линейная зависимость вектора.
- •Вопрос 10. Ранг матрицы.
- •Вопрос 8. Определение ранга матрицы
- •Вопрос 9.10.11
- •Вопрос 12.Обратная матрица
- •Вопрос 15. Плоскость. Взаимное расположение плоскостей.
- •Вопрос 16. Взаимное расположение прямой и плоскости в пространстве.
- •Вопрос 17. Основные понятия и свойства функций
- •Вопрос 18.Понятие элементарной функции и их классификация.
- •Вопрос 19.Числовая последовательность и её пределы.
- •Вопрос 20. Предел функции основные понятия о пределах. Понятие бесконечно малых и бесконечно больших величин
- •Вопрос 24. Правила дифференцирования
- •25. Производная основный элементарных функций. Таблица производных
- •Вопрос 26. Понятие Дифференциала и его свойства. (продолжение вопрос 24)
- •Вопрос 27. Теорема о промежуточном значении.
- •Вопрос28.Применение производной в исследовании функций
- •Вопрос 29:Понятие экстремума функции
- •Вопрос 30. Выпуклые функции.
- •Вопрос 33.
- •Вопрос 34. Экстремумы функций нескольких переменных. (Не весь)
- •Вопрос 36 Методы интегрирования.
- •Вопрос 37. Определенный интеграл Римана, Дарбу, Ньютона-Лейбница, виды интегрируемых функций.
- •Вопрос 39 Несобственные интегралы
Вопрос 10. Ранг матрицы.
Прямоугольная матрица с s-строками и n-столбцами А: а11…а1n
as1…asn.
Каждый столбец А можно рассмотреть как эс-мерный вектор. И отмечаем, что данная система векторов может быть линейно-зависимая или линейно-независимая.
Ранг системы столбцов – максимальное число линейно-независимых столбцов матрицы А (ранг матрицы А).
Каждую строку А можно рассматривать как эн-мерный вектор→ранг системы строк как максимальное число линейно-независимых строк.
Произвольное число k, удовлетворяющее что k≤min(s;n). Зафиксируем в матрице А произвольное k строк и k столбцов, элементы, стоящие на пересечении выбранных строк и столбцов образуют квадратную матрицу, определитель которой является минором k порядка матрицы А.
Вопрос 8. Определение ранга матрицы
Рассмотрим
прямоугольную матрицу. Если в этой
матрице выделить произвольно k строк и
k столбцов, то элементы, стоящие на
пересечении выделенных строк и столбцов,
образуют квадратную матрицу k-го порядка.
Определитель этой матрицы называется
минором k-го порядка матрицы А. Очевидно,
что матрица А обладает минорами любого
порядка от 1 до наименьшего из чисел m и
n. Среди всех отличных от нуля миноров
матрицы А найдется по крайней мере один
минор, порядок которого будет наибольшим.
Наибольший из порядков миноров данной
матрицы, отличных от нуля, называется
рангом матрицы. Если ранг матрицы А
равен r, то это означает, что в матрице
А имеется отличный от нуля минор порядка
r, но всякий минор порядка, большего чем
r, равен нулю. Ранг матрицы А обозначается
через r(A). Очевидно, что выполняется
соотношение
![]()
Вопрос 9.10.11
Операция сложения двух матриц.
Определение операции сложения двух матриц.
Операция сложения определена ТОЛЬКО ДЛЯ МАТРИЦ ОДНОГО ПОРЯДКА. Другими словами, нельзя найти сумму матриц разной размерности и вообще нельзя говорить о сложении матриц разной размерности. Также нельзя говорить о сумме матрицы и числа или о сумме матрицы и какого-нибудь другого элемента.
Определение.
Сумма
двух матриц ![]() и
и![]() -
это матрица, элементы которой равны
сумме соответствующих элементов
матрицА и В,
то есть,
-
это матрица, элементы которой равны
сумме соответствующих элементов
матрицА и В,
то есть, ![]() .
.
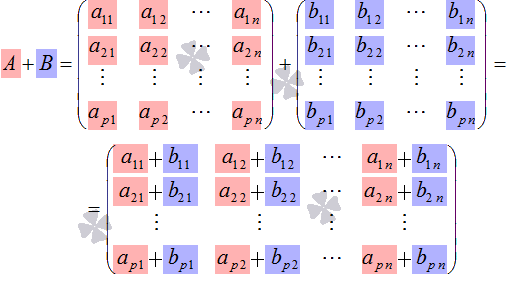
Таким образом, результатом операции сложения двух матриц является матрица того же порядка.
Свойства операции сложения матриц.
Какими же свойствами обладает операция сложения матриц? На этот вопрос достаточно легко ответить, отталкиваясь от определения суммы двух матриц данного порядка и вспомнив свойства операции сложения действительных (или комплексных) чисел.
Для матриц А, В и С одного порядка характерно свойство ассоциативности сложения А+(В+С)=(А+В)+С.
Для матриц данного порядка существует нейтральный элемент по сложению, которым является нулевая матрица. То есть, справедливо свойство А+О=А.
Для ненулевой матрицы А данного порядка существует матрица (–А), их суммой является нулевая матрица: А+(-А)=О.
Для матриц А и В данного порядка справедливо свойство коммутативности сложения А+В=В+А.
Следовательно, множество матриц данного порядка порождает аддитивную группу Абеля (абелеву группу относительно алгебраической операции сложения).
Сложение матриц - решения примеров.
Рассмотрим несколько примеров сложения матриц.
Пример.
Найдите
сумму матриц 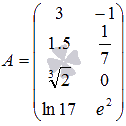 и
и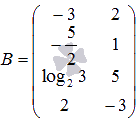 .
.
Решение.
Порядки
матриц А и В совпадают
и равны 4 на 2,
поэтому мы можем проводить операцию
сложения матриц и в результате должны
получить матрицу порядка 4 на 2.
Согласно определению операции сложения
двух матриц, сложение производим
поэлементно:
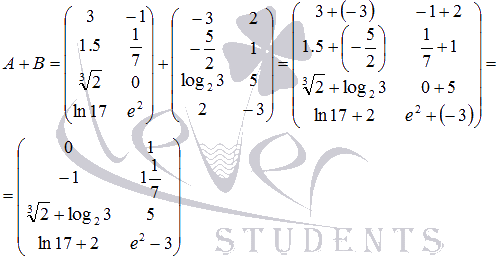
Пример.
Найдите
сумму двух матриц ![]() и
и![]() элементами
которых являются комплексные числа.
элементами
которых являются комплексные числа.
Решение.
Так
как порядки матриц равны, то мы можем
выполнить сложение.
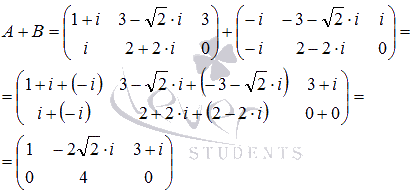
Пример.
Выполните
сложение трех матриц 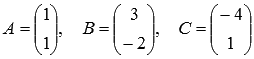 .
.
Решение.
Сначала
сложим матрицу А с В,
затем к полученной матрице прибавим С:
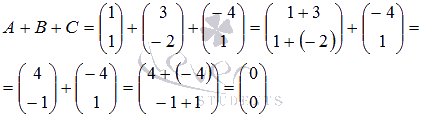
Получили нулевую матрицу.
Операция умножения матрицы на число.
Определение операции умножения матрицы на число.
Операция умножения матрицы на число определена ДЛЯ МАТРИЦ ЛЮБОГО ПОРЯДКА.
Определение.
Произведение
матрицы ![]() и
действительного (или комплексного)
числа
и
действительного (или комплексного)
числа ![]() -
это матрица, элементы которой получаются
умножением соответствующих элементов
исходной матрицы на число
-
это матрица, элементы которой получаются
умножением соответствующих элементов
исходной матрицы на число![]() ,
то есть,
,
то есть,![]() .
.
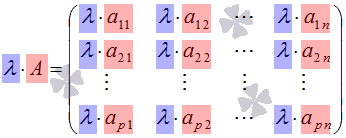
Таким образом, результатом умножения матрицы на число является матрица того же порядка.
Свойства операции умножения матрицы на число.
Для матриц одного порядка А и В, а также произвольного действительного (или комплексного) числа
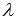 справедливо
свойство дистрибутивности умножения
относительно сложения
справедливо
свойство дистрибутивности умножения
относительно сложения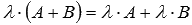 .
.Для произвольной матрицы А и любых действительных (или комплексных) чисел
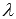 и
и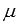 выполняется
свойство дистрибутивности
выполняется
свойство дистрибутивности .
.Для произвольной матрицы А и любых действительных (или комплексных) чисел
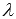 и
и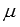 справедливо
свойство ассоциативности умножения
справедливо
свойство ассоциативности умножения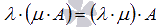 .
.Нейтральным числом по умножению на произвольную матрицу А является единица, то есть,
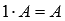 .
.
Из свойств операции умножения матрицы на число следует, что умножение нулевой матрицы на число ноль даст нулевую матрицу, а произведение произвольного числа и нулевой матрицы есть нулевая матрица.
Умножение матрицы на число - примеры и их решение.
Разберемся с проведением операция умножения матрицы на число на примерах.
Пример.
Найдите
произведение числа 2 и
матрицы 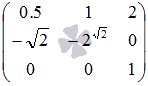 .
.
Решение.
Чтобы
умножить матрицу на число, нужно каждый
ее элемент умножить на это число:
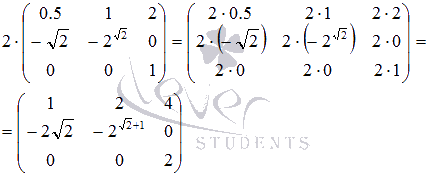
Пример.
Выполните
умножение матрицы ![]() на
число
на
число![]() .
.
Решение.
Умножаем
каждый элемент заданной матрицы на
данное число:
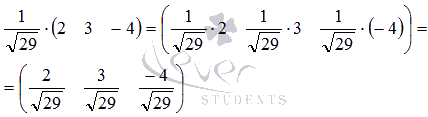
Операция умножения двух матриц.
Определение операции умножения двух матриц.
Операция умножения двух матриц А и В определяется только для случая, когда ЧИСЛО СТОЛБЦОВ МАТРИЦЫ А РАВНО ЧИСЛУ СТРОК МАТРИЦЫ В.
Определение.
Произведение
матрицы А порядка ![]() и
матрицыВ порядка
и
матрицыВ порядка ![]() -
это такая матрица С порядка
-
это такая матрица С порядка ![]() ,
каждый элемент которой равен сумме
произведений элементовi-ой строки
матрицы А на
соответствующие элементы j-ого столбца
матрицыВ,
то есть,
,
каждый элемент которой равен сумме
произведений элементовi-ой строки
матрицы А на
соответствующие элементы j-ого столбца
матрицыВ,
то есть,
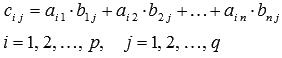
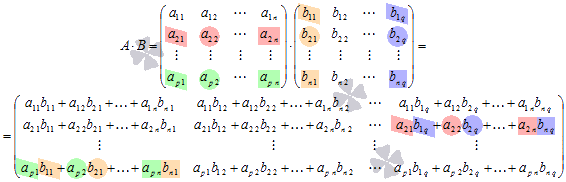
Таким
образом, результатом операции умножения
матрицы порядка ![]() на
матрицу порядка
на
матрицу порядка![]() является
матрица порядка
является
матрица порядка![]() .
.
Умножение матрицы на матрицу - решения примеров.
Разберемся с умножением матриц на примерах, после этого перейдем к перечислению свойств операции умножения матриц.
Пример.
Найдите
все элементы матрицы С,
которая получается при умножении
матриц 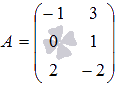 и
и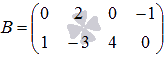 .
.
Решение.
Порядок
матрицы А равен p=3 на n=2,
порядок матрицы В равен n=2 на q=4,
следовательно, порядок порядок
произведения этих матриц будет p=3 на q=4.
Воспользуемся формулой
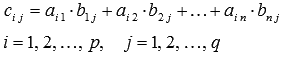
Последовательно
принимаем значения i от 1 до 3 (так
как p=3)
для каждого j от 1 до 4(так
как q=4),
а n=2 в
нашем случае, тогда
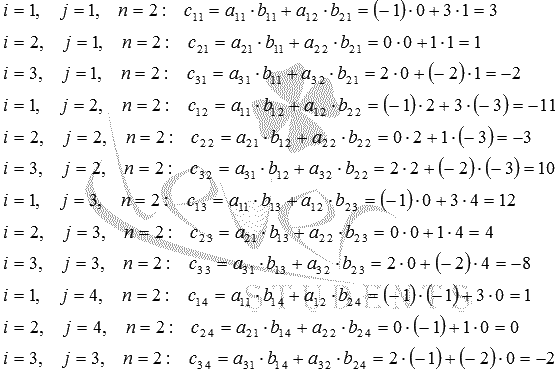
Так
вычислены все элементы матрицы С,
и матрица, полученная при умножении
двух заданных матриц, имеет вид ![]() .
.
Пример.
Выполните
умножение матриц 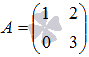 и
и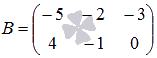 .
.
Решение.
Порядки
исходных матриц позволяют провести
операцию умножения. В результате мы
должны получить матрицу порядка 2 на
3.
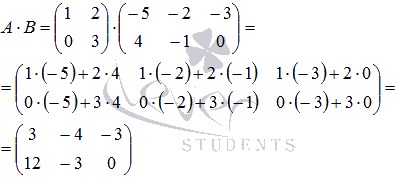
Пример.
Даны
матрицы 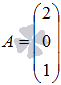 и
и![]() .
Найдите произведение матрицА и В,
а также матриц В и А.
.
Найдите произведение матрицА и В,
а также матриц В и А.
Решение.
Так
как порядок матрицы А равен 3 на 1,
а матрицы В равен 1 на 3,
то А⋅В будет
иметь порядок 3 на 3,
а произведение матриц В и A будет
иметь порядок 1 на 1.
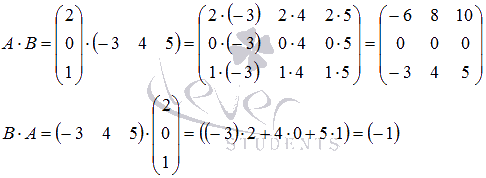
Как
видите, ![]() .
Это одно из свойств операции умножения
матриц.
.
Это одно из свойств операции умножения
матриц.
Свойства операции умножения матриц.
Если матрицы А, В и С подходящих порядков, то справедливы следующие свойства операции умножения матриц.
Свойство ассоциативности умножения матриц
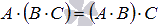 .
.Два свойства дистрибутивности
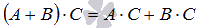 и
и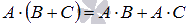 .
.В общем случае операция умножения матриц некоммутативна
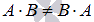 .
.Единичная матрица Е порядка n на n является нейтральным элементом по умножению, то есть, для произвольной матрицы А порядка p на n справедливо равенство
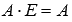 ,
а для произвольной матрицыА порядка n на p -
равенство
,
а для произвольной матрицыА порядка n на p -
равенство 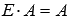 .
.
Следует отметить, что при подходящих порядках произведение нулевой матрицы О на матрицу А дает нулевую матрицу. Произведение А на О также дает нулевую матрицу, если порядки позволяют проводить операцию умножения матриц.
Среди
квадратных матриц существуют так
называемые перестановочные
матрицы,
операция умножения для них коммутативна,
то есть ![]() .
Примером перестановочных матриц является
пара единичной матрицы и любой другой
матрицы того же порядка, так как
справедливо
.
Примером перестановочных матриц является
пара единичной матрицы и любой другой
матрицы того же порядка, так как
справедливо![]() .
.
