- •Вопрос 1. Понятие систем линейных уравнений. Их решения.
- •Вопрос 2.Методы решение систем линейных уравнений.
- •Вопрос 3. Определители 2-го и 3-го порядка
- •Вопрос 4 Определители n-го порядка.
- •Вопрос 5. Понятие минора и алгебраического дополнения.
- •Вопрос 6. N-мерные векторы, операции над ними.
- •Вопрос 7 Понятие эн-мерного векторного пространства. Линейная зависимость вектора.
- •Вопрос 10. Ранг матрицы.
- •Вопрос 8. Определение ранга матрицы
- •Вопрос 9.10.11
- •Вопрос 12.Обратная матрица
- •Вопрос 15. Плоскость. Взаимное расположение плоскостей.
- •Вопрос 16. Взаимное расположение прямой и плоскости в пространстве.
- •Вопрос 17. Основные понятия и свойства функций
- •Вопрос 18.Понятие элементарной функции и их классификация.
- •Вопрос 19.Числовая последовательность и её пределы.
- •Вопрос 20. Предел функции основные понятия о пределах. Понятие бесконечно малых и бесконечно больших величин
- •Вопрос 24. Правила дифференцирования
- •25. Производная основный элементарных функций. Таблица производных
- •Вопрос 26. Понятие Дифференциала и его свойства. (продолжение вопрос 24)
- •Вопрос 27. Теорема о промежуточном значении.
- •Вопрос28.Применение производной в исследовании функций
- •Вопрос 29:Понятие экстремума функции
- •Вопрос 30. Выпуклые функции.
- •Вопрос 33.
- •Вопрос 34. Экстремумы функций нескольких переменных. (Не весь)
- •Вопрос 36 Методы интегрирования.
- •Вопрос 37. Определенный интеграл Римана, Дарбу, Ньютона-Лейбница, виды интегрируемых функций.
- •Вопрос 39 Несобственные интегралы
Вопрос 29:Понятие экстремума функции
Рассмотрим график непрерывной функции y = f(x), изображенной на рисунке №1. Значение функции в точке x1 будет больше значений функции во всех соседних точках как слева, так и справа от x1. В этом случае говорят, что функция имеет в точке x1 максимум. В другой точке x3 функция, очевидно, также имеет максимум. Если рассмотреть точку x2, то в ней значение функции меньше всех соседних значений. В этом случае говорят, что функция имеет в точке x2минимум.
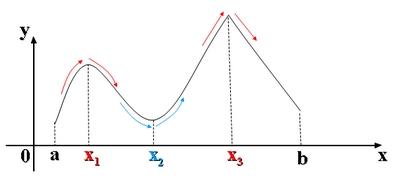
Определения
Точки, в которых функция достигает максимума или минимума, называются точками экстремума функции.
Точки максимума функции обозначаются: xmax,1, xmax,2, xmax,3 и так далее. Точки минимума функции обозначаются: xmin,1, xmin,2,xmin,3 и так далее.
Обратим внимание на то, что функция может достигать нескольких максимумов и минимумов. Отметим, что если функция имеет в точке максимум (минимум), то это не означает, что в этой точке функция имеет наибольшее (наименьшее) значение во всей области определения.
Значения функции в точках максимума или минимума функции называются экстремумами функции
Экстремумы функции обозначаются: ymin,1, ymin,2, ymin,3, ...,ymax,1, ymax,2, ymax,3 и так далее.
Функция y = f(x) в точке x0 имеет максимум, если значение функции в этой точке больше, чем ее значения во всех точках некоторого интервала, содержащего точку x0, т.е. если существует такая окрестность точки x0, что для всех x ≠ x0, принадлежащих этой окрестности, имеет место неравенство f(x) < f(x0).
Функция y = f(x) имеет минимум в точке x0, если существует такая окрестность точки x0, что для всех x ≠ x0, принадлежащих этой окрестности, имеет место неравенство f(x) > f(x0).
Алгоритм нахождения экстремумов функции
На основании теоремы о достаточных условиях экстремума функции сформулируем алгоритм нахождения экстремумов функции.
Пусть имеется непрерывная функция y = f(x), которую необходимо исследовать на предмет наличия экстремумов. Для этого следует выполнить последовательность действий:
1. Найти производную f '(x) заданной функции.
2. Найти критические точки. Для этого необходимо исследовать, в каких точках производная функции f '(x) не существует, и найти нули производной функции, т. е. решить уравнение f '(x) = 0.
3. Отметить критические точки на числовой прямой область определения функции y = f(x), после этого на числовой прямой отметить критические точки.
4. Определить знаки производной функции f '(x) на получившихся промежутках.
5. Опираясь на теорему о достаточных условиях экстремума функции, сделать выводы о наличии или отсутствии точек экстремума функции.
Вопрос 30. Выпуклые функции.
Выпуклая функция — функция, у которой надграфик является выпуклым множеством
Вещественнозначная
функция, определённая на некотором интервале(в
общем случае навыпуклом
подмножественекотороговекторного
пространства) выпукла, если для любых
двух значений аргумента![]() ,
,![]() и
для любого числа
и
для любого числа![]() выполняетсянеравенство
Йенсена:
выполняетсянеравенство
Йенсена:
![]()
Если
это неравенство является строгимдля
всех![]() и
и![]() ,
то функция называетсястрого
выпуклой;
если выполняется обратное неравенство,
функция называется вогнутой,
или выпуклой
вверх.
,
то функция называетсястрого
выпуклой;
если выполняется обратное неравенство,
функция называется вогнутой,
или выпуклой
вверх.
NB! Иногда выпуклая функция определяется как вогнутая и наоборот.
Свойства:
Функция
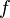 ,
выпуклая на интервале
,
выпуклая на интервале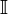 ,непрерывнана
всём
,непрерывнана
всём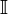 ,дифференцируемана
всём
,дифференцируемана
всём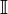 за
исключением не более чемсчётного
множестваточек и дважды
дифференцируема почти везде.
за
исключением не более чемсчётного
множестваточек и дважды
дифференцируема почти везде.Непрерывная функция
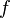 выпукла
на
выпукла
на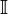 тогда
и только тогда, когда для всех
точек
тогда
и только тогда, когда для всех
точек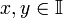 выполняется
неравенство
выполняется
неравенство
![]()
Непрерывно дифференцируемая функцияодной переменной выпукла на интервале тогда и только тогда, когда еёграфиклежит не нижекасательной, проведённой к этому графику в любой точке промежутка выпуклости.
Дважды дифференцируемая функция одной переменной выпукла на интервале тогда и только тогда, когда её вторая производнаянеотрицательна на этом интервале. Если вторая производная дважды дифференцируемой функции строго положительна, такая функция является строго выпуклой, однако обратное неверно (например, функция
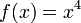 строго
выпукла на
строго
выпукла на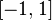 ,
но её вторая производная в точке
,
но её вторая производная в точке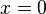 равна
нулю).
равна
нулю).Если функции
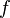 ,
,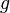 выпуклы,
то любая ихлинейная
комбинация
выпуклы,
то любая ихлинейная
комбинация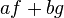 с
положительными коэффициентами
с
положительными коэффициентами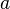 ,
,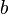 также
выпукла.
также
выпукла.Локальный минимумвыпуклой функции является такжеглобальным минимумом(соответственно, для выпуклых вверх функций локальный максимум является глобальным максимумом).
Любая стационарная точкавыпуклой функции будет глобальным экстремумом.
Для выпуклых функций выполняется неравенство Йенсена:
![]() где
где ![]() —случайная
величинасо значениями вобласти
определения функции
—случайная
величинасо значениями вобласти
определения функции![]() ,
,![]() —математическое
ожидание.
—математическое
ожидание.
Вопрос
31. Понятие функций нескольких переменных.
Пусть
![]() –
множество упорядоченных пар действительных
чисел
–
множество упорядоченных пар действительных
чисел![]() .Определение.
Если каждой упорядоченной паре чисел
.Определение.
Если каждой упорядоченной паре чисел
![]() по
некоторому закону
по
некоторому закону![]() поставлено
в соответствие единственное действительное
число
поставлено
в соответствие единственное действительное
число![]() ,
то говорят, что задана функция двух
переменных
,
то говорят, что задана функция двух
переменных![]() или
или![]() .
Числа
.
Числа![]() называются
при этом независимыми переменными или
аргументами функции, а число
называются
при этом независимыми переменными или
аргументами функции, а число![]() –
зависимой переменной.
Пару чисел
–
зависимой переменной.
Пару чисел![]() иногда
называют точкой
иногда
называют точкой![]() ,
а функцию двух переменных – функцией
точки
,
а функцию двух переменных – функцией
точки![]() .
Значение
функции
.
Значение
функции![]() в
точке
в
точке![]() обозначают
обозначают![]() или
или![]() и
называют частным значением функции
двух переменных.
Совокупность всех
точек
и
называют частным значением функции
двух переменных.
Совокупность всех
точек![]() ,
в которых определена функция
,
в которых определена функция![]() ,
называется областью определения этой
функции.
,
называется областью определения этой
функции.
Для
функции двух переменных область
определения представляет собой всю
координатную плоскость или ее часть,
ограниченную одной или несколькими
линиями.тФункция
двух независимых переменных допускает
геометрическое истолкование. Каждой
точке М0(х0;
у0)
в системе координат Oxyz соответствует
точка M(x0;y0;z0),
где z0 =
ƒ(хо;уо)
— аппликата точки М. Совокупность всех
таких точек представляет собой некоторую
поверхность, которая и будет геометрически
изображать данную функцию z=ƒ(x;у). Функция
двух переменных, как и функция одной
переменной, может быть задана разными
способами: таблицей, аналитически,
графиком. Будем пользоваться, как
правило, аналитическим способом: когда
функция задается с помощью формулы.