Вопрос 6. N-мерные векторы, операции над ними.

В разделе векторы - основные определения мы ввели понятие вектора в двумерном пространстве (на плоскости) и в трехмерном пространстве. В этой статье мы отойдем от геометрического истолкования вектора и посмотрим на него не как на направленный отрезок, а как на упорядоченный набор чисел с присущими ему свойствами. То есть, мы рассматрим векторы с позиций алгебры, что позволит расширить понятие вектора на случай n-мерного пространства. Итак, мы дадим понятие n-мерного вектора, зададим операции над n-мерными векторами, перечислим свойства этих операций и покажем их применение при решении задач.

Определение.

Упорядоченная совокупность n действительных или комплексных чисел называется n-мерным вектором.

Числа называются координатами вектора.

Векторы обозначаются строчными латинскими буквами, например, a, b, c и т.п., координаты вектора указываются в скобках.

Если записать вектор a как , то имеем вектор-строку; если записать, то имеем вектор-столбец. Это две формы записи одного и того же объекта - n-мерного вектора.

Обратите внимание: при обозначении n-мерных векторов стрелочка сверху над буквой (которая ставится при обозначении вектора на плоскости и в трехмерном пространстве) отсутствует.

Определение.

Вектор, все координаты которого равны нулю, называют нулевым вектором.

Определение.

Векторназывается противоположным вектору

Для n-мерных векторов задаются две операции: сложение векторов и умножение вектора на число.

Определение.

Суммой двух векторов иназывается вектор, координаты которого равны сумме соответствующих координат, то есть,Следует отметить, что складывать можно только векторы количество координат которых совпадает. Операция сложения для векторов, имеющих различное число координат, не определена.

Определение.

Произведением действительного или комплексного числа и вектораназывается вектор, координаты которого равны соответствующим координатам вектора а, умноженным на, то есть,

Введенные таким образом операции над n-мерными векторами при n = 2 и n = 3 полностью согласуются с операциями сложения и умножения вектора на число на плоскости и в трехмерном пространстве в геометрическом смысле. Под координатами двумерного или трехмерного вектора в этом случае понимаем координаты вектора в заданной прямоугольной системе координат на плоскости или в пространстве соответственно.

Перечислим свойства операций над n-мерными векторами.

Для любых векторов и произвольных действительных или комплексных чиселсправедливо:

1. свойство коммутативности сложения векторов a + b = b + a;

2. свойство ассоциативности векторов (a + b) + c = a + (b + c);

3. существует нейтральный вектор по операции сложения, им является нулевой вектор, a + 0 = a;

4. для любого вектора существует противоположный вектор, которые в сумме дают нулевой вектор a + (-a) = 0;

5. Сочетательное свойство умножения .

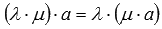6. Первое распределительное свойство .

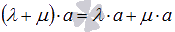7. Второе распределительное свойство .

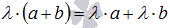8. существует нейтральное число по операции умножения, им является единица.

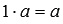Эти свойства справедливы в силу свойств операций сложения и умножения действительных или комплексных чисел.

Операции вычитания векторов как таковой нет, так как разность векторов a и b есть сумма векторов a и -b.

Перечисленные свойства операций позволяют выполнять преобразования в выражениях содержащих векторы по тем же принципам, что и в числовых выражениях.

Рассмотрим несколько примеров.

Пример.

Даны векторы 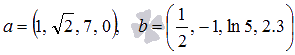. Найдите сумму и разность векторов a и b.

Решение.

Суммой двух векторов является вектор, координаты которого равны сумме соответствующих координат:

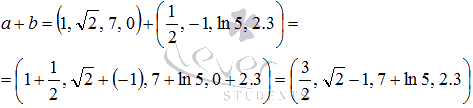
Разность векторов a и b есть сумма вектора а и вектора b, предварительного умноженного на минус единицу: 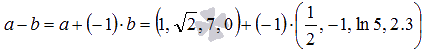. Сначала выполняется умножение вектора на число:

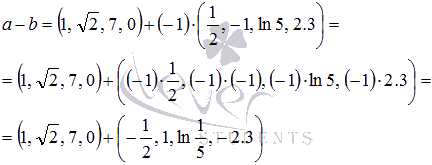
Осталось выполнить сложение:

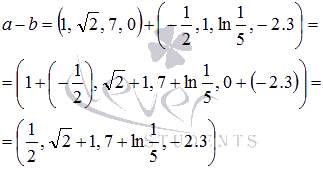
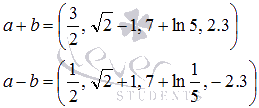
Пример.

Даны векторы . Найдите вектор .

Решение.

Сначала упростим выражение, используя свойства операций над векторами:

Теперь найдем координаты полученного вектора:

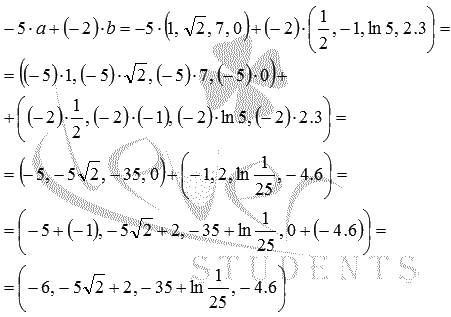
Ответ:

Пример.

Даны векторы 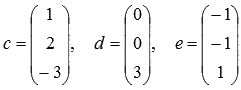. Найдите координаты вектора , выполнив необходимые операции.

Решение.

При нахождении координат вектора сначала выполним умножение вектора eна число 2, далее просуммируем соответствующие координаты:

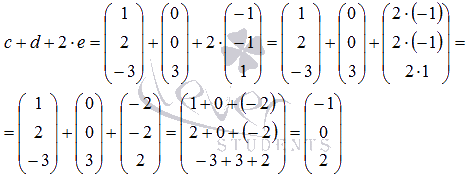
Ответ:

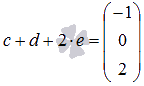
Пример.

Даны векторы . Выполните указанные действия .

Решение.

Вектор имеет четыре координаты, а вектор - три, поэтому мы не можем их сложить и, следовательно, не можем выполнить действия над векторами .

Ответ:

Мы не можем выполнить указанные действия с заданными векторами.

Множество всех n-мерных векторов с введенными операциями сложения векторов и умножения вектора на число порождают линейное пространство.

Определение.

Линейное пространство, элементами которого являются векторы, называетсявекторным или арифметическим.

Подведем итог.

Мы дали понятие n-мерного вектора, рассмотрели операции над n-мерными векторами, их свойства и увидели, что множество всех n-мерных векторов с определенными на нем операциями сложения и умножения на число порождают векторное пространство.