- •Вопрос 1. Понятие систем линейных уравнений. Их решения.
- •Вопрос 2.Методы решение систем линейных уравнений.
- •Вопрос 3. Определители 2-го и 3-го порядка
- •Вопрос 4 Определители n-го порядка.
- •Вопрос 5. Понятие минора и алгебраического дополнения.
- •Вопрос 6. N-мерные векторы, операции над ними.
- •Вопрос 7 Понятие эн-мерного векторного пространства. Линейная зависимость вектора.
- •Вопрос 10. Ранг матрицы.
- •Вопрос 8. Определение ранга матрицы
- •Вопрос 9.10.11
- •Вопрос 12.Обратная матрица
- •Вопрос 15. Плоскость. Взаимное расположение плоскостей.
- •Вопрос 16. Взаимное расположение прямой и плоскости в пространстве.
- •Вопрос 17. Основные понятия и свойства функций
- •Вопрос 18.Понятие элементарной функции и их классификация.
- •Вопрос 19.Числовая последовательность и её пределы.
- •Вопрос 20. Предел функции основные понятия о пределах. Понятие бесконечно малых и бесконечно больших величин
- •Вопрос 24. Правила дифференцирования
- •25. Производная основный элементарных функций. Таблица производных
- •Вопрос 26. Понятие Дифференциала и его свойства. (продолжение вопрос 24)
- •Вопрос 27. Теорема о промежуточном значении.
- •Вопрос28.Применение производной в исследовании функций
- •Вопрос 29:Понятие экстремума функции
- •Вопрос 30. Выпуклые функции.
- •Вопрос 33.
- •Вопрос 34. Экстремумы функций нескольких переменных. (Не весь)
- •Вопрос 36 Методы интегрирования.
- •Вопрос 37. Определенный интеграл Римана, Дарбу, Ньютона-Лейбница, виды интегрируемых функций.
- •Вопрос 39 Несобственные интегралы
Вопрос 37. Определенный интеграл Римана, Дарбу, Ньютона-Лейбница, виды интегрируемых функций.
В
школе к понятию определенного интеграла
нас подводили рассмотрением задачи о
вычислении площади криволинейной
трапеции. Рассматривалась непрерывная
неотрицательная функция y
= f(x) на
отрезке [a;
b],
этот отрезок разбивался на n равных
частей точками ![]() ,
и соответствующая площадь криволинейной
трапеции приближенно представлялась
суммой площадей элементарных
прямоугольников
,
и соответствующая площадь криволинейной
трапеции приближенно представлялась
суммой площадей элементарных
прямоугольников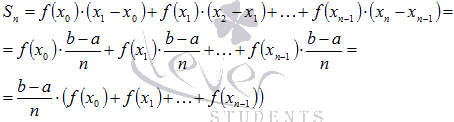
Далее
делалось предположение, что значение
этого выражения стремиться к некоторому
числу ![]() при
бесконечном увеличении количества
точек разбиения отрезка[a;
b].
В итоге это предположение обобщали для
любой непрерывной на отрезке функции y
= f(x) (не
обязательно неотрицательной) и
число
при
бесконечном увеличении количества
точек разбиения отрезка[a;
b].
В итоге это предположение обобщали для
любой непрерывной на отрезке функции y
= f(x) (не
обязательно неотрицательной) и
число ![]() назвалиопределенным
интегралом.
Можно сказать, что к понятию определенного
интеграла в школе мы подходили в
геометрическом смысле.
назвалиопределенным
интегралом.
Можно сказать, что к понятию определенного
интеграла в школе мы подходили в
геометрическом смысле.
В этой статье мы сначала рассмотрим определения определенного интеграла, данные Риманом и Дарбу, также покажем, что подразумевается под определенным интегралом в смысле Ньютона-Лейбница. После этого озвучим необходимое условие интегрируемости функции на отрезке и перечислим виды интегрируемых функций.
Навигация по странице.
Определенный интеграл Римана.
Определенный интеграл Дарбу.
Определенный интеграл Ньютона-Лейбница.
Необходимое условие интегрируемости функции на отрезке, виды интегрируемых функций.
Определенный интеграл Римана.
Рассмотрим
функцию y
= f(x),
которая определена на отрезке [a;
b].
Разобьем отрезок [a;
b] наn частей ![]() точками
точками![]() .
.
Обозначим ![]() ,
а точки
,
а точки![]() будем
выбирать так, чтобы
будем
выбирать так, чтобы![]() при
при![]() .
Внутри каждого отрезка
.
Внутри каждого отрезка![]() выберем
точку
выберем
точку![]() .
.
При
озвученных условиях существует множество
способов выбора точек ![]() и
и![]() .
.
Интегральной
суммой функции y
= f(x) для
данного разбиения отрезка [a;
b] и
данного выбора точек ![]() называют
выражение
называют
выражение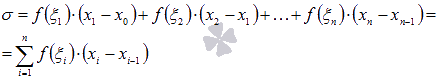
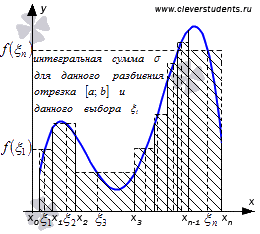
Для
конкретного разбиения отрезка [a;
b] и
выбора точек ![]() мы
получим свою интегральную сумму. То
есть, мы имеем множество интегральных
сумм для различных вариантов выбора
мы
получим свою интегральную сумму. То
есть, мы имеем множество интегральных
сумм для различных вариантов выбора![]() и
и![]() .
.
Число ![]() называетсяпределом
интегральных сумм
называетсяпределом
интегральных сумм ![]() при
при![]() ,
если для любого сколь угодно малого
положительного ипсилон
,
если для любого сколь угодно малого
положительного ипсилон![]() существует
такое сколь угодно малое положительное,
зависящее от ипсилон, дельта
существует
такое сколь угодно малое положительное,
зависящее от ипсилон, дельта![]() ,
что как только
,
что как только![]() ,
то при любом выборе точек
,
то при любом выборе точек![]() справедливо
неравенство
справедливо
неравенство![]() .
.
Функция y
= f(x) называется интегрируемой
на отрезке [a;
b],
если существует конечный предел ее
интегральных сумм при ![]() .
Значение предела естьопределенный
интеграл Римана.
.
Значение предела естьопределенный
интеграл Римана.
Принято
следующее обозначение интеграла
Римана: 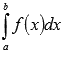 .
Тогда по определению определенного
интеграла Римана имеем
.
Тогда по определению определенного
интеграла Римана имеем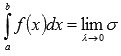 .
.
Числа a и b называются нижним и верхним пределом интегрирования соответственно, f(x)называется подынтегральной функцией, x – переменной интегрирования.
Значение
определенного интеграла Римана не
зависит от переменной интегрирования,
то есть,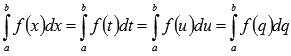 .
.
К началу страницы
Определенный интеграл Дарбу.
Для понимания необходимого и достаточного условия существования определенного интеграла Дарбу нам потребуется несколько дополнительных определений.
Рассмотрим
ограниченную на отрезке [a;
b] функцию y
= f(x).
Вновь разобьем отрезок [a;
b]на n частей
точками ![]() при
прежнем условии
при
прежнем условии![]() при
при![]() .
Пусть
.
Пусть![]() и
и![]() -точная
нижняя и точная верхняя грань
множества значений
функцииy
= f(x) на i-ом
отрезке,
-точная
нижняя и точная верхняя грань
множества значений
функцииy
= f(x) на i-ом
отрезке, ![]() .
Для непрерывной и ограниченной функции
.
Для непрерывной и ограниченной функции![]() .
.
Выражения
вида
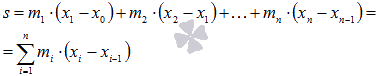 и
и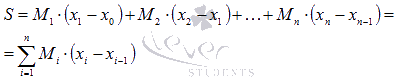 для
данного разбиения отрезка[a;
b] называют нижней
и верхней суммами Дарбусоответственно.
для
данного разбиения отрезка[a;
b] называют нижней
и верхней суммами Дарбусоответственно.
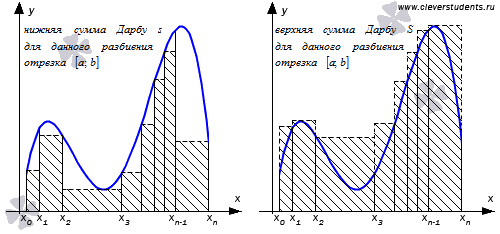
Очевидно,
что для фиксированного разбиения
отрезка [a;
b] справедливо
двойное неравенство ![]() .
Другими словами,s и S –
точная нижняя и точная верхняя грань
множества интегральных сумм соответственно.
.
Другими словами,s и S –
точная нижняя и точная верхняя грань
множества интегральных сумм соответственно.
Для
интегрируемости ограниченной на
отрезке [a;
b] функции y
= f(x) необходимо
и достаточно, чтобы предел разности
верхней и нижней сумм Дарбу был равен
нулю при ![]() ,
то есть, чтобы выполнялось условие
,
то есть, чтобы выполнялось условие![]() .
Это условие есть необходимое и достаточное
условие существования определенного
интеграла Дарбу, а определенный интеграл,
рассмотренный в смысле озвученного
условия, называютопределенным
интегралом Дарбу.
.
Это условие есть необходимое и достаточное
условие существования определенного
интеграла Дарбу, а определенный интеграл,
рассмотренный в смысле озвученного
условия, называютопределенным
интегралом Дарбу.
Определенный
интеграл Дарбу обозначают также, как и
интеграл Римана, то есть, 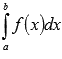 .
.
К началу страницы
Определенный интеграл Ньютона-Лейбница.
Сейчас покажем, как дается понятие определенного интеграла Ньютона-Лейбница.
Пусть
функция y=f(x) имеет
первообразную F(x) на
отрезке [a;
b],
причем значение первообразной в
точке x=a равно
нулю: F(a)=0. Определенным
интегралом Ньютона-Лейбница называется
значение этой первообразной в точке b,
то есть, 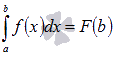 приF(a)=0.
приF(a)=0.
Это
определение тесно связано с формулой
Ньютона-Лейбница  .
В формуле Ньютона-ЛейбницаF(x) –
любая первообразная из их множества, а
в понятии определенного интеграла
Ньютона-Лейбница фигурирует именно та
первообразная, которая обращается в
ноль при x=a.
.
В формуле Ньютона-ЛейбницаF(x) –
любая первообразная из их множества, а
в понятии определенного интеграла
Ньютона-Лейбница фигурирует именно та
первообразная, которая обращается в
ноль при x=a.
Вопрос
38. Методы интегрирования. 1. По замене.
Для
упрощения подынтегральной функции и,
тем самым, для нахождения интеграла
![]() часто применяется так называемая
подстановка или замена переменных.Например:
1.
часто применяется так называемая
подстановка или замена переменных.Например:
1.
![]() .
Если применить замену
.
Если применить замену![]() ;
;![]() ,
то получим:
,
то получим:![]()
2.![]() .
Применим замену
.
Применим замену![]() ;
;![]() .
В результате получим:
.
В результате получим:![]()
Наряду с заменой переменных часто применяется метод разложения, который опирается на линейные свойства интегралов. Это можно проиллюстрировать следующим примером:
![]()
![]()
2.По
частям. Если
функции
![]() и
и![]() дифференцируемы на множестве
дифференцируемы на множестве![]() и, кроме того, на этом множестве существует
интеграл
и, кроме того, на этом множестве существует
интеграл![]() ,
то на нем существует и интеграл
,
то на нем существует и интеграл![]() ,
причем
,
причем![]() .Действительно,
если проинтегрировать формулу нахождения
дифференциала произведения двух функций
.Действительно,
если проинтегрировать формулу нахождения
дифференциала произведения двух функций
![]() ,
то можно получить следующее соотношение
между первообразными от этих функций:
,
то можно получить следующее соотношение
между первообразными от этих функций:
![]() .
Такой способ нахождения интеграла
называетсяинтегрированием
по частям.
Этот
способ целесообразно применять, если
интеграл, стоящий в правой части проще
исходного. При использовании метода
интегрирования по частям задана левая
часть равенства, т.е. функция
.
Такой способ нахождения интеграла
называетсяинтегрированием
по частям.
Этот
способ целесообразно применять, если
интеграл, стоящий в правой части проще
исходного. При использовании метода
интегрирования по частям задана левая
часть равенства, т.е. функция
![]() и дифференциал
и дифференциал![]() .
Таким образом, выбор функций
.
Таким образом, выбор функций![]() и
и
![]() неоднозначен, причем не каждый способ
выбора этих функций ведет к упрощению
первоначального интеграла. Функции,
интегрируемые по частям, можно схематично
разделить на три группы.
неоднозначен, причем не каждый способ
выбора этих функций ведет к упрощению
первоначального интеграла. Функции,
интегрируемые по частям, можно схематично
разделить на три группы.
1.
Интегралы, подынтегральная функция
которых содержит в качестве множителя
одну из следующих функций:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
при условии, что оставшаяся часть
подынтегральной функции представляет
собой производную известной функции.
,
при условии, что оставшаяся часть
подынтегральной функции представляет
собой производную известной функции.

В
случае если подынтегральная функция
содержит в качестве множителя одну из
перечисленных выше функций в степени
![]() ,
то операцию интегрирования по частям
придется повторять
,
то операцию интегрирования по частям
придется повторять![]() раз.
раз.
2.
Интегралы, подынтегральная функция
которых содержит в качестве множителя
одну из следующих функций:
![]() ,
,![]() ,
,![]() ,a
также, полином
,a
также, полином
![]() й
степени
й
степени![]() :
: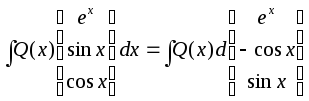 .
.
Для
вычисления интегралов второй группы
нужно формулу интегрирования по частям
применять
![]() раз, причем в качестве функции
раз, причем в качестве функции![]() нужно брать многочлен соответствующей
степени. После каждого интегрирования
степень полинома будет понижаться на
единицу.
нужно брать многочлен соответствующей
степени. После каждого интегрирования
степень полинома будет понижаться на
единицу.
3.
Интегралы вида:
![]() ;
;![]() ;
;![]() .
.
Применение формулы интегрирования по частям может привести к ситуации, когда интеграл в правой части и интеграл в левой части равенства совпадают, т.е. получается равенство вида:
![]() ,
где
,
где ![]() исходный интеграл;
исходный интеграл;![]() постоянная
постоянная![]() .В
этом случае применение метода
интегрирования по частям позволяет
получить уравнение первого порядка для
.В
этом случае применение метода
интегрирования по частям позволяет
получить уравнение первого порядка для![]() ,
из решения которого находится исходный
интеграл
,
из решения которого находится исходный
интеграл![]() :
:![]() .
.
3.Дробнорациональные
выражения. При
интегрировании правильной рациональной
дроби производится разложение этой
дроби на простейшие, для чего предварительно
разлагается на элементарные множители
многочлен
![]() .
Коэффициенты разложения определяются
методом неопределенных множителей. По
членное интегрирование результатов
разложения сводится к вычислению
интегралов вида:
.
Коэффициенты разложения определяются
методом неопределенных множителей. По
членное интегрирование результатов
разложения сводится к вычислению
интегралов вида:![]() и
и![]() .
Интегралы вида
.
Интегралы вида![]() вычисляются следующим образом:
вычисляются следующим образом:![]() ;
;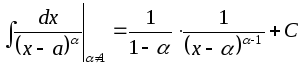 ;
;
Вычисление
 .
Во многих случаях интегрирование
иррациональной функции удается выполнить,
применив замену переменной интегрирования,
преобразующую подынтегральную функцию
в рациональную. Если
.
Во многих случаях интегрирование
иррациональной функции удается выполнить,
применив замену переменной интегрирования,
преобразующую подынтегральную функцию
в рациональную. Если
![]() рациональная
функция своих аргументов, а
рациональная
функция своих аргументов, а![]() целые положительные числа, то интеграл:
целые положительные числа, то интеграл:![]() приводится к интегралу от рациональной
функции при помощи подстановки
приводится к интегралу от рациональной
функции при помощи подстановки![]() ,
где
,
где![]() наибольшее
общее кратное показателей корней
наибольшее
общее кратное показателей корней![]() .Сходная
подстановка рационализирует подынтегральную
функцию и в более общем случае
интегрирования выражений типа:
.Сходная
подстановка рационализирует подынтегральную
функцию и в более общем случае
интегрирования выражений типа:
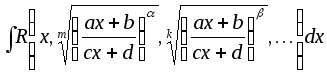 .
В этом случае также применяется
подстановка
.
В этом случае также применяется
подстановка
![]() ,
где, как и в рассмотренном выше случае,
,
где, как и в рассмотренном выше случае,![]() наибольшее
общее кратное показателей корней
наибольшее
общее кратное показателей корней![]() .
.
Вычисление
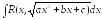 .
Интеграл
.
Интеграл
![]() сводится к интегралу от рациональной
функции с помощью одной из следующих
подстановок:
сводится к интегралу от рациональной
функции с помощью одной из следующих
подстановок:
Если
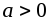 ,
то
,
то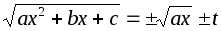 ;
;Если
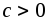 ,
то
,
то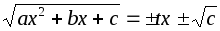 ;
;Если
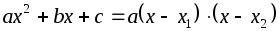 ,
,
то
![]() .
Здесь
.
Здесь![]() - новая переменная. Интеграл
- новая переменная. Интеграл![]() находится подстановкой
находится подстановкой![]() .
Интеграл
.
Интеграл
![]() находится подстановкой
находится подстановкой![]() .
Интеграл
.
Интеграл
![]() находится подстановкой
находится подстановкой![]() .
.
Вычисление
 .Интеграл
.Интеграл
![]() ,
где
,
где![]() - рациональная функция, всегда сводится
к интегралу от рациональной функции
при помощи универсальной подстановки
- рациональная функция, всегда сводится
к интегралу от рациональной функции
при помощи универсальной подстановки![]() .
При этом:
.
При этом:![]() .
.
При
вычислении таких интегралов можно
использовать также и специальные
подстановки, а именно: в случае, когда
![]() ,
можно использовать подстановку
,
можно использовать подстановку![]() .
.
В
случае неопределенного интеграла вида
![]() это соответствует нечетному значению
это соответствует нечетному значению![]() .
Если
.
Если
![]() ,
можно
использовать подстановку
,
можно
использовать подстановку
![]() .
Если
.
Если![]() ,
то можно использовать подстановку
,
то можно использовать подстановку![]() .
.
Вычисление
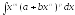 .
Интеграл от дифференциального бинома,
т.е. интеграл
.
Интеграл от дифференциального бинома,
т.е. интеграл
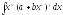 ,
где
,
где![]() рациональные числа,
рациональные числа,![]() и
и![]() постоянные, отличные от нуля, сводится
к интегралу от рациональной функции в
трех случаях:
постоянные, отличные от нуля, сводится
к интегралу от рациональной функции в
трех случаях:
когда
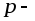 целое число, – разложением на слагаемые
по формуле бинома Ньютона;
целое число, – разложением на слагаемые
по формуле бинома Ньютона;когда
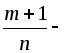 целое число, – подстановкой
целое число, – подстановкой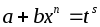 ,
где
,
где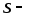 знаменатель дроби
знаменатель дроби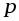 ;
;когда
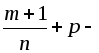 целое число, – подстановкой
целое число, – подстановкой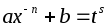 .
.
Как
мы видим, не существует сколько-нибудь
общих приемов нахождения неопределенных
интегралов от любой элементарной
функции. Более того, доказано, что многие,
порой очень простые на первый взгляд,
интегралы не выражаются через элементарные
функции, или, как говорят, не берутся.
Например, к таким интегралам относятся:
![]() .
.
4.Трегонометрические.
1.Интегралы
типа
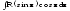 удобно вычислять с помощью подстановки
удобно вычислять с помощью подстановки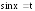 .
Тогда
.
Тогда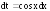 и получаем простой интеграл
и получаем простой интеграл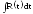 .
.
2.
Интегралы типа
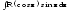 удобно вычислять с помощью подстановки
удобно вычислять с помощью подстановки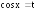 .
Тогда
.
Тогда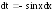 и интеграл приводится к виду
и интеграл приводится к виду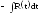 .
.
3.
Если подынтегральная функция зависит
только от
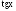 (
(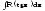 ),
то удобна замена
),
то удобна замена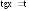 .
В этом случае
.
В этом случае и
и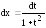 .
В результате получаем
.
В результате получаем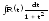 .
.
4.
Если подынтегральная функция является
рациональной относительно четных
степеней
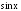 и
и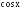 ,
то есть
,
то есть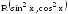 ,
то в этом случае также удобна замена
,
то в этом случае также удобна замена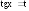 .
При этом:
.
При этом:
 ;
;
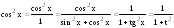 ;
;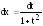 .
.
Данная подстановка в этом случае дает более простую рациональную дробь, чем с использованием универсальной тригонометрической подстановки.
Пусть
дан интеграл
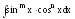 ,
где
,
где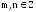 и при этом хотя бы одно из этих чисел
нечетное. Допустим, что
и при этом хотя бы одно из этих чисел
нечетное. Допустим, что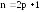 .
Тогда
.
Тогда
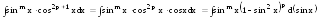 .
.
Далее
делается замена
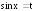 ,
и получаем
,
и получаем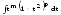 .
.
6.
Пусть дан интеграл
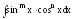 ,
где
,
где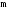 и
и неотрицательные и четные. Положим, что
неотрицательные и четные. Положим, что ,
,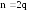 .
Тогда
.
Тогда
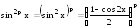 ;
;
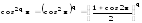 .
.
Данная
замена позволяет в два раза понизить
степень тригонометрических функций.
Раскрывая скобки в интеграле
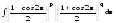 ,
получаем снова случаи 5 или 6.
,
получаем снова случаи 5 или 6.
7.
Пусть дан
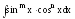 ,
где
,
где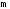 и
и – четные и хотя бы одно из этих чисел
отрицательно. Тогда удобна та же замена,
что и в случае 4.
– четные и хотя бы одно из этих чисел
отрицательно. Тогда удобна та же замена,
что и в случае 4.
8.
В случае
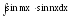 используется тригонометрическая формула
используется тригонометрическая формула
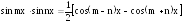 и
интеграл превращается в два табличных
интеграла.
и
интеграл превращается в два табличных
интеграла.
9.
В случае
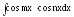 используется тригонометрическая формула
используется тригонометрическая формула
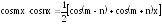 .
.
10.В
случае
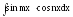 используется тригонометрическая формула
используется тригонометрическая формула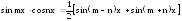
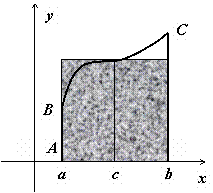
Определенный
интеграл и его свойства. Приложения
(вычисление площади криволинейной
трапеции). Вычисление
площади криволинейной трапеции.
Пусть на отрезке [a,b]
(b>a)
задана непрерывная функция y
= f(x)
, принимающая на этом отрезке неотрицательные
значения :
![]() при
при![]() .
Требуется определить площадьS
криволинейной трапеции ABCD,
ограниченной снизу отрезком [a,b],
слева и справа - прямыми x
= a
и x
= b,
сверху – функцией y
= f(x).
.
Требуется определить площадьS
криволинейной трапеции ABCD,
ограниченной снизу отрезком [a,b],
слева и справа - прямыми x
= a
и x
= b,
сверху – функцией y
= f(x).
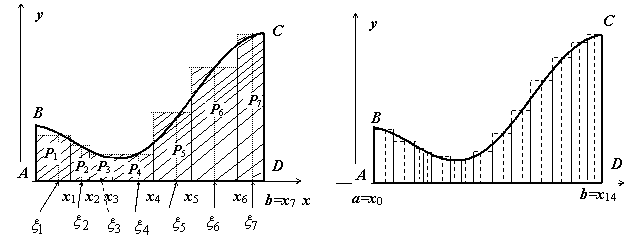
![]() Для
решения этой задачи разделим произвольным
образом основаниеAD
фигуры точками x0
=
a,
x1
,
x2
,
…, xn-1
= a,
xn
= b
на n
частей [x0
,
x1],
[x1
,
x2],
…, [xi-1
,
xi],
…, [xn-1
,
xn];
символом
Для
решения этой задачи разделим произвольным
образом основаниеAD
фигуры точками x0
=
a,
x1
,
x2
,
…, xn-1
= a,
xn
= b
на n
частей [x0
,
x1],
[x1
,
x2],
…, [xi-1
,
xi],
…, [xn-1
,
xn];
символом
![]() будем
обозначать длинуi-го
отрезка:
будем
обозначать длинуi-го
отрезка:
![]() .
На каждом из отрезков [xi-1
,
xi]
выберем произвольную точку
.
На каждом из отрезков [xi-1
,
xi]
выберем произвольную точку
![]() ,
найдём
,
найдём![]() ,
вычислим произведение
,
вычислим произведение![]() и просуммируем эти произведения по всем
прямоугольникам. Полученную сумму
обозначимS
ступ:
и просуммируем эти произведения по всем
прямоугольникам. Полученную сумму
обозначимS
ступ:
![]() .
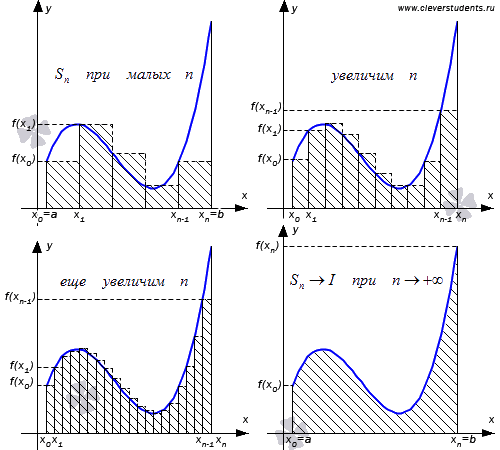
.![]() Sступ
равно площади ступенчатой фигуры,
образованной прямоугольниками Pi
, i
= 1,2,…,n;
на левом рисунке эта площадь заштрихована.
Sступ
не равна искомой площади S,
она только даёт некоторое приближение
к S.
Для того, чтобы улучшить это приближение,
будем увеличивать количество n
отрезков таким образом, чтобы максимальная
длина этих отрезков
Sступ
равно площади ступенчатой фигуры,
образованной прямоугольниками Pi
, i
= 1,2,…,n;
на левом рисунке эта площадь заштрихована.
Sступ
не равна искомой площади S,
она только даёт некоторое приближение
к S.
Для того, чтобы улучшить это приближение,
будем увеличивать количество n
отрезков таким образом, чтобы максимальная
длина этих отрезков
![]() стремилась
к нулю (на рисунке ступенчатые фигуры
изображены приn
= 7 (слева) и при n
= 14 (справа)). При
стремилась
к нулю (на рисунке ступенчатые фигуры
изображены приn
= 7 (слева) и при n
= 14 (справа)). При![]() разница
междуSступ
и S
будет тоже стремиться к нулю, т.е.
разница
междуSступ
и S
будет тоже стремиться к нулю, т.е.
 .
.
Определение определённого интеграла. Пусть на отрезке [a,b] задана функция y = f(x). Разобьём отрезок [a,b] произвольным образом на n частей точками [x0 , x1], [x1 , x2], …, [xi-1 , xi], …, [xn-1 , xn]; длину i-го отрезка обозначим:
![]() ;
максимальную из длин отрезков обозначим
;
максимальную из длин отрезков обозначим
![]() .
На каждом из отрезков [xi-1
,
xi]
выберем произвольную точку
.
На каждом из отрезков [xi-1
,
xi]
выберем произвольную точку
![]() и
составим сумму
и
составим сумму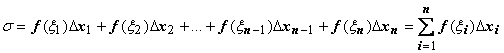 .
Сумма
.
Сумма![]() называется
интегральной суммой. Если существует
(конечный) предел последовательности
интегральных сумм
называется
интегральной суммой. Если существует
(конечный) предел последовательности
интегральных сумм![]() при
при![]() ,
не зависящий ни от способа разбиения
отрезка [a,b]
на части [xi-1
,
xi],
ни от выбора точек
,
не зависящий ни от способа разбиения
отрезка [a,b]
на части [xi-1
,
xi],
ни от выбора точек
![]() ,
то функцияf(x)
называется интегрируемой по отрезку
[a,b],
а этот предел называется определённым
интегралом от функции f(x)
по отрезку [a,b]
и обозначается
,
то функцияf(x)
называется интегрируемой по отрезку
[a,b],
а этот предел называется определённым
интегралом от функции f(x)
по отрезку [a,b]
и обозначается
![]() .
Функцияf(x),
как и в случае неопределённого интеграла,
называется подынтегральной, числа a
и b
- соответственно, нижним и верхним
пределами интегрирования.
.
Функцияf(x),
как и в случае неопределённого интеграла,
называется подынтегральной, числа a
и b
- соответственно, нижним и верхним
пределами интегрирования.
![]() Кратко
определение иногда записывают так:
Кратко
определение иногда записывают так:![]()
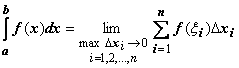 .
.![]() В
этом определении предполагается, чтоb>
a.
Для других случаев примем, тоже по
определению:
Если b=a,
то
В
этом определении предполагается, чтоb>
a.
Для других случаев примем, тоже по
определению:
Если b=a,
то
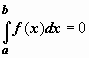 ;
еслиb<a,
то
;
еслиb<a,
то
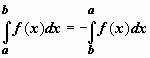 .
.
Свойства
определённого интеграла.1.
Линейность.
Если функции y
= f(x),
y
= g(x)
интегрируемы по отрезку [a,b]
, то по этому отрезку интегрируема их
линейная комбинация A
f(x)
+ B
g(x)
(A,
B
= const), и
![]()
![]() .
Док-во:
для любого разбиения отрезка и любого
выбора точек
.
Док-во:
для любого разбиения отрезка и любого
выбора точек
![]() выполняется
выполняется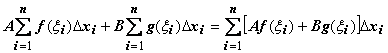 .
Перейдем в этом равенстве к пределу при
.
Перейдем в этом равенстве к пределу при![]() .
Так как существуют пределы интегральных
сумм, стоящих в левой части равенства,
то существует предел линейной комбинации
этих сумм, следовательно, существует
предел правой интегральной суммы, откуда
следует истинность и утверждения, и
равенства.
2.
Аддитивность.
Если y
= f(x)
интегрируема по отрезку [a,b]
и точка c
принадлежит этому отрезку, то
.
Так как существуют пределы интегральных
сумм, стоящих в левой части равенства,
то существует предел линейной комбинации
этих сумм, следовательно, существует
предел правой интегральной суммы, откуда
следует истинность и утверждения, и
равенства.
2.
Аддитивность.
Если y
= f(x)
интегрируема по отрезку [a,b]
и точка c
принадлежит этому отрезку, то
![]()
![]() .
Док-во.
Если f(x)
удовлетворяет условиям интегрируемости
по отрезку [a,b],
то она удовлетворяет условиям
интегрируемости по отрезкам [a,c]
и [c,b].
Будем брать такие разбиения отрезка
[a,b]
, чтобы точка c
являлась одним из узлов xi:
c
= xi0,
. Тогда
.
Док-во.
Если f(x)
удовлетворяет условиям интегрируемости
по отрезку [a,b],
то она удовлетворяет условиям
интегрируемости по отрезкам [a,c]
и [c,b].
Будем брать такие разбиения отрезка
[a,b]
, чтобы точка c
являлась одним из узлов xi:
c
= xi0,
. Тогда
![]() .
В этом равенстве первая сумма справа -
интегральная сумма для
.
В этом равенстве первая сумма справа -
интегральная сумма для![]() ,
вторая - для
,
вторая - для![]() .
Переходим к пределу при
.
Переходим к пределу при![]() .
Пределы для всех трёх сумм существуют,
и
.
Пределы для всех трёх сумм существуют,
и![]() .
Свойство аддитивности остаётся верным
при любом расположении точек, если
только функция интегрируема по самому
широкому интервалу. Пусть, например,c
< b
< a,
и f(x)
интегрируема по [c,
a].
Тогда, по доказанному,
.
Свойство аддитивности остаётся верным
при любом расположении точек, если
только функция интегрируема по самому
широкому интервалу. Пусть, например,c
< b
< a,
и f(x)
интегрируема по [c,
a].
Тогда, по доказанному,
![]() .
Отсюда и из определения интеграла для
случая, когда нижний предел больше
верхнего, следует, что
.
Отсюда и из определения интеграла для
случая, когда нижний предел больше
верхнего, следует, что![]() .
При формулировании и доказательстве
следующих свойств предполагаем, что b
> a.
3.
Интеграл от единичной функции (
f(x)
= 1).
Если
f(x)
= 1,
то
.
При формулировании и доказательстве
следующих свойств предполагаем, что b
> a.
3.
Интеграл от единичной функции (
f(x)
= 1).
Если
f(x)
= 1,
то
![]() .
.
![]() Док-во.
Если
f(x)
= 1 , то для любого разбиения
Док-во.
Если
f(x)
= 1 , то для любого разбиения
![]() =xn
-
x0
= b
– a,
т.е любая интегральная сумма равна длине
отрезка. Предел постоянной равен этой
постоянной, откуда и следует доказываемое
утверждение.
4.
Теорема об интегрировании неравенств.
Если в любой точке
=xn
-
x0
= b
– a,
т.е любая интегральная сумма равна длине
отрезка. Предел постоянной равен этой
постоянной, откуда и следует доказываемое
утверждение.
4.
Теорема об интегрировании неравенств.
Если в любой точке
![]() выполняется
неравенство
выполняется
неравенство![]() ,
и функцииf(x),
g(x)
интегрируемы по отрезку [a,b],
то
,
и функцииf(x),
g(x)
интегрируемы по отрезку [a,b],
то
![]() .
Док-во.
Для любого разбиения отрезка и любого
выбора точек
.
Док-во.
Для любого разбиения отрезка и любого
выбора точек
![]() при
при![]()
![]() .
Переходя в этом неравенстве к пределу
при
.
Переходя в этом неравенстве к пределу
при![]() ,
получаем требуемое неравенство.
5.
Теоремы об оценке интеграла.
5.1.
Если на отрезке [a,b]
функция удовлетворяет неравенству
,
получаем требуемое неравенство.
5.
Теоремы об оценке интеграла.
5.1.
Если на отрезке [a,b]
функция удовлетворяет неравенству
![]() ,
то
,
то![]() .Док-во.
Докажем левое неравенство (цифрами над
знаками импликации обозначены номера
применяемых ранее доказанных свойств):
.Док-во.
Докажем левое неравенство (цифрами над
знаками импликации обозначены номера
применяемых ранее доказанных свойств):
![]() .
Аналогично доказывается и правое
неравенство.
5.2.
Если функция f(x)
интегрируема по отрезку [a,b],
то
.
Аналогично доказывается и правое
неравенство.
5.2.
Если функция f(x)
интегрируема по отрезку [a,b],
то
![]() .
.
![]()
![]() Док-во.
Док-во.
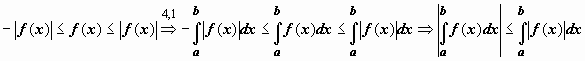 .
6.
Теорема о среднем.
Если f(x)
непрерывна на отрезке [a,b],
то существует точка
.
6.
Теорема о среднем.
Если f(x)
непрерывна на отрезке [a,b],
то существует точка
![]() ,
такая что
,
такая что .
.
![]() Док-во.
Функция, непрерывная на отрезке, принимает
на этом отрезке своё наименьшее m
и наибольшее M
значения. Тогда
Док-во.
Функция, непрерывная на отрезке, принимает
на этом отрезке своё наименьшее m
и наибольшее M
значения. Тогда
![]() .
Число
.
Число![]() заключено
между минимальным и максимальным
значениями функции на отрезке. Одно из
свойств функции, непрерывной на отрезке,
заключается в том, что эта функция
принимает любое значение, расположенное
междуm
и M.
Таким образом, существует точка
заключено
между минимальным и максимальным
значениями функции на отрезке. Одно из
свойств функции, непрерывной на отрезке,
заключается в том, что эта функция
принимает любое значение, расположенное
междуm
и M.
Таким образом, существует точка
![]() ,
такая что
,
такая что![]() .
.![]() Это
свойство имеет простую геометрическую
интерпретацию: если
Это
свойство имеет простую геометрическую
интерпретацию: если![]() непрерывна
на отрезке [a,b],
то существует точка
непрерывна
на отрезке [a,b],
то существует точка
![]() такая,
что площадь криволинейной трапецииABCD
равна площади прямоугольника с основанием
[a,b]
и высотой f(c)
(на рисунке выделен цветом).
такая,
что площадь криволинейной трапецииABCD
равна площади прямоугольника с основанием
[a,b]
и высотой f(c)
(на рисунке выделен цветом).