Вопрос 33.

Полный дифференциал - линейная часть приращения функции.

Математическое определение Править

Пусть полное приращение функции функцииможно разложить на сумму двух членов:

,

где коэффициенты A, B и C не зависят от , аи имеет высший порядок относительно расстояния.

Тогда первый член

называется полным дифференциалом функции и обозначается

. Дифференцируемость функции. Пусть . Составимполное приращение функции в точке:

.

         Определение. Функция называетсядифференцируемой в точке , если ее полное приращение в этой точке можно представить в виде

,                                  (1)

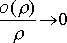где и– некоторые числа,при,.

         Другими словами, функция дифференцируема в точке, если ее приращениеэквивалентно функции:при. Выражениев этом случае представляет собой главную часть приращения, линейно зависящую оти.

         Определение. Если функция дифференцируема в точке, то главную линейную частьее приращенияназываютполным дифференциалом в точке и обозначают в виде

.

         Для независимых переменных иполагаюти. Поэтому полный дифференциал записывают также в виде

.

         Формула (1) показывает, что, как и в случае функции одной переменной, верна

         Теорема 5. Если функция дифференцируема в точке, то она непрерывна в этой точке.

         Обратное утверждение неверно, т.е. непрерывность является только необходимым, но не достаточным условием дифференцируемости функции. Покажем это.

         Пример.  Найдем частные производные функции:

.

Полученные формулы теряют смысл в точке .

         Можно показать иначе, что функция не имеет частных производных в точке. В самом деле,. Эта функция одной переменной, как известно, не имеет производной в точке. Последнее и означает, что частная производнаяв точкене существует. Аналогично, не существует частная производная. При этом функция, очевидно, непрерывна в точке. ^

Итак, мы показали, что непрерывная функция может не иметь частных производных. Осталось установить связь между дифференцируемостью и существованием частных производных.

Вопрос 34. Экстремумы функций нескольких переменных. (Не весь)

Определение. Точка называется точкой минимума (максимума) функции , если существует такая окрестность точки , что для всех точек из этой окрестности выполняется неравенство , ( ).

Необходимые условия экстремума. Если – точка экстремума дифференцируемой функции , то ее частные производные и в этой точке равны нулю: . Точки, в которых частные производные первого порядка равны нулю, называются критическими или стационарными. В критических точках функция может иметь экстремум, а может и не иметь.

Достаточное условие экстремума. Пусть функция : а) определена в некоторой окрестности критической точки , в которой и ; б) имеет непрерывные частные производные второго порядка . Тогда, если , то функция в точке имеет экстремум: максимум, если А<0; минимум, если А>0; если , то функция в точке экстремума не имеет. В случае вопрос о наличии экстремума остается открытым.

При исследовании функции двух переменных на экстремум рекомендуется использовать следующую схему:

1.Найти частные производные первого порядка: и .

2.Решить систему уравнений и найти критические точки функции.

3.Найти частные производные второго порядка: , , .

4.Вычислить значения частных производных второго порядка в каждой критической точке и, используя достаточные условия, сделать вывод о наличии экстремума.

5.Найти экстремумы функции.

Вопрос 35. Понятие неопределенного интеграла. Функция называется первообразной для функции, на промежутке, если для каждой точки этого промежутка. Теорема. Если и– любые две первообразные для данной функциина промежутке, то для всехвыполняется равенство.

Доказательство: Таким образом, все семейство первообразных для данной функцииимеет вид, гдеодна из первообразных, апроизвольная постоянная.Совокупность всех первообразных для функции на промежуткеназывается неопределенным интегралом функции. Неопределенный интеграл обозначается следующим образом: , гдезнак интеграла;подынтегральная функция;подынтегральное выражение.

Свойства неопределенного интеграла

1. Производная неопределенного интеграла равна подынтегральной функцией:,

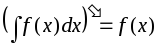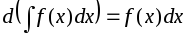
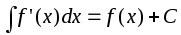2. Эти свойства означают, что интегрирование и дифференцирование – взаимно обратные операции.

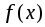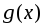3. Если и– интегрируемые функции, т.е. на промежутке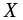они имеют первообразные, то сумма функций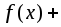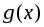также интегрируема и.

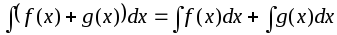4. Если 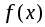– интегрируемая функция, а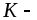постоянная величина, то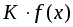– также интегрируемая функция и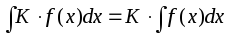.Cвойства 3 и 4 указывают на линейность операции интегрирования: 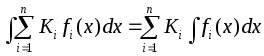, где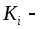постоянные;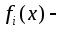интегрируемые функции.

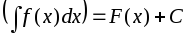5. Если , а также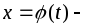дифференцируемая функция, то

.

Простым обращением известных формул дифференцирования элементарных функций получается таблица простейших неопределенных интегралов.

;	;
;	;
;	;
;	;
;	;

Чтобы найти неопределенный интеграл от какой-либо функции, достаточно свести его к одному или нескольким табличным интегралам из вышеприведенной таблицы.