
- •Вопрос 1. Понятие систем линейных уравнений. Их решения.
- •Вопрос 2.Методы решение систем линейных уравнений.
- •Вопрос 3. Определители 2-го и 3-го порядка
- •Вопрос 4 Определители n-го порядка.
- •Вопрос 5. Понятие минора и алгебраического дополнения.
- •Вопрос 6. N-мерные векторы, операции над ними.
- •Вопрос 7 Понятие эн-мерного векторного пространства. Линейная зависимость вектора.
- •Вопрос 10. Ранг матрицы.
- •Вопрос 8. Определение ранга матрицы
- •Вопрос 9.10.11
- •Вопрос 12.Обратная матрица
- •Вопрос 15. Плоскость. Взаимное расположение плоскостей.
- •Вопрос 16. Взаимное расположение прямой и плоскости в пространстве.
- •Вопрос 17. Основные понятия и свойства функций
- •Вопрос 18.Понятие элементарной функции и их классификация.
- •Вопрос 19.Числовая последовательность и её пределы.
- •Вопрос 20. Предел функции основные понятия о пределах. Понятие бесконечно малых и бесконечно больших величин
- •Вопрос 24. Правила дифференцирования
- •25. Производная основный элементарных функций. Таблица производных
- •Вопрос 26. Понятие Дифференциала и его свойства. (продолжение вопрос 24)
- •Вопрос 27. Теорема о промежуточном значении.
- •Вопрос28.Применение производной в исследовании функций
- •Вопрос 29:Понятие экстремума функции
- •Вопрос 30. Выпуклые функции.
- •Вопрос 33.
- •Вопрос 34. Экстремумы функций нескольких переменных. (Не весь)
- •Вопрос 36 Методы интегрирования.
- •Вопрос 37. Определенный интеграл Римана, Дарбу, Ньютона-Лейбница, виды интегрируемых функций.
- •Вопрос 39 Несобственные интегралы
Вопрос 24. Правила дифференцирования
Теорема 1. Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:
(u±v)' = u'±v'
Следствие. Производная конечной алгебраической суммы дифференцируемых функций равна такой же алгебраической сумме производных слагаемых. Например,
(u — v + w)' = u' — v' + w'
Теорема 2. Производная произведения двух дифференцируемых функций равна произведению первой функции на производную второй плюс произведение второй функции на производную первой, т. е.
(uv)' = u'v + uv'
Следствие 1. Постоянный множитель можно выносить за знак производной (cv)' = cv' (с = const).
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждой из них на все остальные.
Например, (uvw)' = u'vw + uv'w + uvw'
Теорема
3. Производная частного двух дифференцируемых
функций определяется формулой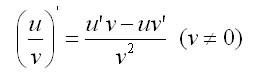
Теорема 4. Если y = f(u) и и = (ф(х)) — дифференцируемые функции своих аргументов, то производная сложной функции у = f (ф(х)) существует и равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной, т. е.
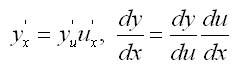
25. Производная основный элементарных функций. Таблица производных
Произво́дная (функции
в точке) — основное понятие дифференциального
исчисления,
характеризующее скорость изменения
функции (в данной точке). Определяется
как предел отношения
приращения функции к приращению
ееаргумента при
стремлении приращения аргумента к нулю,
если такой предел существует. Функцию,
имеющую конечную производную (в некоторой
точке), называют дифференцируемой (в
данной точке).
Вопрос 26. Понятие Дифференциала и его свойства. (продолжение вопрос 24)
Пусть
функция y = f(x) дифференцируема при
некотором значении переменной x .
Следовательно, в точке x существует
конечная производная
![]() ,Тогда
по определению предела функции разность
,Тогда
по определению предела функции разность![]() является
бесконечно малой величиной при х
стремящемуся к нулю.
является
бесконечно малой величиной при х
стремящемуся к нулю.
Выразив
из равенства (1) приращение функции,
получим
![]() .
Если у неравно 0, то в правой части
равенства первое слагаемоеy∆x
линейно относительно ∆х. Поэтому при
∆х стремящемуся к нулю, оно является
бесконечно малой того же порядка малости,
что и ∆х. Второе слагаемое α∆х- бесконечно
малая более высокого порядка малости,
чем первое, так как их отношение α\y
стремится к нулю при ∆x
стремящемуся к нулю.
.
Если у неравно 0, то в правой части
равенства первое слагаемоеy∆x
линейно относительно ∆х. Поэтому при
∆х стремящемуся к нулю, оно является
бесконечно малой того же порядка малости,
что и ∆х. Второе слагаемое α∆х- бесконечно
малая более высокого порядка малости,
чем первое, так как их отношение α\y
стремится к нулю при ∆x
стремящемуся к нулю.
Поэтому
говорят, что первое слагаемое формулы
(2) является главной, линейной относительно
∆х частью приращения функции; чем меньше
∆х , тем большую долю приращения
составляет эта часть. Поэтому при малых
значениях ∆х (и при у не равно 0 ) приращение
функции можно приближенно заменить его
главной частью у∆х , т.е
![]() (3)
(3)
Эту
главную часть приращения функции
называют дифференциалом данной функции
в точке x и обозначают dy,
следовательно
![]()
Дифференциал функции представляет собой преращение ординаты касательной, проведённой к графику функции y=f(x) в данной точке, тогда х получает преращение ∆х.
Свойства
С= const
dC=0
d (U+- Y) = dU+-dY)
d(U*Y)= Y*dU+U*dY
d(U\Y)= Y*dU-U*dY\Y^2
d(CU) = CdU
Рассмотрим сложную функцию y=f(u(x)). Пусть функции y=f(u), u=u(x) дифференцируемы, тогда
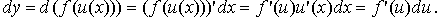
Таким образом, если аргументом функции является функция другого аргумента, то форма дифференциала совпадает с формой дифференциала (7), когда аргументом функции является независимая переменная. Это свойство называется инвариантностью формы дифференциала.
