Вопрос 18.Понятие элементарной функции и их классификация.

После введения в математическую деятельность понятия функции внимание математиков было обращено на изучение большого количества различных функциональных зависимостей. В результате непрерывного развития математики и в настоящее время появляются все новые классы функций.

Среди всего многообразия функций исторически выделились функции, отличающиеся своей простотой и наиболее широкой областью применения. Это так называемые простейшие элементарные функции, основное значение которых состоит в том, что они составляют базу для изучения более сложных функций, являясь в большинстве своем составными элементами последних.

Простейшими элементарными функциями обычно называют линейную (y=kx+b), квадратичную (y=ax2+bx+c), степенную (y=xn, где n целое число, не равно 1), показательную (y=ax,где a больше 0 и не равно 1), логарифмическую (y=loga x, где a больше 0 и не равно 1), тригонометрические (y=sin x, y=cos x, y=tg x, y=ctg x), обратные тригонометрические(y=arcsin x, y=arccos x, y=arctg x, y=arcctg x).

К элементарным функциям относятся основные элементарные функции и те, которые можно образовать из них с помощью конечного числа операций (сложения, вычитания, умножения и деления) и суперпозиций.

Выделим классы функций, которые получены из элементарных:

Целая рациональная функция (или многочлен): y=a0xn+a1xn-1+...+an, где n - целое неотрицательное число (степень многочлена), a0, a1, ..., an - постоянные числа (коэффициенты).

Дробно-рациональная функция, которая является отношением двух целых рациональных функций.

Целые рациональные и дробно-рациональные образуют класс рациональных функций.

Иррациональная функция - это та, которая строится с помощью суперпозиции рациональной функции и степенных функций с рациональными показателями.

Рациональная и иррациональная функции образуют класс алгебраических функций. Алгебраическая функция - произвольная функция y=f(x), которая удовлетворяет уравнению:

A0(x)yn+A1(x)yn-1+...+An-1(x)y+An(x)=0.

Элементарные функции, которые не являются алгебраическими, называются трансцендентными.

Вопрос 19.Числовая последовательность и её пределы.

Числовая последовательность-если по некоторому правилу (закону) в каждом N, числу n поставлено в соответ.вполне определ.число Аn, то говорят, что задана числовая последовательность {An}. {Xn}….

Любая числовая последовательность может быть задана:

1. Пересечением ее элементов а1, а2, а3….аn

2. Аналитический способ: формула n-го члена ( an =(-1)ⁿ 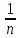где n- N число) и рекурентное соотношение ( указывается 1 элемент последоват. И формула, выражающаю n- член послед.через последующий:

n-1 элемент; а1=3 и аn= 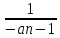- 2 способ.

3.Графически (дискретным множеством точек)

4. Машинный ( таблица простых чисел)

Последоват.явл частным случаем функц.и не редко послед.наз функцией N аргумента=> к послед.применимы понятия монотонности и ограниченности.

Число А наз.пределом последоват. Хn ( A= lim xn. n -∞), если для любого положительного Е найдется такой номер N, что для всех n>N выпоняется неравенство │хn-A│ < E

C ростом номера N элементы послед.хn сколь угодно мало будут отличаться от числа А, а отличаться будут на величину Е ( очень малую).