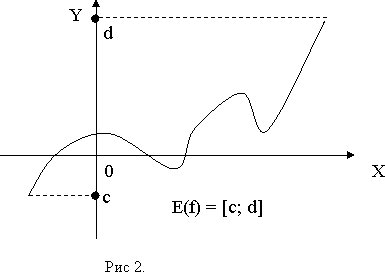- •Вопрос 1. Понятие систем линейных уравнений. Их решения.
- •Вопрос 2.Методы решение систем линейных уравнений.
- •Вопрос 3. Определители 2-го и 3-го порядка
- •Вопрос 4 Определители n-го порядка.
- •Вопрос 5. Понятие минора и алгебраического дополнения.
- •Вопрос 6. N-мерные векторы, операции над ними.
- •Вопрос 7 Понятие эн-мерного векторного пространства. Линейная зависимость вектора.
- •Вопрос 10. Ранг матрицы.
- •Вопрос 8. Определение ранга матрицы
- •Вопрос 9.10.11
- •Вопрос 12.Обратная матрица
- •Вопрос 15. Плоскость. Взаимное расположение плоскостей.
- •Вопрос 16. Взаимное расположение прямой и плоскости в пространстве.
- •Вопрос 17. Основные понятия и свойства функций
- •Вопрос 18.Понятие элементарной функции и их классификация.
- •Вопрос 19.Числовая последовательность и её пределы.
- •Вопрос 20. Предел функции основные понятия о пределах. Понятие бесконечно малых и бесконечно больших величин
- •Вопрос 24. Правила дифференцирования
- •25. Производная основный элементарных функций. Таблица производных
- •Вопрос 26. Понятие Дифференциала и его свойства. (продолжение вопрос 24)
- •Вопрос 27. Теорема о промежуточном значении.
- •Вопрос28.Применение производной в исследовании функций
- •Вопрос 29:Понятие экстремума функции
- •Вопрос 30. Выпуклые функции.
- •Вопрос 33.
- •Вопрос 34. Экстремумы функций нескольких переменных. (Не весь)
- •Вопрос 36 Методы интегрирования.
- •Вопрос 37. Определенный интеграл Римана, Дарбу, Ньютона-Лейбница, виды интегрируемых функций.
- •Вопрос 39 Несобственные интегралы
Вопрос 17. Основные понятия и свойства функций
Ключевые слова: область определения функции, область значений функции четная функция, нечетная функция, периодическая функция. монотонная функция. убывающая функция. возрастающая функция, ограниченная функция.
В элементарной математике изучаются функции только на множестве действительных чисел R. Это значит, что аргумент функции может принимать только те действительные значения, при которых функция определена, т.e.она также принимает только действительные значения.
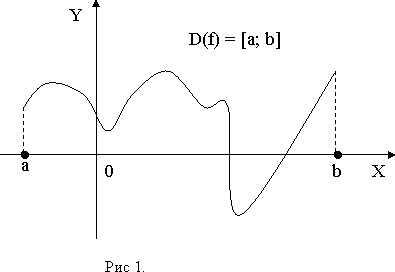
Множество X всех допустимых действительных значений аргументаx, при которых функция y = f (x) определена, называется областью определения функции. Множество Y всех действительных значений y, которые принимает функция,называется областью значений функции.
Теперь можно дать более точное определение функции:
правило(закон) соответствия между множествами X и Y, по которому для каждого элемента из множества X можно найти один и только один элемент из множества Y, называется функцией.
|
|
|
Функция считается заданной, если:
задана область определения функции X ;
задана область значений функции Y ;
известно правило (закон) соответствия, причем такое, что для каждого значения аргумента может быть найдено только одно значение функции. Это требование однозначности функции является обязательным.
Если для любых двух значений аргумента x1и x2 из условия x2 > x1 следует f ( x2 ) > f ( x1 ), то функция f (x ) называетсявозрастающей; если для любых x1 и x2 из условия x2 > x1 следует f (x2)< f (x1),то функция f (x ) называется убывающей. Функция, которая только возрастает или только убывает, называется монотонной.
Функция
называется ограниченной,
если существует такое положительное
число M,
что |f
( x )|![]() M для
всех значений x .
Если
такого числа не существует, то функция
- неограниченная.
M для
всех значений x .
Если
такого числа не существует, то функция
- неограниченная.
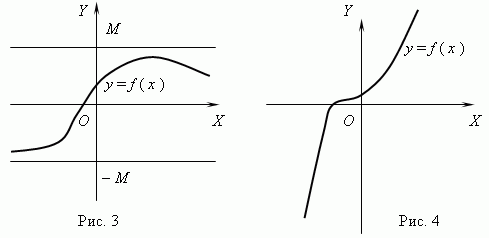
Функция y = f (x) называется непрерывной в точке x = a, если :
функция определена при x = a, т.e. f (a) существует;
существует конечный предел limx
 af(x);
af(x);f (a) = limx
 af(x) .
af(x) .
Если не выполняется хотя бы одно из этих условий, то функция называется разрывной в точке x = a. Если функция непрерывна во всех точках своей области определения, то она называется непрерывной функцией.
Если для любого x из области определения функции имеет место: f ( - x ) = f ( x ), то функция называется чётной; если же имеет место: f (-x) = - f (x), то функция называется нечётной.
График чётной функции симетричен относительно оси Y ( рис.5 ), a график нечётной функции симметричен относительно начала координат ( рис.6 ).
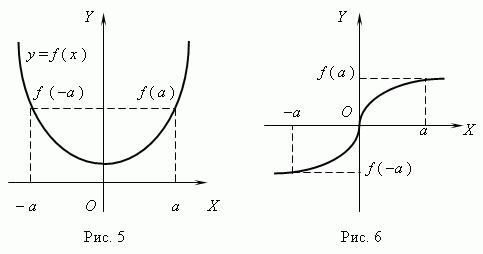
Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f ( x + T ) = f ( x ). Такое наименьшее число называется периодом функции.
Все тригонометрические функции являются периодическими.
Пример
1. Доказать, что sin x имеет период
2![]() .
Решение.
Мы знаем, что sin ( x+ 2
.
Решение.
Мы знаем, что sin ( x+ 2![]() n
) = sin x, где n = 0, ± 1, ± 2, …
Следовательно,
добавление 2
n
) = sin x, где n = 0, ± 1, ± 2, …
Следовательно,
добавление 2![]() n
к аргументу синуса не меняет его
значениe.
Предположим, что P – такое
число, т.e. равенство: sin ( x+ P ) = sin x,
справедливо для любогозначения x.
Но
тогда оно имеет место и при x =
n
к аргументу синуса не меняет его
значениe.
Предположим, что P – такое
число, т.e. равенство: sin ( x+ P ) = sin x,
справедливо для любогозначения x.
Но
тогда оно имеет место и при x =![]() /
2 , т.e. sin (
/
2 , т.e. sin (![]() /
2 + P ) = sin
/
2 + P ) = sin![]() /
2 = 1.
Но по формуле приведения sin
(
/
2 = 1.
Но по формуле приведения sin
(![]() /
2 + P ) = cos P.
Тогда из двух последних
равенств следует, чтоcos P = 1, но мы знаем,
что это верно лишь при P = 2
/
2 + P ) = cos P.
Тогда из двух последних
равенств следует, чтоcos P = 1, но мы знаем,
что это верно лишь при P = 2![]() n.
Так
как наименьшим отличным от нуля числом
из 2
n.
Так
как наименьшим отличным от нуля числом
из 2![]() n
является 2
n
является 2![]() ,
то это число и есть период sin x.
Рассмотрим
sin 2x = sin ( 2x + 2
,
то это число и есть период sin x.
Рассмотрим
sin 2x = sin ( 2x + 2![]() n
) = sin [ 2 ( x +
n
) = sin [ 2 ( x +![]() n
) ] .
Мы видим,что добавление
n
) ] .
Мы видим,что добавление![]() n
к аргументу x, не меняет значение
функции.
Наименьшее отличное от
нуля число из
n
к аргументу x, не меняет значение
функции.
Наименьшее отличное от
нуля число из![]() n
есть
n
есть![]() ,
таким образом, это период sin 2x .
,
таким образом, это период sin 2x .
Значение аргумента, при котором функция равна 0, называется нулём (корнем) функции.
Функция может иметь несколько нулей.
Например, функция y = x (x + 1)(x-3) имеет три нуля: x = 0, x = - 1, x =3.
Геометрически нуль функции – это абсцисса точки пересечения графика функции с осью Х .
На рис.7 представлен график функции с нулями: x = a, x = b и x = c .
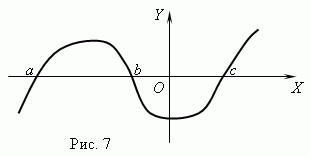
Если график функции неограниченно приближается к некоторой прямой при своём удалении от начала координат, то эта прямая называется асимптотой.