Вопрос 1. Понятие систем линейных уравнений. Их решения.

ЛУ – это уравнение вида:

a_i1х₁+a_i2x₂+a_inx_n=b_it (1), где х₁,х₂…х_n-неизвестные; a_i1,a_i2,a_in-коэффициенты; b_it-свободный член ур-ия.

*только первые степени

*нет соответствующих произведений.

i-номер ур-ия; 1,2…-номер неизвестного.

СЛУ-это: а₁₁х₁ а₁₂х₂… а_1nх_n=b₁

а₂₁х₁ а₂₂х₂… а_2nх_n=b₂

а_m1х₁ а_m2х₂… а_mnх_n=b_m

а₁₁ а₁₂…а_1n

А= а₂₁ а₂₂…а_2n - матрица системы

а_m1 а_m2…а_mn

Решение системы – набор чисел k₁, k₂, k_n, если при подстановки их вместо неизвестных, каждое ур-ие системы становится тождеством.

Виды СЛУ:

-совместная (если имеет решение). М.б.: определенная (одно решение) и неопределенная (имеет бесконечно много решений);

-несовместная (если не имеет решений).

Этапы решения СЛУ:

1. Выяснить, является ли СЛУ совместной;

2. Если совместна, то определить её вид;

3. Найти метод её решения.

Вопрос 2.Методы решение систем линейных уравнений.

Формулы Крамера.

Теорема Крамера. Если определитель системы n линейных уравнений с n неизвестными отличен от нуля, то система имеет единственное решение, причём каждое неизвестное равно дроби, знаменателем которой служит определитель системы, а числителем, определитель, получаемый из знаменателя заменой столбца коэффициентов при определяемом неизвестном столбцом свободных членов.

2x+3y-z=5,

x+y+2z=7,

2x-y+z=1.

=18. _x=8, _y=38, _z= 40.

Замечание: 1. Если <>0, то система имеет единственное решение;

2. Если =0, то при _x=_y=_z=0, то система имеет бесконечное множество решений (неопределённая), а при _x<>0 или _y<>0 или <>0, то система не имеет решений (несовместна);

Метод Гаусса исключения неизвестных.

«Исключение неизвестных» означает построение равносильной системы линейных уравнений, имеющей ступенчатый вид, т.е. x₁ может содержаться не более, чем в одном уравнении, х₂ – не более чем в двух и т.д.

Пример 1. Пример 2.

x₁ + 2х₂ + 3х₃ – 2х₄ = 6, x₁ + 2х₂ + 3х₃ – 2х₄ = 6,

2x₁ – х₂ – 2х₃ – 3х₄ = 8, 2x₁ – х₂ – 2х₃ – 3х₄ = 8,

3x₁ + 2х₂ – х₃ + 2х₄ = 4, 3x₁ + 2х₂ – х₃ + 2х₄ = 4,

2x₁ – 3х₂ + 2х₃ + х₄ = – 8. 5x₁ + х₂ – 3х₃ – х₄ = 14.

Ответ: (1, 2, –1, 2). Ответ: (23 – 10,8х₄, –4 – 3,4х₄, 2х₄+ 3, х₄).

Матричная запись системы линейных уравнений.

Рассмотрим снова систему уравнений, имеющую основную матрицу А.

Используя правило умножения матриц, систему можно записать в эквивалентном матричном виде:

(*) АХ = Н

Пусть определитель  матрицы А отличен от нуля. Тогда, система имеет единственное решение, которое находится по формулам Крамера.

Дадим теперь другую форму записи решения матричного уравнения (*). Для этого введем понятие обратной матрицы.

Обратной для матрицы А называется такая матрица (обозначе­ние А^-1), которая удовлетворяет условиям

А^-1А=АА^-1= Е,

где Е — единичная матрица.

Если определитель   0, то обратной для мат­рицы А является следующая матрица:

А^-1 = ,

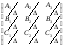где, как и ранее, А_i, В_i, С_i – алгебраические дополнения соответ­ственно элементов a_i, b_i, c_i ( i = 1, 2, 3).

Матрицы А и А^-1 назы­ваются взаимнообратными.

Замечание. Если определитель матрицы А равен нулю ( = 0), то обратная матрица не существует.

Воспользуемся обратной матрицей для решения уравнения (*). Умножая уравнение слева на матрицу А^-1, получаем

А^-1АХ = А^-1Н

Так как А^-1А = Е, а ЕХ = X, то X = А^-1Н.

Теорема Кронекера-Капелли

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Теорема Кронекера-Капелли применяется при исследованиях систем алгебраических уравнений (без непосредственного решения системы). В результате исследования должна быть записана эквивалентная система алгебраических уравнений с минимальным числом уравнений.