2. Задача анализа детерминированной системы

Постановка задачи

Пусть исследуется производственный процесс, в котором поступление требований происходит через равные промежутки времени (т.е. интенсивность потока поступлений требований) и обслуживание производится через равные промежутки времени(т.е. интенсивность обслуживания). Имеется один канал обслуживания. Предполагается, что(в противном случае очередь будет бесконечно возрастать) и что к началу обслуживания в системе имеется ужеn требований. Определить, через какое время очередь исчезнет.

Выявление основных особенностей, взаимосвязей и количественных закономерностей

Величину называют коэффициентом использования СМО. Очередь будет бесконечно возрастать, если, а если же, то очередь будет иметь постоянную длину. Схематически работа рассматриваемой СМО представлена на рис. 12.2.

Рис. 12.2 Схема работы системы

Пока обслуживается очередь из n требований в течение времени , вновь поступит на обслуживаниетребований:

.

Аналогично, пока будут обслуживаться требований в течение времени, дополнительно поступит на обслуживаниетребований:

.

Это происходит до тех пор, пока , после чего очередь исчезнет.

Весь процесс функционирования СМО представим в аналитическом виде.

Построение математической модели

Время, через которое очередь исчезнет, можно представить в таком виде:

Исследование математической модели.

Для определения времени, через которое очередь исчезнет, необходимо раскрыть математическую модель.

В модели использована формула суммы геометрической прогрессии. Чем ближе интенсивность потока к интенсивности обслуживания, тем через больший промежуток времени исчезнет очередь (при). Членомможно для упрощения расчётов пренебречь, тогда.

3. Задачи анализа разомкнутой системы с ожиданием

4. (Потоки требований пуассоновские).

Постановка задачи

Пусть задана некоторая СМО, для которой справедливы следующие гипотезы:

1) Вероятность поступления требований не зависит от принятого начала отсчета времени, а зависит только от продолжительности периода наблюдений (стационарность потока);

2) Не поступают в систему и не покидают ее одновременно два или более требований (поток ординарный).

3) Поступление одного требования не зависит от поступления другого (отсутствие последействия).

Известны также интенсивность поступления потока требований (среднее число поступлений требований в единицу времени) и интенсивностьобслуживания требований (среднее число обслуживаний в единицу времени).

Требуется определить основные характеристики системы:

• вероятность простоя канала обслуживания ;

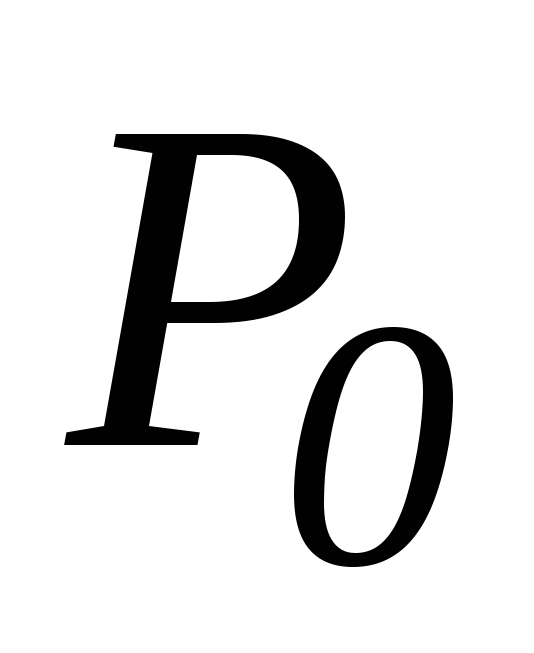• вероятность того, что в системе находится 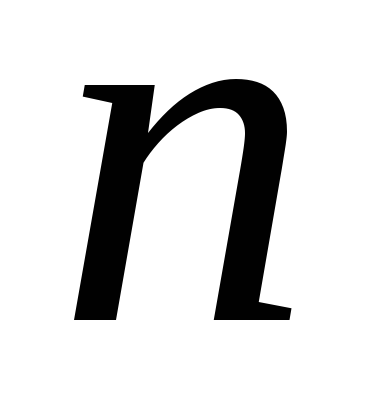требований;

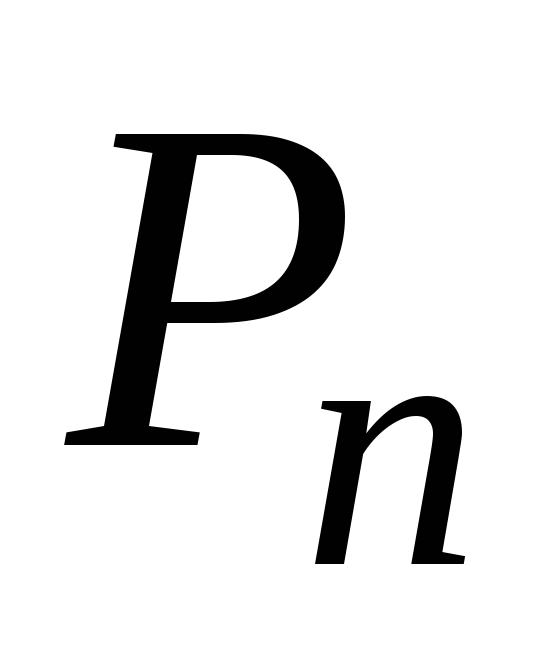• среднее число требований, находящихся в системе, 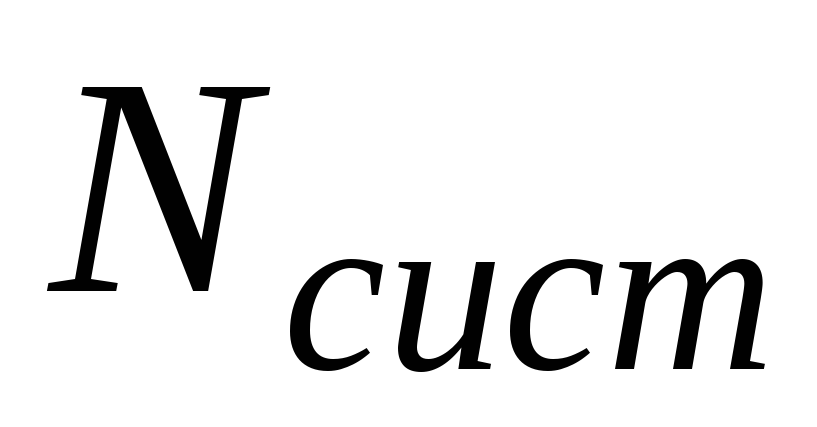(в очереди и на обслуживании);

• среднее число требований, находящихся в очереди, ;

• среднее время ожидания требования в системе .

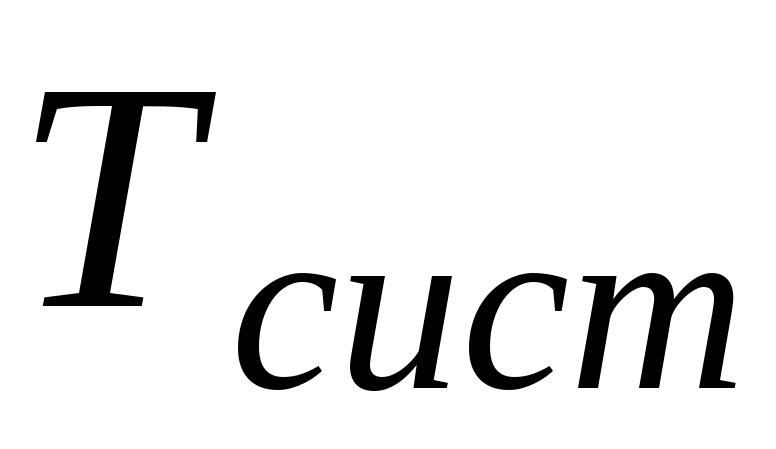Выявление основных особенностей, взаимосвязей и количественных закономерностей

Поток требований, обладающий свойством стационарности и отсутствием последействия, называется простейшим. В нашей задаче поток требований простейший. Основным понятием при анализе процесса СМО является состояние системы. Зная состояние системы, можно предсказать в вероятностном смысле её поведение.

Простейший поток – это стационарный пуассоновский поток. Если все потоки событий, переводящие систему из одного состояния в другое, являются пуассоновскими, то для этих систем вероятности состояний описываются с помощью системы обыкновенных дифференциальных уравнений.

Существует определённый методический прием, намного облегчающий вывод дифференциальных уравнений для вероятностей состояний. Первоначально строится размеченный граф состояний с указанием возможных переходов – это облегчает исследование и делает его более наглядным.

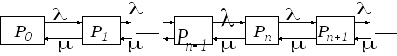
Рис. 12.3 Размеченный граф состояний одноканальной разомкнутой СМО с ожиданием

Граф состояний, на котором проставлены не только стрелки переходов, но и интенсивность соответствующих потоков событий, называют рамеченным.

Построение математической модели

Если составлен размеченный граф состояний, то для построения математической модели, т.е. для составления системы обыкновенных дифференциальных уравнений вероятностей состояний, рекомендуется использовать следующие кинематическое правило.

Производная вероятности пребывания системы в состоянииn равна алгебраической сумме нескольких членов:

• число членов этой суммы равно числу стрелок на графе состояний системы, соединяющих состояние n с другими состояниями;

• если стрелка направлена в состояние n, то член берётся со знаком плюс;

• если стрелка направлена из состояния n, то со знаком минус;

• каждый член суммы равен произведению вероятности того состояния, из которого направлена стрелка, на интенсивность потока событий, переводящего систему по данной стрелке.

В соответствии с размеченным графом состояний, используя мнемоническое правило, систему обыкновенных дифференциальных уравнений вероятностей состояний запишем так:

(уравнения Эрланга)

… ... …

Исследование математической модели

Ограничимся исследованием установившегося режима работы разомкнутой одноканальной системы.

Тогда .

Вместо системы обыкновенных дифференциальных уравнений получаем систему алгебраических уравнений:

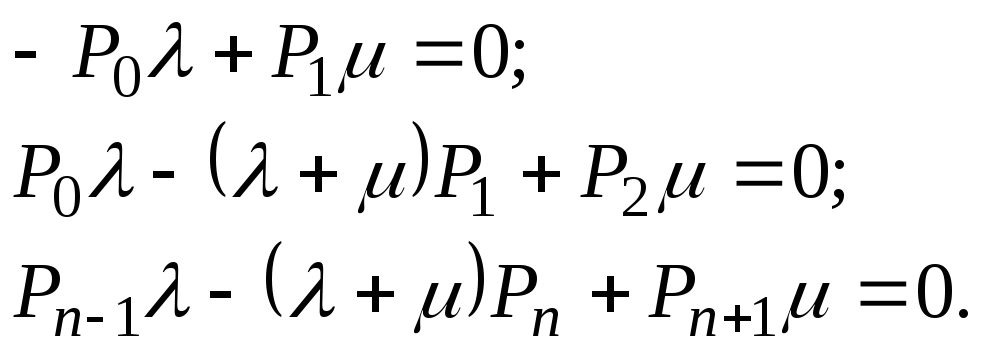
Используя полученную систему алгебраических уравнений, легко выразить вероятности состояний системы в виде некоторой рекуррентной формулы.

Из первого уравнения определяется вероятность наличия одного требования в системе

из второго уравнения – вероятность наличия двух требований в системе

.

Окончательно получим .

Аналогично проводятся преобразования для определения :

Окончательно получим и т. д.

Суммируя формулу сумму геометрической прогрессии, получаем

.

При отсюда имеем:

• вероятность простоя канала обслуживания ;

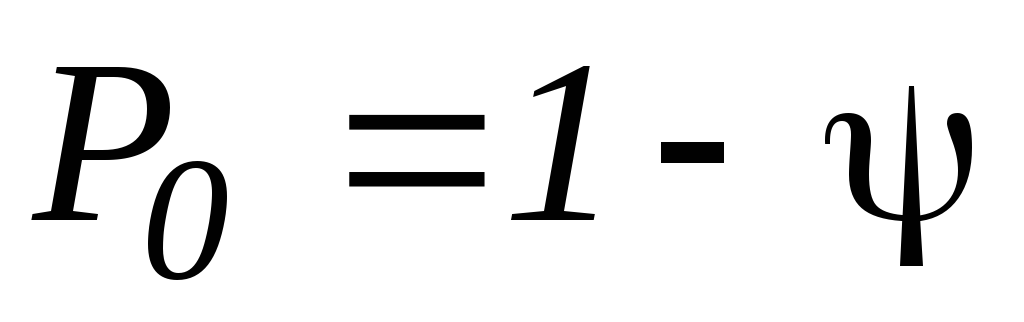• вероятность того, что в системе находится 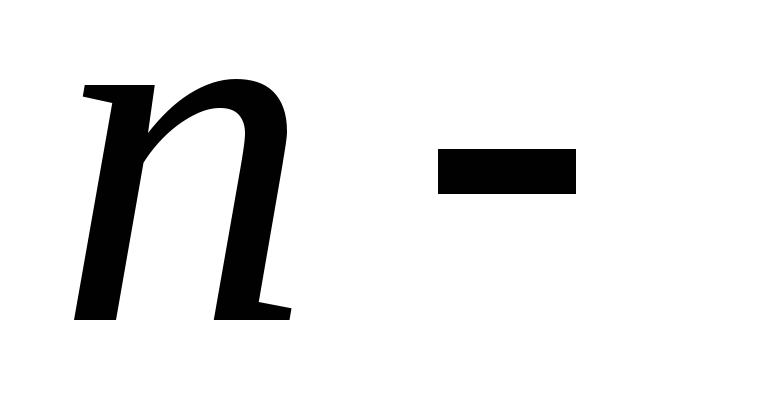требований

• среднее число требований, находящихся в системе (или математическое ожидание).

Последняя скобка является производной от следующего выражения:

,

т.е. равна .

Окончательно имеем

- среднее число требований, находящихся в очереди:

;

• среднее время ожидания требования в системе, которое можно определить, зная среднее число требований, находящихся в системе:

.