
- •Содержание
- •Структура и основные компоненты модели
- •Смысловое содержание учебно-методического материала.
- •Предлагаемая структура асоку
- •Метод дифференциальных уравнений
- •Алгоритм обучения с моделью обучаемого
- •Оптимизация: вероятностный анализ алгоритма обучения
- •Сходимость алгоритма обучения
- •5. Методология разработки обучающей программы, этапы проектирования, разработки и реализации обучающих программ на базе типовых элементов.
- •6. Элементы интерфейса обучающих программ.
- •6. Выводы
- •Используемая литература
Предлагаемая структура асоку
Основными вопросами при любой форме обучения являются следующие [9]:
· Какова цель обучения, чему необходимо научить студента?
· Как должна быть устроена система знаний для эффективного обучения?
· Какими общими свойствами она должна обладать независимо от предметной области и состава обучаемых?
· Как оценивать отдельные знания и как оценивать целостную систему знаний?
· Как правильно построить процесс обучения от исходных знаний к заключительным?
· Как обеспечить контроль за усвоением знаний?
· Как организовать управление учебным процессом? и т.д.
Предлагаемая концепция построения АСОКУ состоит в том, что если рассматривать проблему обучения, как часть более общей проблемы получения, структурирования, передачи и преобразования знаний, то следует применять научные методы, основанные на системном анализе и математическом моделировании.
Рассмотрим процесс обучения как процесс управления сложной системой [8], в которой обучаемый является объектом управления, а система обучения – источником управления.
Основополагающим звеном в АСОКУ является модуль МЗПО, в котором осуществляется конкретизация требований к формируемому уровню компетенции обучаемого. Структура МЗПО представлена на рис. 5.

Рис. 5. Структура модели знаний предметной области
МЗПО представляет собой базу данных параметризированных тестовых заданий, агрегированных с базой знаний предметной области. База знаний в ЭМЗ - это семантическая сеть, представленная ориентированным графом Gпо, вершинами которого являются концепты предметов, событий, состояний, а дуги создают отношения между ними. Данная семантическая сеть способна отобразить структуру знаний предметной области во всей сложности её взаимосвязей, увязать в единое целое объекты и их свойства. МЗПО строится на базе имеющихся печатных учебно-методических пособий, разработанных согласно требованиям «Типового учебного плана» конкретной специальности .
Каждой паре концептов в Gпо соответствует, как минимум одно тестовое задание из множества Q, где Q - вектор тестовых заданий для выполнения в процессе обучения. Q = {q1, q2, q3, …, qk}, где каждое qi = {С, R, L, F, t, b}. Здесь С – множество пар понятий (концептов) между которыми имеется семантическая связь R, причем множество R таково, что ; L- локаторы информационных ресурсов для поиска ответа на задание; F- режимы выполнения задания; t – временной норматив выполнения задания; b- уровень сложности требуемых знаний для выполнения задания.
Структура разработанной МСОУ аналогична структуре базы знаний ЭМЗ. Каждая связь между концептами в МЗОУ имеет весовые коэффициенты pij(th), т.е. вероятности того, что в h –й момент времени при диагностике знаний ОУ между i-м и j-м концептом будет обнаружена устойчивая семантическая связь. АСОКУ изменяет pij(th) в соответствии с результатами выполнения заданий Q = {q1, q2, q3, …, qk}. При этом учитываются многие параметры, такие как количество заданий в сеансе обучения, их информационная ёмкость (количество пар концептов, имеющих смысловую связь), количество повторений выполнения одного и того же задания, временные интервалы между повторениями, скорость усвоения информации, скорость забывания информации, степень сосредоточенности внимания обучаемого и др. Анализ структуры МЗОУ позволяет выявлять ошибочные семантические связи между концептами, имеющимися у обучаемого, этим самым вносить соответствующие коррективы в процесс обучения.
Представленная структура АСОКУ (рис. 4) частично реализована на базе веб-серверной технологии с использованием Apache, PHP, MySQL, Macromedia Flash MX.
Использование АСОКУ позволяет осуществлять различные формы обучения студентов. Также АСОКУ предназначена для исследования процессов восприятия человеком информации, её осмысления, запоминания, удержания в памяти с последующим воспроизведением.
Понятие обучающего оператора и его структура, операторное уравнение, база обучающей информации.
Все
математические операции над функцией
f
могут быть определены в терминах
операторов. Примером оператора является
дифференциальный оператор
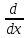 ;
выражение
;
выражение разбивается на оператор
разбивается на оператор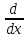 и подвергаемую воздействию оператора
функциюf.
Для функции
/ оператор
и подвергаемую воздействию оператора
функциюf.
Для функции
/ оператор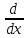 определяет
новую величину
определяет
новую величину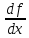 .
.
В
то время как f(x)
дает
значения величины функции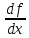 отх,
представляет
скорость изменения значения функции.
отх,
представляет
скорость изменения значения функции.
Другими обычными операторами являются logи sin. Два специальных оператора: единичный оператор, который оставляет всякую функцию без изменения, и нулевой оператор, который превращает любую функцию в нуль. В общем случае оператор О, примененный к величине х, определяет новую величинуОх. Следовательно, О представляет преобразование всех значений х. (Мы берем букву О, потому что это начальная буква слова оператор.)
Даже простые операции сложения и умножения могут быть определены в терминах операторов, и мы вводим здесь эти операторы. Оператор A, примененный к переменной х, означает прибавление постоянной а. (Символ А берется для обозначения сложения.)
Определение оператора А:
Ах = х + а. (1.2)
Обозначение Ах не означает «A, умноженное на х». Значение оператора А может стать яснее, если мы применим преобразование А к х более одного раза. Обозначение А2х будет употребляться для обозначения применения А к величине Ах. Тогда имеем определение:
А2х = А(Ах).
Мы видим из определения А, что применение А к некоторой величинех равносильно прибавлению к нему а. Следовательно, имеем
А (Ах) = (Ах) + а.
Но мы знаем из определения оператора А значение Ах и тогда получаем
А2х = А (Ах) = (Ах) + а = (х + а) + а = х +2а.
Мы можем обобщить это на случай п применений А к х и получим
Апх = ААА . . . Ах = х+па. (1.3)
Аналогично, оператор М, примененный кх, будет служить для обозначения того, что х должно быть умножено на достоянную m,
Определение оператора М:
Мх = тх. (1.4)
Заметим, что левая часть уравнения не означает«М, умноженное на х» (она означает «М применен к х»), но правая часть означает «т умножено на х».
Если применим М к х дважды, то получим
М2х = М (Мх) = т (Мх) = т • тх = m2х,
а если применим Мкх вобщем случае п раз, в результате будет
MnX=mnx (1.5)
Два оператора, Ж и А, определенные выше, играют большую роль в наших математических выводах, и мы здесь покажем, что будет, если применить оба оператора к х. Применим сначала Лі к а потом А кМх; в этомслучае получим
А (Мх) = (Мх) +а = тх + а.
Если теперь мы применим А кх, а потом М к Ах, то будем иметь
М (Ах) = т (Ах) = т(х-\-а) = тх +ma
Мы видим, таким образом, что важен порядок применений М и А.
Так как операція АМх дает другой результат, чем МАх, операторы M и A называются некоммутативными. Если порядок применения операторов может быть изменен без влияния на результат, пара операторов называется коммутативной.
Разность АМх — МАх = (тх+ а) - (тх + та) = a(1 —т)называетсякоммутаторомоператоров А и М.
Определение оператора L:
Lp=a+mp, 0≤р≤1. (1.6)
Переменная определена только для чисел от 0 до 1 включительно, так как не существует вероятностей' отрицательных и больших единицы.
Величина Lр рассматривается тоже как вероятность, так что и она определена тоже только от 0 до 1 включительно—требование, которое наложит ограничения на константыа ит. Наши основные операторы обучаемости будут аналогичныL из последнего равенства;р может быть вероятностью известной реакции при n-м испытании, Lр будет ее вероятностью при n+1 -м испытании. Оператор L в таком случае описывает действие следствия прип-м испытании на вероятностьр. Возникает вопрос, почему мы определяем операторL как линейное преобразование вероятности, а не какое-либо другое. Ответ прост: линейность предполагается с целью облегчить математическое исследование. Многие функции, используемые в работе, могут быть аппроксимированы полиномами. Чем выше степень полинома, тем лучше обычно аппроксимация. В самом деле, многие функции, такие, как синусы, логарифмы, экспоненты, могут быть представлены бесконечными рядами. С этой точки зрения предположение линейности, которое мы вводим, представляет собой использование первых двух членов ряда. Выражая это символически, если мы рассматриваем операциюОр как выражаемую рядом Оp = а0+a1р а2р2 . . . , то мы взяли Lр как аппроксимацию истинной функции Ор.
Использование линейного преобразования в представленной модели обучаемости может показаться многим читателям серьезным ограничением. Так оно и есть.
Однако скоро станет видно, что даже с этими простыми преобразованиями математика становится сложной и приводит ко многим неразрешимым проблемам в стохастических процессах. Надежда на разрешение их при помощи нелинейных преобразований тоже очень мала. Конечно, последнее оправдание предположения линейности зависит от соответствия между моделью и экспериментом, но если читателю это приятно, спешим заметить, что большая часть физикиосновывается на предположении линейности операторов. (Хотя линейные операторы являются основой развиваемого математического аппарата, линейность не является существенной для общего подхода.)
В последнем параграфе мы говорили о предположении «независимости от пути», согласно которому вероятность при n + 1-м испытании зависела от вероятности прип-м испытании, а не от пути ее получения, т. е. не зависела от более ранних значений вероятностей. Теперь мы видим желательность этого предположения, так как без негооперацияLрне былабы функцией от одного p, как это требует определение (равенство (1. 6)); она была бы функцией также и прошлых вероятностей. Можно упомянуть, что даже только операторы типа А могут быть использованы для построения модели обучаемости. Такую модель было бы в сущности легко применять. Но возникло бы одно весьма очевидное возражение, если бы операторы применялись прямо к вероятностям. Предположим, что а =0,1, а начальная вероятность реакции p = 0.1. Если происходит событие, делающее применимым А, вероятность реакции меняется нар+а=0, 1+0,1=0,2. Предположим, что после дальнейшего обучения вероятность достигла значения 0,9. Пусть опять наступает событие, делающее применимым A, и вероятность меняется на 0,1, достигая значения 1. Пример показывает, что приращение вероятности, благодаря каждому событию, равно 0,1 и при этом неважно, какой была вероятность. Этот результат противоречит нашему опыту, который внушает нам, что труднее уничтожить разницу между р = 0,9 и 1,0, чем между p = 0,1 и 0.2. Можно избежать этого противоречия, оперируя вместо самого р, с величиной, зависящей отр. К примеру, А можно применять к х, где х есть 1/(1—р).Тогда, еслиp = 0, x=1. Приа = 0,1 одно применение А ведет кАх =1,1, которое для новой величины р дает 0,091. Если p = 0,5, то х = 2, и применение А даетАх = 2.1. которое дает p = 0,524. Подобная постановка вопроса ведет к тем меньшему изменениюр, чем больше значение величины, зависящей отр. Замечания, подобные данным, могли быть сделаны и относительно оператора М. Говорить больше об этом мы здесь не будем. В действительности мы используем М в особых случаях.
