31.Степеневі ряди в комплексній площині. Теорема Абеля. Властивості степеневих рядів.

Степеневим рядом називається ряд вигляду ,

де комплексне число, комплексна змінна

Теорема Абеля:

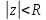Якщо ряд збігається при (в околі точки z0), то він збіжний при довільних z; .Якщо ж ряд розбіжний при, то розбіжний при довільнихz З теореми Абеля випливає, що існує така точкаR, що при довільних z ряд розбіжний, якщо, ряд збіжний.

Властивості степеневих рядів:

1.Сума степеневого ряду в області є аналітичною функцією.

2.Степеневий ряд в області його збіжності можна довільну кількість разів диференціювати та інтегрувати. При цьому отримаємоо ряд обл. збіж якого співпадає з обл. збіж вихідного ряду

32.Ряд Тейлора для функції комплексної змінної.

Теорема: Довільна аналітична в колі функції f(z) може бути єдиним чином представлена у вигляді степеневого ряду , де

Доведення:

Візьмемо довільну точку z в колі і проведемо коло радіусомr, яке не містить точку z і лежить і колі радіуса R Функціяf(z) аналітична в , тодіде ξ – точка на колі

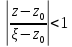, Отже, має місце розклад в рядПомножимо цей ряд наf(ξ)ОтримаємоПроінтегруємо, цю рівність по

33.Ряд Лорана.

Теорема: Довільна аналітична в кільці функт функц f(z) може бути розкладена в ряд Лорана. , L – довіл замкн контур, що цілком лежить в кільці

Доведення: Візьмемо довільну точку z в кільці, потім побудуємо 2 кола L1, L2 таких, що т.z лежить між цими кільцями і вони не перетинають вихідне кільце. Тоді за теоремою Коші для двозв’язної області маємо , деL1,L2 обхід проти годинникової стрілки. Аналогічно попередній теоремі Помножимо на

Інтеграл L2 де L1:

Помножимо на

Інтегруємо по L1:

34.Нулі аналітичної функції.

Нехай функція f(z) аналітична в області Д, точка .Означення: Точка назив нулем функціїf(z) порядку m , якщо =З цього означення, що якщо z0 – нуль m-го порядку, то розклад функції f(z) в ряд Тейлора буде мати вигляд

Теорема: Для того, щоб m-ка z0 була нулем порядку m для функції f(z) необхідно і дост , щоб f(z) мала вигляд аналітична в Д і

Доведення: Нехай точка z0 – порядку m для f(z), тоді

f(z)=

=

Нехай

Розкладемо є нулем порядку m для f(z).

35.Ізольовані особливі точки і їх класифікація.

Точки в яких порушується умова аналітичності функції f(z) назив особливими. Ізольованою особлив точкою назив точка в околі якої немає інших особл точок функт f(z). Означення: ізольовану особливу точку z0 однозначної аналітичної в околі точки z0 функції f(z)будемо називати: а) усувною особлив точкою,якщо існує скінченна границя функт f(z) при z, тобто існує б)полюсом порядку m, якщо в)істотно особливою точкою якщо не існує ні скінченна, ні нескінченна границя . Усувна особлива точка(Теорема) – точка z0 є усувною особливою точкою для f(z) коли розклад в ряд Лорана функції f(z) в околі точки не містить головної частини. 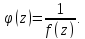Полюс (Теорема) – для того, щоб точка z0 була нулем функції Істотно особлива точка(Теорема) – для того, щоб точка z0 була істотно особлив, необхідно і дост,щоб головн част ряду Лорана містила нескінченну кількість членів