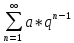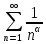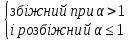- •1.Числові ряди. Основні властивості та дослідження ряду геометричної прогресії.
- •2.Основні властивості числових рядів.
- •3.Ознака порівняння та гранична ознака порівняння для знакододатних рядів.
- •4.Ознака д’Аламбера, радикальна ознака Коші.
- •5.Інтегральна ознака коші.
- •6.Ряди, в яких знаки членів строго чергуються. Ознака Лейбніца.
- •7.Знакозмінні ряди. Абсолютна і умовна збіжність.
- •Доказано.
- •8.Функціональні ряди. Поняття рівномірної збіжності. Ознака Вейерштрасса.
- •9.Степеневі ряди. Теорема Абеля. Інтервал та радіус збіжності степеневого ряду.
- •10.Властивості степеневих рядів.
- •11.Ряди Тейлора і Маклорена.
- •12.Наближені обчислення за допомогою степеневих рядів.
- •13.Ряди Фур’є. Гармонічні коливання.
- •16. Розклад в ряд Фур’є функцій довільного періоду. Представлення неперіодичної функції рядом Фур’є.
- •17.Комплексні числі і дії над ними.
- •18.Функції комплексної змінної. Основні поняття.
- •19.Границя і неперервність функції комплексної змінної.
- •20.Елементи функції комплексної змінної
- •22.Елементи функції комплексної змінної , і зв’язок між ними.
- •23. Диференціювання функцій комплексної змінної. Умови Коші-Рімана.
- •24.Аналітична функція. Диференціал.
- •25.Гармонічні функції.
- •26.Інтегрування функцій комплексної змінної. Основні властивості інтегралів від функцій комплексної змінної.
- •27.Основна теорема Коші і наслідки з неї.
- •28.Первісна і невизначений інтеграл від функції комплексної змінної. Формула Ньютона-Лейбніца.
- •29.Інтегральна формула Коші і наслідки з неї.
- •30.Числові ряди в комплексній площині. Необхідна умова збіжності та теорема про абсолютну збіжність таких рядів.
- •31.Степеневі ряди в комплексній площині. Теорема Абеля. Властивості степеневих рядів.
- •32.Ряд Тейлора для функції комплексної змінної.
- •33.Ряд Лорана.
- •34.Нулі аналітичної функції.
- •35.Ізольовані особливі точки і їх класифікація.
- •36.Нескінченно віддалена особлива точка.
- •37.Означення лишку. Теорема Коші про лишки.
- •38.Обчислення лишків.
- •39.Застосування лишків до обчислення дійсних визначених інтегралів.
- •40.Оригінали і їх зображення. Теореми про існування зображення та єдність оригіналу.
- •41.Властивості перетворення Лапласа: лінійність, подібність, зміщення.
- •47.Випадкові події. Класичне означення ймовірності. Властивості ймовірності.
- •48.Відносна частота. Означення статичної і геометричної ймовірностей.
- •49.Теорема додавання ймовірностей несумісних подій. Повна група подій. Протилежні події.
- •50.Умовна ймовірність. Теорема множення ймовірностей. Незалежність подій.
- •51.Теорема про ймовірність суми сумісних подій.
- •52.Формула повної ймовірності.
- •Доказано.
- •55.Оцінка найбільш ймовірного числа появи дискретної випадкової величини.
- •56.Теорема Пуассона.
- •57.Локальна та інтегрально теореми Муавра-Лапласса.
- •58.Математичне сподівання дискретної та неперервної випадкових величин та його властивості.
- •Доказано.
- •Доказано.
- •Доказано.
- •59.Дисперсія і середнє квадратичне відхилення.
- •60.Неперервні випадкові величини та функція ймовірності розподілу.
1.Числові ряди. Основні властивості та дослідження ряду геометричної прогресії.
О.1: Числовим рядом називається вираз вигляду:
∑∞n=1 Um = U1 + U2 + … + Um + …
(1.1)
Де U1, U2, … – дійсні бо комплексні числа.
Um – загальний член ряду.
Ряд 1.1 вважається заданим, якщо відомий член ряду.
Um = f(n)
О.2: Сума перших n членів ряду називається n-тою частинною сумою ряд у 1.1 і позначається
Sn = U1 + U2 + … + Un = ∑∞n=1 Un
О.3: Якщо існує скінченна границя послідовності частинних сум Sn, тобто

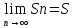
То ця границя називається сумою ряду 1.1. При цьому ряд 1.1 називається збіжним.
Якщо
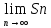 не існує або
не існує або ,
то ряд називається збіжним.
,
то ряд називається збіжним.
О.4: Геометричний ряд
a + aq + aq2 + aq3 + … + aqn-1 + …
(1.2)
Sn = a + aq + … + aqn-1
qSn = aq + aq2 + … aqn
Sn – qSn = a - qn
Sn
=


|q| < 1 => qn -> 0, n->
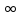 ;тоді
;тоді
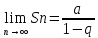 ,
отже
ряд збіжний і
,
отже
ряд збіжний і

|q| > 1 => qn -> ∞, n->
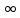 ;тоді
;тоді ,
розбіжний
,
розбіжний|q| = 1,
Нех q = 1, тоді ряд 1.2 набуде вигляду:
a + a + .. + a + …
ряд
розбіжний бо Sn=an,
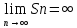
Нех q = -1;
a – a + a - … + a – a + … -
Ряд розбіжний.
Отже
ряд збіжний при |q|<1
і
його сума S
=
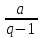
2.Основні властивості числових рядів.
Якщо ряд 1.1 збіжний і має суму S, то збігається також ряд
 C
= const,
і сума цього ряду буде cS
C
= const,
і сума цього ряду буде cS
Доказ: запишемо
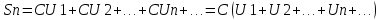
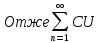
Нехай ряди ∑∞n=1 Un i ∑∞n=1 Vn збіжні і мають єдину s і S` відповідно. Тоді будуть збіжні ряди
 причому
їх суми будуть
причому
їх суми будуть

Доказ:
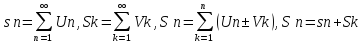
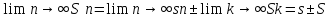
Якщо ряд 1.1 збігається, то збігається і ряд, утворений відкиданням довільного скінченного числа членів цього ряду.
Доказ:

Відкинемо всі члени після Uk.
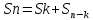 ,
де
,
де
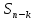 -
сума членів ряду, що містяться вSn,
але
не містяться в Sk.
-
сума членів ряду, що містяться вSn,
але
не містяться в Sk.
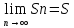
Sk
– число,

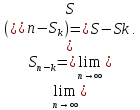
Отже ряд збіжний.
Наслідки: для того, щоб ряд 1.1 був збіжний (розбіжний) треба щоб був збіжний (розбіжний) довільний його залишок.
4.(Необхідні умови збіжності ряду).
Якщо ряд ∑∞n=1 Un збігається, то lim Un = 0
Доказ:
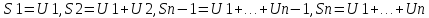
Sn-Sn-1 = Un
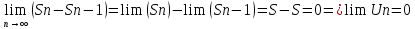
5.Достатня
умова розбіжності ряду. Якщо lim
Un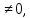 то
ряд розбігається.
то
ряд розбігається.
Доведення випливає з 4.
3.Ознака порівняння та гранична ознака порівняння для знакододатних рядів.
Теорема 1 (ознака порівняння)
Якщо маємо 2 ряди з невд'ємними членами
U1+U2+…+Un+... Un>=0 (3.1)
V1+V2+…+Vn+… Vn>=0 (3.2)
І
виконується
умова
Un>=Vn
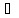 n>=1
n>=1
Тоді: з збіжності ряду Vn випливає збіжний ряд U ;
А з розбіжного ряду U випливає розбіжний V
Доказ: Запишемо частинні суми
Sn=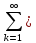 Uк
Sn=
Uк
Sn=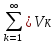
Нехай
(3.2) – збіжний випливає
 ;
;
Оскільки
Sn’
не спадна то
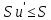 ;
;
А оскільки Sn<Sn’, то Sn<=Sv’<=S
Sn=
монотонна і не спадна , обмежена зверху
тже за теоремою про границю монотонної
обмеженої послідовності існує скінченна
границя Sn
Якщо
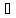
 то ряд 3.1 збіжний . (кінець доказа)
то ряд 3.1 збіжний . (кінець доказа)
Якщо 3.1 розбіжний то 3.2 також розбіжний , бо за вже доведення якщо 3.2 збіжний то 3.1 збіжний
Ряди що часто використовуються для для порівняння
В
умові теореми 1 умову , що Um<=Vm m>=1
можно замінить , що Um<=Vm
для
m>=1
можно замінить , що Um<=Vm
для
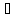 m>=N(за
3ю властивлстю)
m>=N(за
3ю властивлстю)
Теорема 2 : Граничга ознака порівняння
Нехай задано 2 ряди з додатніми числами:
U1+U2+Un+… Un>0 (3.3)
V1+V2+Vn+…Vn>0(3.4)
І
 скінченна
, відмінна
від
0 lim
скінченна
, відмінна
від
0 lim
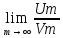 =a(
=a( 0,
0, ;=const);
;=const);
Тоді ряди вежуть себе однаково
Доказ:
нехай з умови, що
 скінченний за означенням
скінченний за означенням
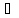 Є>0
Є>0
 N=N(Є)
N=N(Є)
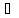 n>N
n>N
 <Є;
<Є;
-Є< -a<Є;
а-Є<
-a<Є;
а-Є<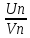 <Є+а
<Є+а
(а-Є)Vn<Un<Vn(a+Є); (3.5)
Виберимо Є так , щоб а – Е >0 , то б то Є<a;
Нехай (3.3) збіжний => з відношення 3.5 за теоремою 1 ряд Vn(c.) теж збігається => за властивісттю 1 ряд Vn збіжний
Нехай (3.3) розбіжний , тоді з 3.5 за теоремою 1 ряд V(Є+а) теж розбіжний , тоді з 3.5 за теоремою 1 ряд V(Є+а) теж розбігається і за властивістю 1 ряд V розбіжний