15. Конъюнкция. Дизъюнкция. Инверсия. Функционально полная система лф. Функции и-не, или-не, Исключающее или.

Конъю́нкция(от лат. conjunctio союз, связь) — логическая операция, по своему применению максимально приближённая к союзу "и". Синонимы: логи́ческое "И", логи́ческое умноже́ние, иногда просто "И".

Конъюнкция может быть бинарной операцией, то есть, иметь два операнда, тернарной операцией, т.е. иметь три операнда или n-арной операцией, т.е. иметь n операндов. Чаще всего встречаются следующие варианты инфиксной записи:

По аналогии с умножением в алгебре знак логического умножения может быть пропущен: ab

В булевой алгебре конъюнкция — это функция двух, трёх или более переменных (они же — операнды операции, они же — аргументы функции). Переменные могут принимать значения из множества {0,1} . Результат также принадлежит множеству {0,1}. Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений 0, 1 может использоваться любая другая пара подходящих символов, например false,trueилиF,Tили "ложь", "истина".

Правило: результат равен 1, если все операнды равны 1; во всех остальных случаях результат равен 0.

Таблицы истинности:

abab

0 0 0

0 1 0

1 0 0

1 1 1

Конъюнкция коммутативна, ассоциативна и дистрибутивна по отношению к слабой дизъюнкции.

Дизъю́нкция — (лат.disjunctio- разобщение) логическая операция, по своему применению максимально приближённая к союзу «или» в смысле «или то, или это, или оба сразу». Синонимы: логи́ческое «ИЛИ», включа́ющее «ИЛИ», логи́ческое сложе́ние, иногда просто «ИЛИ».

Дизъюнкция может быть бинарной операцией, то есть, иметь два операнда, тернарной операцией, то есть иметь три операнда или n-арной операцией, то есть иметьnоперандов.

Запись может быть префиксной — знак операции стоит перед операндами (польская запись), инфиксной — знак операции стоит между операндами или постфиксной — знак операции стоит после операндов. При числе операндов более 2-х префиксная и постфиксная записи экономичнее.

Чаще всего встречаются следующие варианты записи:

a||b,a|b,ab, a+b, a OR b

В булевой алгебре дизъюнкция — это функция двух, трёх или более переменных (они же — операнды операции, они же — аргументы функции).

Правило: результат равен 0, если все операнды равны 0; во всех остальных случаях результат равен 1.

Таблицы истинности:

abab

0 0 0

0 1 1

1 0 1

1 1 1

Инвертирование— битовая операция переводящая 0 в 1 и 1 в 0. Логическое НЕ.

Функционально полной системой булевых функций(ФПСБФ) называется совокупность таких булефых функций (f1,f2, ...fk), что произвольная булева функцияfможет быть записана в виде формулы через функции этой совокупности.

Исходя из определения СДНФ, СПНФ, СКНФ и ФПСБФ следует отнести системы: (/\, \/, не),(/\,, не). Это обуславливает целесообразность постановки задачи определения свойств, которыми должны обладать функции, составляющие ФПСБФ.

Решение этой задачи основано на понятии замкнутого относительно операции суперпозиции класса функций. Класс булевых функций, функционально замкнутый по операции суперпозиции, есть множество функций, любая суперпозиция которых дает функцию, также принадлежащую этому множеству. Среди функционально замкнутых классов выделяют классы обычного типа, называемые предполными, которые обладают следующими свойствами. Предполный класс Sне совпадает с множеством Р2 всех возможных булевых функций, однако, если в него включить любую, не входящую вS, булеву функцию, то новый функционально замкнутый класс будет совпадать с множеством Р2. Проведенные исследования показали, что преднолных классов пять, а для построения ФПСБФ необходимо и достаточно, чтобы ее функции не содержались полностью ни в одном из пяти предполных классов.

Перечислим предполные классы булевых функций:

• булевы функции, сохраняющие константу 0;

• булевы функции, сохраняющие константу 1;

• самодвойственные булевы функции;

• линейные булевы функции;

• монотонные булевы функции;

К булевым функциям сохраняющим константу 0, относят такие булеы функцииf(x1,...,xn), для которых справедливо соотношениеf(0,...,0)=0.

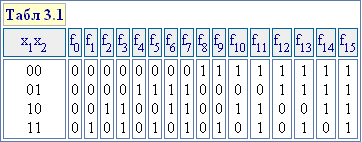
Примерами булевых функций, сохраняющих константу 0, являются функции f0,f1,...,f7 (табл 3.1). Поскольку таблица истинности для функций, сохраняющих константу 0, в первой строке значений функций содержит 0, то имеется ровно 22(^n)-1 таких функций.

К булевым функциям сохраняющим константу 1, относят такие булеы функцииf(x1,...,xn), для которых справедливо соотношениеf(1,...,1)=1.

Примерами булевых функций, сохраняющих константу 1, являются функции f1,f3,f5,f7,f9,f11,f13,f15 (табл 3.1). Поскольку таблица истинности для функций, сохраняющих константу 1, в последней строке значений функций содержит 1, то имеется ровно 22(^n)-1 таких функций.

Булевы функции f1(x1,...,xn) иf2(x1,...,xn) называютсядвойственнымидруг другу, если выполняется соотношениеf1(x1,...,xn)=/(f2(/x1,...,/xn))

Двойственными являются функции f0 иf15,f1 иf7,f2 иf11 и т.д. (табл 3.1).

К самодвойственнымбулевым функциям относят такие булеы функции, которые двойственны по отнощению к самим себе, т.е. справедливо соотношениеf(x1,...,xn)=/(f(/x1,...,/xn)). Если условия назвать противоположными наборами, набор <y1,y2,...,yn> и набор </y1,/y2,...,/yn>, то определение самодвойственных функций дадим следующее.

Булева функция называется самодвойственной, если на любых двух противоположных наборах она принимает противоположные значения.

Самодвойственными являются функции f3,f5,f10,f12 (табл 3.1). Из определения самодвойственной функции следует, что она полностью определяется своими значениями на первой половине строк таблицы истинности. Поэтому число всех самодвойственных булевых функцийf(x1,...,xn) равно

К линейным булевым функциямотносят такие булевы функции, которые представимы в виде

f(x1,...,xn)=с0 +c1x1 + ... +cnxn,

где ciE{0,1}, а + операция "сумма поmod2".

Линейными являются булевы функции f0,f3,f5,f6,f9,f10,f12,f15, (табл 3.1), ибо

f0 = 0, f3 = x1, f5 = x2, f6 = x1 + x2, f9 = x1 + x2 + 1, f10 = /x2 = 1 + x2, f12 = /x1 = 1 + x1, f15 = 1.

Поскольку линейная функция однозначно определяется заданием коэффициентов с0,...,сn, то число линейных функций равно 2^(n+1).

Двоичный набор Y= <y1,y2,...,yn> не меньше двоичного набораB= <b1,b2,...,bn> , если для каждой пары (Yi,Bi)i= 1...nсправедливо соотношениеYi>=Bi.

Так, набор 1011 >= 1010. Вместе с тем наборы 1011 и 0100 несравнимы в том смысле, что для них не выполняется ни соотношение Y>=B, ниY<=B.

Булева функция f(x1,...,xn) называетсямонотонной, если для любых двух наборовY= <y1,y2,...,yn> иB= <b1,b2,...,bn> таких, чтоY>=Bимеет место неравенствоf(y1,...,yn)>=f(b1,...,bn).

Монотонными являются булевы функции f0,f1,f3,f5,f7,f15 (табл. 3.1). Вместе с тем функцияf2 из табл. 3.1 не является монотонной, так какf2(1,0) >f2(1,1), хотя набор <1,0> меньше, чем набор <1,1>.