- •Электронный учебник по курсу "Основы оптики"
- •1. Описание световых волн
- •1.1. Основные свойства световых полей
- •1.2. Уравнения Максвелла
- •1.3. Математическое описание электромагнитных волн
- •1.3.1. Волновые уравнения
- •1.3.2. Монохроматическое поле
- •1.3.3. Комплексная амплитуда
- •Сложение некогерентных полей
- •1.4.3. Квазимонохроматическое и полихроматическое поле
- •1.4.4. Простейшие монохроматические волны
- •Плоские и сферические волны
- •2. Энергетика световых волн
- •2.1.3. Сила излучения
- •2.1.4. Энергетическая яркость
- •2.1.5. Инвариант яркости вдоль луча
- •2.1.6. Поглощение света средой
- •2.2. Световые величины
- •2.2.1. Световые величины
- •2.2.2. Связь световых и энергетических величин
- •Сопоставление энергетических и световых единиц
- •2.4. Поток от излучателей различной формы
- •2.5. Яркость рассеивающей поверхности
- •2.6. Освещенность, создаваемая различными источниками (закон обратных квадратов)
- •3 Прохождение света через границу раздела двух сред
- •3.1. Отражение и преломление света на границе раздела двух сред
- •3.1.1. Закон преломления
- •3.1.2. Закон отражения
- •3.3.3. Просветление оптики. Тонкие пленки
- •4. Геометрическая оптика
- •4.1. Приближение коротких длин волн. Уравнение эйконала
- •4.2. Основные понятия геометрической оптики
- •4.2.1. Волновой фронт и лучи
- •4.2.2. Оптическая длина луча
- •4.2.3. Конгруэнция лучей.
- •4.2. Основные понятия геометрической оптики
- •4.2.1. Волновой фронт и лучи
- •4.2.2. Оптическая длина луча
- •4.2.3. Конгруэнция лучей.
- •4.4. Пучки лучей
- •4.4.1. Гомоцентрические пучки лучей
- •4.4.2. Негомоцентрические пучки
- •4.4.3. Астигматический пучок
- •4.5. Перенос поля в приближении геометрической оптики. Пределы применимости геометрической оптики
- •4.5.1. Уравнение переноса комплексной амплитуды в приближении геометрической оптики
- •4.5.2. Пределы применимости геометрической оптики
- •5. Геометрическая теория оптических изображений. Идеальные оптические системы
- •5.1. Описание оптических систем
- •5.1.1. Элементы оптических систем
- •Оптические среды
- •Оптические поверхности
- •Диафрагмы
- •5.1.2. Взаимное расположение элементов в оптической системе Центрированная оптическая система
- •Правила знаков
- •Меридиональная и сагиттальная плоскости
- •5.2.2. Линейное, угловое, продольное увеличение
- •5.2.4. Построение изображений
- •5.3. Основные соотношения параксиальной оптики
- •5.3.1. Зависимость между положением и размером предмета и изображения
- •5.3.2. Угловое увеличение и узловые точки
- •5.3.3. Частные случаи положения предмета и изображения
- •5.3.4. Связь продольного увеличения с поперечным и угловым
- •5.3.5. Диоптрийное исчисление
- •5.3.6. Инвариант Лагранжа-Гельмгольца
- •6. Матричная теория Гауссовой оптики
- •6.3.1. Пакет из плоскопараллельных слоев
- •7. Реальные оптические системы. Ограничения пучков
- •7.1. Реальные (действительные) лучи
- •7.1.1. Расчет хода реальных лучей
- •7.1.2. Причины «непрохождения» лучей через поверхность
- •7.2. Ограничения пучков лучей
- •7.2.1. Апертурная диафрагма
- •7.2.2. Полевая диафрагма
- •7.2.3. Виньетирование
- •7.3. Описание предметов, изображений и зрачков
- •7.3.1. Обобщенные характеристики
- •7.3.2. Обобщенный инвариант Лагранжа-Гельмгольца
- •8.1.3. Волновая аберрация
- •8.1.4. Продольные аберрации
- •8.2. Монохроматические аберрации
- •8.2.3. Кома
- •Кома и неизопланатизм
- •8.2.4. Астигматизм и кривизна изображения
- •8.2.5. Дисторсия
- •8.3. Хроматические аберрации
- •8.3.1. Хроматизм положения
- •Принципы ахроматизации оптических систем
- •8.3.2. Хроматизм увеличения
- •9. Структура и качество оптического изображения
- •9.1.4. Оптическая передаточная функция (опф)
- •9.2. Схема формирования оптического изображения
- •9.3. Дифракционная структура изображения
- •9.3.1. Функция рассеяния точки в случае отсутствия аберраций
- •Фрт безаберрационной оптической системы
- •9.3.2. Влияние неравномерности пропускания по зрачку на фрт
- •9.3.3. Безаберационная опф. Предельная пространственная частота
- •9.4. Критерии качества оптического изображения
- •9.4.1. Предельная разрешающая способность по Релею
- •9.4.2. Разрешающая способность по Фуко
- •9.5. Влияние аберраций на фрт и опф
- •9.5.1. Число Штреля
- •9.5.2. Критерий Релея для малых аберраций
- •9.5.3. Формула Марешаля. Допуск Марешаля для малых аберраций
- •9.5.4. Влияние аберраций на опф. Геометрически-ограниченные и дифракционно-ограниченные оптические системы
- •Глоссарий абвгдезиклмнопрстуфхцчэя a
8.2. Монохроматические аберрации
Аберрации делятся на монохроматическиеихроматические. Монохроматические аберрации присутствуют, даже если оптическая система работает примонохроматическом излучении.
8.2.1. Разложение волновой аберрации в ряд
Для описания отдельных типов аберраций
волновую
аберрациюможно разложить в
ряд по степенямканонических
зрачковых координат: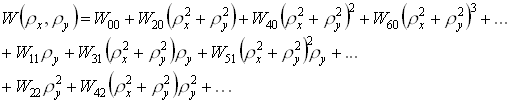
или в полярных координатах:
|
где
![]() (
(![]() – степень
– степень![]() ,
,![]() –
степень
–
степень![]() )
– коэффициент, значение которого
определяет вклад конкретного типа (и
порядка) аберрации в общую волновую
аберрацию.
)
– коэффициент, значение которого
определяет вклад конкретного типа (и
порядка) аберрации в общую волновую
аберрацию.
Порядок аберрации определяется по
степени координаты
![]() в
разложениипоперечной
аберрациив ряд:
в
разложениипоперечной
аберрациив ряд:
Разложение в ряд продольной
аберрацииимеет вид: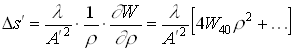
8.2.2. Радиально симметричные аберрации (дефокусировка и сферическая аберрация)
Радиально симметричные аберрации
(расфокусировка и сферическая аберрация)
анализируются и изучаются при рассмотрении
осевой точки предмета. Для описания
радиально симметричных аберраций
достаточно использовать одну радиальную
зрачковую координату
![]() :
:![]()
Дефокусировка
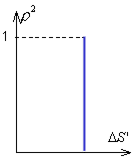
Дефокусировка не приводит к нарушению гомоцентричности пучка, а только свидетельствует о продольном смещенииплоскости изображения. В случае дефокусировки продольная аберрация постоянна для всех лучей пучка.
|
волновая аберрация |
продольная аберрация |
поперечная аберрация | |
|
|
| |
|
|
|
|
Сферическая аберрация 3 порядка
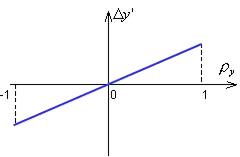
Сферическая аберрация приводит к тому, что лучи, выходящие из осевой точки предмета, не пересекаются в одной точке, образуя на плоскости идеального изображениякружок рассеяния. Ею обладают все линзы со сферическими поверхностями.
|
волновая аберрация |
продольная аберрация |
поперечная аберрация | |
|
|
| |
|
|
|
|
Сферическая аберрация 5 порядка
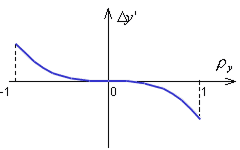
По характеру искажения гомоцентричности пучка лучей сферическая аберрация 5 порядка полностью аналогична сферической аберрации 3 порядка, только имеет более высокий порядок кривых на графиках поперечнойипродольнойаберраций.
|
Сочетая сферическую аберрацию и дефокусировку, можно выбрать наилучшее с точки зрения минимума сферической аберрации положение изображения. В частности, для сферической аберрации 3 порядка продольное смещение изображения, при котором кружок рассеяния минимален, составляет 2/3 от продольной аберрацииапертурного луча.
8.2.3. Кома
Кома появляется при смещениях точки
предмета с оси. Поперечная
аберрацияпри наличии комы
прямо пропорциональна величине предмета:![]() где
где![]() –
коэффициент пропорциональности,
определяющий качество аберрационной
коррекции оптической системы.
–
коэффициент пропорциональности,
определяющий качество аберрационной
коррекции оптической системы.
Волновая аберрация при наличии комы 3 и 5 порядков:
|
|
Поперечные аберрации при коме 3 порядка |
| |
|
|
| |
|
меридиональное сечение |
сагиттальное сечение |
точечная диаграмма |
|
|
|
|
|
|
| |