Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

МИРЭА - Российский технологический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

матан ( шпора )

.pdf

Скачиваний:

Добавлен:

10.05.2015

Размер:

2.7 Mб

Скачать

☆

1 / 21 2 > Следующая >>>

§1. Множество действительных чисел и его свойства.

A,B,C - множества.- пустое множество.

a,b,c - элементы множества. a A - принадлежность.

N Z Q R - вхождение одного множества в другое.

	p
r		, p Z,q N
r	q	, p Z,q N
	q

- "для любого" a N a 0

- "существует, найдется" ! - единственность

!1 N

- "или" a b

- "и"

- "если, то"

- "эквиваленция","необходимо и достаточно"

Свойства действительных чисел :

I (аксиомы сложения)

Опр.1 a,b R !a b - сумма элементов a и b. Операция нахождения суммы называется сложением.

1.a,b R a b b a - коммутативность

2.a,b,c R (a b) c a (b c) - ассоциативность

3.0 R a R a 0 0

4.a 0 R ( a) a ( a) 0

Сл.1 0 R - единственный

. 0 R 0 R

I3 I1 I3

0 0 0 0 0 0 !0 R .

II. (аксиомы умножения)

Опр.2 a,b R !a b - произведение элементов a и b. Операция нахождения произведения - умножение.

1.a,b R a b b a - коммутативность

2.a,b,c R (a b) c a (b c) - ассоциативность

3.1 0 R a R a 1 a. Сл. !1 R

4.a 0 1a - обратный для a - a 1a 1

III. (связь сложения и умножения)

1.a,b R (a b) c a c b c - дистрибутивность IV.(аксиомы порядка)

Опр.3 a R (a 0) (a 0) (a 0)

Если a 0, то ( a) 0

1.(a 0) (b 0) a b 0 2. (a 0) (b 0) a b 0

Опр.4 a,b R a b a b 0

V. (аксиомы непрерывности)

Опр.5 Отрезком a,b с концами A,B на множестве R

называют мн-во точек, удовлетв. условию a c b
(интервал (a,b), полуинтервал (a,b )
Опр.6 Система отрезков an ,bn ,n 1,2,3... называется
вложенной, т.е a1,b1 a2 ,b2 ... an ,bn , если:
a1 a2 ... an ... ... bn ... b2 b1
1. Система вложенных отрезков мн-ва R имеет точку,
общую всем этим отрезкам.
Опр.7 Система отрезков an ,bn - стягивающаяся, т.е
величина (bn an ) 0, если 0 n n n bn an
Т. Кантера (о непрерывности мн-ва R). Вложенная

система стягивающихся отрезков мн-ва R имеет общую, единственную точку для всех этих отрезков.

. I1 c an ,bn ,n 1,2,... Пусть d c, d an ,bn ,d c

d c 0, n n n bn an , d c bn an , d c d c 0, d c c - единственный .

Опр.8 R, элементы которого удовлетворяют аксиомам

I V групп называется мн-вом действ. чисел, а элементы этого множества - действ. числами.

Опр.9 Иррациональным числов называется действ. число, которое не является рациональным. Обозн: T.

Q T R, Q T , R R { , } ( , )a R a , a R a , .

§2. Модуль действ. числа и его свойства.

Опр.1 Модулем a R ( a ) называется наибольшее a и a

(1)

max{a, a}

(2)

a, если a 0

если a 0

(3)

- расстояние от начала координат до точки изобр.

число. a

Св.1

a b

. a

(a b)

a b

Св.2 Если a 0, b 0

или a 0,

b 0

ab. Если

a 0,b 0 или a 0,

b 0

ab.

Св.3 a b a b a b .

св.1

. a b a ( b) a b a b .

Св.4 a c (c 0) c a c

. a 0 a c, a 0 a c,a c a c a c.

§3. Функция (отображение). Действительные функции. Действительные переменные и их простейшие свойства.

Опр.1 Если каждому элементу x из мн-ва X ставится в соответствие по некоторому правилу и закону f !y Y y f (x), то говорят что на множестве X определена ф-ия

y f (x) или задано отображение f		: X Y.
y - образ элемента x (x - прообраз). X D(y)						- ООФ.
Способы задания функций:
1. алгебраический(аналитический): y 1				x	.
1. алгебраический(аналитический): y 1				x	.

sin x, если x 0
	2x 1, если 0					x 1
2. кусочно-аналитический: y	2x 1, если 0					x 1
	1		, если 1 x
	1		, если 1 x
	x 1

3. графический (нарисовать график, напр. y x ) Опр.2 f : X Y называется инъективным, если разным значениям x X соответствуют разные y Y.

Опр.3 f : X Y называют сюрьективным, если

y Y x y f (x).

Опр.4 f : X Y называется биективным, если оно одновременно инъективно и сюрьективно.

Опр.5 Если f : X Y и g :Y Z, то g f : X Z - композиция отображений или сложная функция. Опр.6 Если f : X Y - биекция, то f 1 :Y X - обратное отображение или обратная функция. Причем f 1 f 1 ( f f 1 1)

Опр.7 Действительной функцией действ. переменного x называется отображение из некоторого подмн-ва мн-ва действ. чисел в некоторое другое мн-во этого подмн-ва.

X D( f ), f : R X Y R, y f (x)

Опр.8 y f (x) монотонно возрастает(убывает) в своей области определения, если

x1,x2 D(y) x1 x2 f (x1 ) f (x2 ) f (x1 ) f (x2 )

Опр.9 Числовое мн-во X - симметрично относительно

O, если x X ( x) X.

Опр.10 y f (x) определенная на сим. мн-ве X - четная

(нечетная), если: f ( x) f (x) (f ( x) f (x))

Т.1 Сумма двух четных функций - функция четная, сумма четной и нечетной функций - функция нечетная.

. Пусть f (x), g(x) - четные ф-ии. Рассмотрим f (x) g(x). Т.к. f ( x) f (x) и g( x) g(x), то складывая равенства получим f ( x) g( x) f (x) g(x).

Т.е. f (x) g(x) - четная .

Т.2 Произведение двух четных и двух нечетных функций - функция четная, произведение четной и нечетной - - функция нечетная. (Доказывается аналогично) Опр.11. X называется ограниченным мн-вом если есть отрезок полностью содержащий это множество.

Опр.12 y f (x) - ограниченная, если ее Y - огр. мн-во.

§4. Числовые последовательности. Предел числовой числовой последовательности. Число е.

Опр.1 Отображение f : N R называется числовой последовательностью(ЧП). n xn (xn - общий член ЧП) ЧП ограничена снизу x1.

Опр.2 ЧП xn называется монотонно убывающей (возрастающей), если n N xn xn 1 xn xn 1 . Опр.3 Окрестностью точки a радиуса r 0 на числовой прямой наз-ся интервал с центром в этой точке. Обозн:

U(a,r) (a r,a r). Проколотая окр-ть: U(a,r)

(a r,a) (a,a r).

Опр.4 a lim xn : 0 N( ) n N xn a .

Опр.5 Последовательность, имеющая предел наз-ся сходящаяся.

Сходящиеся числовые последовательности обладают свойствами:

Т.1 Если последовательность сходится, то она имеет только один предел.

Т.2 Всякая сходящаяся последовательность ограничена.

Последовательность xn 1					1n n - сходится и
x		1	n	n
				e (число Бернулли).
lim	1

x x0

§5. Предел функции в точке. Свойства функций, имеющих предел в точке. Предел на бесконечности. Бесконечные пределы.

Пусть задана f (x) и x U(x0 ,r)

Опр.1 Число A наз-ся пределом функции в т. x0 , если:

0 ( ) 0 x U(x0 , ) f (x) A .

U(x0 , ) 0 x x0 .

Т.1 Если f (x) имеем предел в точке, то он единственный.

.		lim	f (x) A	lim		f (x) B		B A									B A	0
	x x0			x x0							B A				2

1 ( ) 0 x U(x0 , 1)							f (x) A							и
1 ( ) 0 x U(x0 , 1)							f (x) A							и
										2
												B A
	2	( ) 0 x U (x ,			2	)	f (x) B					B A		.
	2			0	2					2
							A B			2			A B
min{ 1, 2},x U(x0						, ),	A B		f (x)				A B			.
min{ 1, 2},x U(x0						, ),			f (x)							.
						2		2

Получили противоречие .

Т.2 Если ф-ия f (x) имеет предел в точке x0 , то f (x) -

- ограничена в некоторой проколотой окрестности этой точки.


. Пусть lim			f (x) A. Тогда 1 ( ) 0 x U(x0 , )
	x x0
	f (x) A	1

A 1 f (x) A 1 - f (x) - огр. в U (x0 , ) .

Т.3 Если lim			f (x) A, A 0,	то существуетU(x0 , ), где
	x x0

ф-ия сохраняет знак своего предела.

			тогда A
	. Пусть A 0,		тогда A		0	( ) 0 x U(x0 , )
				2
	f (x) A	A	f (x) A A			A		0.
		2			2		2
	Пусть A 0, тогда A
	Пусть A 0, тогда A				0 ( ) 0 x U(x0 , )
				2
	f (x) A	A	2	f (x) A A		2	A	2	0 .
	f (x) A	A		f (x) A A			A		0 .

Т.4 Если y f (x) имеет lim					f (x) y0 , а z g(y) -
				x x0		lim g( f (x)) z0 .
	lim g(y) z0 , то для z g( f (x))					lim g( f (x)) z0 .
	y y0					x x0

Опр.2 Число A называется пределом на бесконечности,

если lim f (x) A : 0 M ( ) 0 x x M

f (x) A .

Опр.3 Предел lim f (x) наз-ся бесконечным, если

x x0

M 0 (M ) 0 x U(x0 , ) f (x) M.

Опр.4 Бесконечный предел на бесконечности: ээ....

уу...аааа...на лекциях не давали.

§6. Бесконечно малые в точке функции и их свойства. Необходимые и достаточные условия существования

Опр. (x) - бесконечно малая (б.м.) ф-ия в точке x0 , если:

lim (x) 0: 0 ( ) 0	x U(x0 , )	(x)	.
x x0	ф-ий - ф-ия б.м. в точке x0.
Т.1 Сумма двух б.м. в точке x0	ф-ий - ф-ия б.м. в точке x0.

(методом матем. индукции теорема распространяется на

любое конечное число слагаемых).

. Пусть

x x

x x0

, тогда пусть

lim (x) 0

( ) 0 x U(x , )

(x)

2 ( ) 0 x U(x0

, 2 )

(x)

min{ 1, 2} x U(x0 , )

(x) (x)

(x)

lim (x)

(x) 0 .

x x0

Т.2 Произведение функции б.м. на функцию ограниченную

в точке x0 - функция б.м. в точке x0 .

. Пусть (x) - б.м. в точке x0 функция, а f (x) - огран.

Тогда для f (x) : M 0 x U(x0 , 1) f (x) M , а для


(x) : 0 2	( ) 0 x U (x0	, 2 )	(x)		,
				M

min{ 1, 2}, x U(x0 , ). Пусть g(x) (x) f (x), тогда

g(x)	(x) f (x)	(x)	f (x)	M	M
g(x) - б.м. в точке x0 .				M
g(x) - б.м. в точке x0 .

Т.3 Произведение любого числа б.м. функций в точке x0 - функция б.м. в этой точке.

Т.4 (критерий существования предела функции в точке)

lim				, где
lim	f (x) A	x U (x0	, ) f (x) A (x)	, где
x x0

(x) - б.м функция.

. 1.(необходимость)

Пусть lim f (x) A : 0 ( ) 0 x U(x0 , )

x x0

f (x) A , (x) f (x) A, f (x) A (x),

lim (x) 0.

x x0

2.(достаточность)

Пусть x U(x0 , ) f (x) A (x) lim (x) 0,

(x)	, (x) f (x) A,	f (x) A	lim	f (x) A.
.			x x0
.

§7. Арифметические операции над пределами.

Утв.1 Если f (x) C,	то	lim f (x) C.
Т.1 Если f (x) имеет lim		x x0			lim g(x) B, то
Т.1 Если f (x) имеет lim		f (x) A, а g(x) -			lim g(x) B, то
	x x0				x x0
lim( f (x) g(x)) A B.
x x0

. Т.к. lim f (x) A,	то x U(x0 , 1)			f (x) A (x),
x x0
lim (x) 0.
x x0

Т.к. lim g(x) B, то x U(x0 , 2 )			g(x) B (x),
x x0

lim b(x) 0. min{ 1, 2} x U (x0 , )					f (x) g(x)
x x0				lim (x) 0
A B (x), где (x) (x) (x),				lim (x) 0
lim f (x) g(x) A B .				x x0
lim f (x) g(x) A B .
x x0
Т.2 Если	lim	f (x) A lim g(x) B
	x x0		x x0
lim f (x) g(x) A B			.
x x0

. f (x) A (x), g(x) B (x), f (x) g(x) (A f (x)) (B (x))

бесконечно малая

A B B (x) A (x) (x) (x) A B x), где

(x) - б.м. в т. x0. Т.е. lim f (x) g(x) A B .

Сл. Постоянную (С) можно выносить за знак предела: lim Cf (x) C lim f (x).

x x0

Т.3 Если

lim

f (x) A lim g(x) B B 0

x x0

lim

f (x)

x x0

g(x)

- ограничена в U(x0 , ),

g(x)

0 ( ) x U(x0 , )

g(x) B

g(x)

f (x)

- ограничена в U (x0 , ),

g(x)

g(x) B

(x)) B A (B (x))

g(x) B

бесконечно малая

(x) B (c) A . Следовательно, по критерию

g(x) B

lim

f (x)

x x0 g(x)

§8. Предельный переход в неравенствах.

Т.1 Если

lim

f (x) A lim g(x) B A B

, )

то U(x

x x0

где f (x) g(x).

. В силу непрерывности мн-ва R :

A C B.

C A 0, 1 ( ) 0 x U(x0 , 1)

f (x) A

C A

f (x) A C A, f (x) C,

B C 0, 2 ( ) 0 x U(x0 , 2 )

g(x) B

B C

g(x) B (B C), g(x) C,

min{ 1, 2}, x U (x0 , )

f (x) C g(x) .

f (x) g(x) (x)

Т.2 Если x U(x0 , )

lim

f (x) lim (x)

lim

f (x) lim g(x) lim (x)

x x0

. Пусть lim f (x) lim g(x). Тогда 0 1, 2 ,

x x0

min{ 1, 2},x U (x0 , ),

f (x) A

(x) A

A f (x) g(x) (x) A A g(x) A

lim g(x) A .

x x0

Т.3 (о предельном переходе в неравенствах)

Если lim f (x) A,	lim g(x) B, то:
x x0	x x0

1)если f (x) g(x), то A B, 2)если f (x) g(x), то A B, 3)если f (x) B, то A B, 4) если f (x) B, то A B.

Т.1

. 1) Пусть A B f (x) g(x) - противоречие.

Т.1

2)Пусть A B f (x) g(x) - противоречие.

3) B g(x), 4) B g(x) .

§9. Односторонние пределы. Необходимое и достаточное условия существования предела в точке.

Пусть f (x) определена в U(x0 , ).

Опр.1 Число A lim f (x) наз-ся правым односторонним

x x0

пределом (x x0 ), если:

0 ( ) 0 x x0 x x0 f (x) A .

Опр.2 Число A lim f (x) наз-ся левым односторонним

x x0

пределом (x x0 ), если:

0 ( ) 0 x x0 x x0 f (x) A .

Т.(необходимое и достаточное условие существования предела функции в точке)

lim f (x) A

lim

f (x) lim f (x) A

x x0

. 1)необходимость

Пусть lim

f (x) A : 0 ( ) 0 x

x x0

f (x) A

x x

f (x) A

x x0

x0 x x0

f (x) A

lim f (x) lim

f (x) A.

x x0

2) достаточность

Пусть lim

f (x)

lim

f (x) A. Пусть

0, тогда

x x0

1 ( ) 0 x x0 x x0 1 f (x) A2 ( ) 0 x x0 2 x x0 f (x) A

min{ 1, 2}, 0 x x0 f (x) A ,

lim f (x) A .

x x0

§10. Первый замечательный предел.

Т. (о первом замечательном пределе).

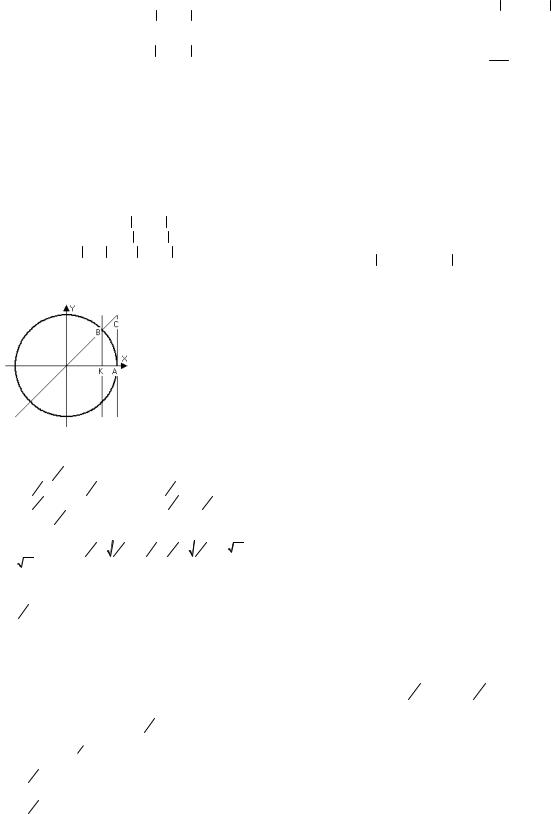
Существует

lim

sin x

x 0

. 1) 0 x

S OBA

OBA

S OCA ,

S OBA

OA BK 1

sin x,

S OBA

R2 x,

1cos x

S OCA 1

2 R2

tg x sin x x tg x 1 xsin x

cos x sin x

1, lim 1 1,

x 0

0 x

cos x 1

lim

cos x 1: 0,

( ) 0

x 0

1 cos x sin x

sin x

, x

lim 1 1

sin x

x 0

lim

lim cos x 1

x 0

sin( t)

sint

2) -

x 0,

lim

1 (2)

x 0

t 0

t 0 t

Из (1) и (2) следует, что lim

sin x

1 .

x 0

Другие замечательные пределы:

lim

tg x

lim

arcsin

1, lim

arctg x

x 0

§11. Второй замечательный предел и связанные с ним пределы.

Т. (1 ) Существует предел

lim

1 1

(1) - второй

замечательный предел.

Сл.1

(1 )lim 1 x 1x e

x 0

ln 1 x

Сл.2

lim

loga

1 x

lim

x 0

ln a

x 0

(2) - третий замечательный предел

Сл.3

lim

ln a

lim

ex 1

x 0

четвертый замечательный предел

Сл.4

lim

1 x

пятый замечательный предел.

x 0

§12. Непрерывность функции в точке. Свойства функций, непрерывных в точке.

Пусть задана f (x) D(y), x0 D(y).	если lim f (x) f (x0 ), т.е.
Опр.1 f (x) - непрерывна в точке x0	если lim f (x) f (x0 ), т.е.
	x x0

0 ( ) 0 x U(x0 , ) f (x) f (x0 ) .

Опр.2 f (x) - непрерывна на мн-ве X, если она непрерывна в каждой точке этого множества.

Т.1 Если функции f (x) и g(x) - непрерывны в т. x0 и g(x) 0, то непрерывны следующие функции.

1) f (x) g(x), 2) f (x) g(x), 3) f (x).

g(x)

. 1) (x) f (x) g(x), lim (x) lim f (x) g(x)

x x0

lim f (x) lim g(x) f (x0 ) g(x0 ) (x0 ).

x x0

lim (x) lim g(x) f (x)

2) (x) g(x) f (x),

x x0

lim g(x) lim

f (x) g(x0 ) f (x0 ) (x0 ).

x x0

f (x0 )

f (x)

3) (x)

, lim (x) lim

(x0 ) .

g(x)

x x0

x x0 g(x)

g(x0 )

Т.2 (о непрерывности сложной функции)

Если y f (x) - непрерывна в точке x0 ,

z g(y) -

- непрерывна в точке y0 f (x0 ), то функция

z g( f (x)) (x) - непрерывна в точке x0 .

lim (x) g( f (x

)) lim g( f (x)) g

lim f (x)

x x0

. Пусть

z g(x) - непрерывна в точке y0

f (x0 ),

тогда ( ) 0 y

y y0

g(y) g(y0 )

. А т.к.

y f (x) - непрерывна

в точке x0

0 ,

( ) 0 x

x x0

f (x) f (x0 )

g( f (x)) g( f (x0 )) . Следовательно z g( f (x)) - - непрерывна в точке x0.

§13 Классификация точек разрыва функции одной переменной.

Пусть задана f (x) и x0 D( f ).

Опр.1 Ф-ия f (x) называется разрывной в точке x0 , если

она не является в этой точке непрерывой. Т.е. lim f (x0 ).

x x0

Опр.2 Точка x0 - точка разрыва 1-го рода ф-ии f (x), если:

а) lim f (x) A, A f (x0 ) - точка устранимого разрыва.

x x0

б) lim f (x) lim f (x) - точка неустранимого разрыва.

x x0	x x0
h(x0 ) lim	f (x) lim f (x) - скачок функции в точке x0.
x x0	x x0

Опр.3 Точка x0 - точка разрыва 2-го рода, если lim f (x)

x x0

или lim f (x) не существует или бесконечен.

x x0

§14. Свойства функций, непрерывных на отрезке.

Опр.1 y f (x) - непрерывна на a,b , если она непрерына в каждой точке a,b , в т.a - непр. справа, в т.b - слева.

Т.1 Если f (x) - непрерывна на a,b и f (a) f (b) 0, то

c a,b f (c) 0.

Т.2 (первая теорема Вейерштрасса)

Если f (x) - непрерывна на a,b , то она на этом отрезке ограничена. A,B (A B) x a,b A f (x) B.

Т.3 (вторая теорема Вейештрасса)

Непрерывная на a,b ф-ия достигает на этом отрезке своих верхних и нижних граней, которые наз-ся соответсвенно наибольшее и наименьшее значения функции на a,b .

Обозн: inf f (x) A, sup f (x) B.

a,b a,b

, a,b A f ( ) min f (x), B f ( ) max f (x).

	a,b					a,b
. По Т.2 f (x)	- ограничена на a,b , т.е.
A, B (A B) x a,b A f (x) B.
Пусть f (x) B. Рассмотрим (x)					1	0. (x) -
- непрерывна на a,b .				B f (x)
			1
B1 0 x a,b (x) B1,					B1	(B1 0),
			B f (x)
B f (x) 1	, f (x) B 1		B - противоречие (B -
B1		B1			достигает своей
не верхняя часть. Следовательно, f (x)

верхней грани B, т.е. a,b f ( ) B max f (x) .

0,B

§15. Обратная функция и ее непрерывность.

Т. Если f (x):

1)определена на a,b , f (a) c, f (b) d,

2)монотонно возрастает(убывает) на a,b

f (a) f (x) f (b) f (b) f (x) f (a) , 3) непрерывна на a,b ,

то на c,d определена обратная функция f 1 (y), монотонно возрастающая (убывающая) и непрерывная на c,d .

x 0

§1. Определение производной. Геометрический и механический смысл производной.

Задача 1. Написать уравнение касательной к графику функции

y f (x)

в точке M0 (x0 , y0 ), y f (x0 ).

MM0 K ,

M1M0 K , x x0 x, y y0 y.

Опр.1 Предельное положение секущей M0 M при x 0

называется касательной к кривой y f (x) в точке x0 .

Рассмотрим

M0 KM. MK y y0 y, M0 K x.

tg k, k tg lim

(1).

x 0

x 0 x

( )

Уравнение касательной: y y0 lim

x x0 (2).

x 0 x

Задача 2. Тело движется прямолинейно S s(t) из точки A.

Найти мгновенную скорость тела в точке B.

В момент t0 тело находилось в точке A. В момент t - в т.B.

t t0 t, s(t) s(t0 ) S, vср

vмгн lim vср lim

(3).

t 0

t 0 t

Пусть y f (x) - определена и непрерывна в окр. точки x.

Дадим x приращение x, так чтобы x x U (x, ).y f (x x) f (x) - приращение функции в точке x.

Опр.2 Конечный предел отношения приращения функции к приращению аргумента при условии, что x 0, наз-ся

производной ф-ии f (x) в точке x, а ф-ия - дифференцируемая


в точке x. lim			y		dy	y (x).

	x 0 x				dx
Т. Если y f (x)				- дифференцируема в точке x0 , то она в
этой точке непрерывна.
tg lim	y	y (x0 ).

x 0 x
Геометрический смысл производной:

Если y f (x) - дифференцируема в точке x0 , то к графику функции в точке M0 (x0 , y0 ) (y0 f (x0 )) можно провести касательную, угловой коэффициент которой будет равен значению производной в точке x0 .


y y0	y (x0 )(x x0 )			- ур-е касательной к кривой в т.M0

y y0		1	x x0		- ур-е нормали к кривой в т.M0

		y (x0 )			производной:
Механический смысл
Производная - это скорость изменения функции в т.M0.

§2.Два определения дифференцируемой в точке функции и их эквивалентность. Дифференциал 1-го порядка и его геометрический смысл.

Опр.1 Функция y f (x) - дифференцируема в точке x0 , если у нее в этой точке есть производная.

Опр.2 Функция y f (x) - дифференцируема в точке x0 , если ее приращение в этой точке можно представить

в виде: y A x (x0 , x) x. A не зависит от x, lim (x0 , x) 0 (б.м.).

Т. Определения 1, 2 о дифференцировании функции в точке эквивалентны.

. 1) 1 2
lim	y	y (x),	y	y (x0 ) ( x),

x 0 x			x

y y (x0 ) x ( x) x, A y (x0 ) функция дифференцируема в смысле опр.2

2) 2 1

y A x ( x) x, y A ( x),x

lim	y	lim A ( x) A y (x0 ) - производная

x 0 x		x 0

существует, следовательно,

y f (x) - дифференцируема в смысле опр.1 . Опр.3 Главная линейная относительно приращения аргумента часть приращения дифференцируемой ф-ии называют дифференциалом 1-го порядка или 1-м дифференциалом этой функции.

y A x ( x) x, A y (x0 ), dy A x y (x0 ) x (2)

dx x, dy y (x0 ) dx

MK y, TK y (x0 ) x dy.

Геометрический смысл дифференциала: дифференциал функции - это приращение точек касательной и кривой y f (x) в точке M0.

y dy d( x) x, f (x) f (x ) dy

малое число

f (x) f (x0 ) dy (3)

(для приближенного вычисления значений функций).

§3. Производные основных элементарных функций.

1) y xn ,n Q.

Дадим x приращение x.

y x x

1 ,

5-й зам.

предел

lim

nxn 1.

x 0 x

x 0

2) y loga x,

a 0,

a 1.

Дадим x приращение x.

y loga x x loga

x loga

1 xx

3-й зам.

loga

предел

lim

xln a

x 0 x

x 0

3) y ax , a 0, a 1.

Дадим x приращение x.

y ax x ax

ax a x 1 ,

a x

4-й зам.

предел

ln a.

lim

x 0 x

x 0

4) y sin x. Дадим x приращение x.

y sin x x sin x 2cos x

sin

cos x x2 sin x2

1-й зам.

предел

cos x.

lim

x 0 x

x 0

5) y cos x. Дадим x приращение x.

y cos(x x) cos x 2sin x

sin

lim

sin x x2 sin x

sin x.

x 0 x

x 0

§4. Правила дифференцирования.

Утв.1 Производная постоянной равна нулю: f (x) C, y f (x x) f (x) C C 0,

lim y 0 C 0

x 0 x

Т.1 Если u(x) и v(x) дифференцируемы в точке x, то их

сумма и разность u(x) v(x) u v (1).

Т.2 Если u(x) и v(x) дифференцируемы в точке x, то их

произведение u(x) v(x) u'v uv' (2).

. Дадим x приращение x.

u(x) u, v(x) v, u u(x x) u, u(x x) u u,

v v(x x) v, м(x x) v v.

Рассмотрим z u(x) v(x).

z u(x x) v(x x) u v

u v v u u v u v u v.

(u v) lim

lim

v u u v u v

lim

x 0 x

x 0

x 0 v

u lim

lim

u v

u v u v .

x 0 x

x 0

Т.3 Если u(x) и v(x) дифференцируемы в точке x, то их

частно	u(x)	u 'v uv'		(3).

		v	2
	v(x)

§5. Дифференцирование обратной и сложной функции.

Т.1 Если y f (x) монотонна и дифференцируема в окр-ти точки x0 и ее производная y (x0 ) 0, то обратная функция x f 1 (y) дифференцируема в точке y0 f (x0 ) и ее


производная		x (y0 )		1		(1).
производная		x (y0 )			y (x0 )	(1).
. Дадим y0		приращение y.
x x(x0 x) x(y0 ),
x (y0 ) lim	x		lim	1			1	.
x (y0 ) lim			lim	y			y (x0 )	.
y 0 y			x 0	y			y (x0 )
					x

Т.2 (о дифференцировании сложной функции).

Если y f (x) дифференцируема в точке x0 , а ф-ия z g(y) дифференцируема в точке y0 f (x0 ), то сложная функция

z g f (x)	дифференцируема в точке x0 и ее производная
z (x0 ) g(y0 ) y (x0 )				(2).
. Дадим x0	приращение				x. Тогда y получит приращение
y f (x0 x) f (x0 ) y y0							, а z g(y) - приращение
z g(y0 y) g(y0 ),						y
z (x0 ) lim	z	lim	z				z (y0 ) y (x0 ) .

					y
x 0 x		x 0				x

§6. Метод логарифмического дифференцирования.

y u(x)v x . Прологарифмируем обе части, получим: ln y v(x)ln u(x). Продифференцируем равенство:

1	y v (x) lnu(x) v(x)				1	u (x),
y				u(x)
			v(x)
y y v		'(x) lnu(x)		u (x)				,
y y v		'(x) lnu(x)	u(x)	u (x)				,
		v x	u(x)
		v x			v(x)
y' u(x)		v'(x) lnu(x)					u		(x) .
y' u(x)		v'(x) lnu(x)					u		(x) .
					u(x)

§7. Производные высших порядков. Бином Ньютона.

Опр.1 Второй производной или производной 2-го порядка ф-ии y f (x) наз-ся производная ее первой производной.

n 1

d2 y

y y ,

y ,

или y

1) y ax ,

y ax ln a,

y ax ln2

... ,

y n

ax lnn a

2) y ln x,

, y

1 2

y 4

1 2 3

... ,

y n

n 1

3) y sin x,

y cos x sin

, y cos

x sin

... ,

sin

4) y

cos x,

Аналогично пункту 3 получаем:

cos

Опр.2 Биномом Ньютона называет n-ая степень двучлена: x a n .

x a n

xn A1xn 1

A2 xn 2 ... Ak xn k

... An 1x An

Продифференцируем обе части равенства:

n x a n 1 nxn 1 A1 n 1 xn 2 A2 n 2 xn 3 ...

n k xn k 1 ... An 1.

Еще раз продифференцируем обе части неравенства:

n n 1 x a n 2

n n 1 xn 2 A1 n 1 n 2 xx 3 ...

... n k n k 1 Ak xn k 2

... 2An 2.

Дифференцируя равенство k-ый раз, получим:

n n 1 ... n k 1 x a n k

n n 1 ... n k 1 xn k

n 1 n 2 ... n k 2 xn k 1

... Ak n k !

n-ое дифференцирование:

n! n!An ,

n n 1 an 2

an An ,

nan 1 An 1,

2An 2 ,...,

n n 1 ... n k 1 an k Ak

n k !

n 1

n n 1 !

n 2

An an ,

An 1 na

An 2

n n 1 n k 1

n k

Ak Cn

n k !

n k

n n 1 ... n k 1

n k !

n 1

n Cn ,

n 1 !

x a n

Cn0 xn a0

Cnn 1xn 1a1 ... Cnk xn k ak ... Cnn x0an

x a n

Cnk xn k ak

- бином Ньютона.

k 0

§8. Дифференцирование функций, заданных параметрически.

Опр. Если функции x(t) и y(t) непрерывны на , , ф-ия x(t) монотонна и имеет обратную ф-ию t(x), то сложная ф-ия F(x) y t(x) наз-ся параметрически заданной ф-ией. F(x) y t(x) - параметрически заданная ф-ия.

(1)	x x(t)
(1)		, t ,b
	y	y(y)

Т. Если x(t) и y(t) дифференцируемы на некотором отрезке, то параметрически заданная функция y t(x) диф-ма

и производная ее равна yx

		dy		dy		yt
. yx				dt			.
				dx
		dx				xt
				dt
yxx	yx x		yxt tx			yx t
	ytt xt xtt yt				(3)
		xt 3

yt (2) xt

ytxt t

1 xt

§9. Основные теоремы дифференциального исчисления.

п.1 Теоремы Ролля и Коши Т.1 (Ролля)

Если y f (x) : 1) определена и непрерна на a,b , 2) дифференцируема на a,b , 3) f (a) f (b), то найдется точка с на a,b такая, что f (c) 0.

Т.2 (Коши) Если f (x) и g(x):

1)определены и непрерывна на a,b ,

2)дифференцируемы на a,b , 3) g(x) 0 на a,b , то существует точка c a,b , такая, что

справедлива формула:	f (b) f (a)	f (c)	(1)
	g(b) g(a)	g (c)

п.2 Теорема Лагранжа и ее геометрический смысл. Т. Если f (x) определена и непрерывна на a,b и

дифференцируема на a,b ,		то существует точка c,
такая, что справедливо:
f (b) f (a) f (c) b a		(2)

. Рассм. вспомогательную ф-ию F(x) f (x) x. F(x) - определена и непрерывна на a,b .

F(x) - диф. на a,b , как разность диф. функций и F (x) f (x) . Подберем так, чтобы F(a) F(b)

F(a) f (a) a F(b) f (b) b,

b a f (b) f (a), f (b) f (a) . b a

При найденном для ф-ии F(x) выполнены все условия теоремы Ролля и по ней существует т.c,

в которой F (c) 0, т.е. f (c) 0, f (c).

f (b) f (a) f (c) . b a

Геометрический смысл теоремы Лагранжа.

C c, f (c) ,	tg	KB	f (b) f (a)	f (c)
		AK
			b a

§10. Условия постоянства и монотонности функций на интервале.

Т.1 Если f (x) - диф. на a,b и f (x) 0	на a,b , то
f (x) const ( f (x) - постоянная)

. Пусть x1 x2 и x1,x2 a,b . Тогда на x1,x2 выполнены все условия Т. Лагранжа, т.е существует точка c x1, x2

f (x2 ) f (x1 ) f (c) x2 x1 , f (c) 0 f (x2 ) f x1 , т.е. f (x) const .

Т.2 (условие возрастания (убывания) функции на интервале)

Если f (x) - диф. на a,b и f (x) 0 f (x) 0 , то f (x)

возрастает (убывает) на a,b .
. (убывание)
Пусть x1,x2 - прозвольные точки принадлежащие a,b		и
x1 x2. По условию f (x) 0 x a,b ,	тогда на x1, x2	для

f (x) выполнены все условия Т. Лагранжа. Следовательно,

f (x2 )	f (x1 ) f (c) x2 x1 0, где c x1, x2
f (x2 )	f (x1). Т.е f (x) убывает на a,b по определению .

§11. Экстремум функции. Необходимые и достаточные условия экстремума.

Пусть задана y f (x) и x0 - внутренняя точка области определения.

Опр.1 В точке x0 функция f (x) имеет максимум(минимум)

при условии, что x U (x0 , ) f (x) f (x0 ) f (x) f (x0 ) Максимум и минимум экстремум

Т.1 (необходимое условие экстремума)

Если y f (x) имеет экстремум в точку x0 , то f (x0 ) 0

или не существует.

Опр.2 Точки, в которых f (x) 0 или не существует, называются критическими (станционарными, подозрительными) по экстремуму.

Т.2 (1-ое достаточное условие экстремума)

Пусть y f (x) - диф. в окрестности критической по экстрему точке, кроме может быть самой этой точки. Тогда: 1) если при переходе черех точку x0 f (x) меняет знак, то в точке x0 есть экстремум, а именно:

а) максимум, если при x x0	f (x) 0	и при x x0
f (x) 0,	f (x) 0
б) минимум, если при x x0	f (x) 0	и при x x0
f (x) 0.

. 1) (минимум) Пусть при переходе через x0 f (x) меняет знак / , тогда по т. Лагранжа:

x c x0 , f (c) 0 f (x0 ) f (x) f (c) x0 x 0

Значит f (x0 ) f (x),

x0 c x, f '(c) 0 f (x) f (x0 ) f (c) x x0 0

Значит f (x) f (x0 ). Следовательно по опр.1 в т.x0 есть экстремум, а именно минимум.

2) Пусть при переходе через т.x0 f (x) 0 постоянно,

т.е x U (x0 , ) f (x) 0. Тогда по т. Лагранжа:

x c x0 , f (x0 ) f (x) f (c) x0 x 0 f (x0 ) f (x), x0 c x, f (x) f (x0 ) f (c) x x0 0 f (x) f (x0 ).

Следовательно по опр.1 экстремума в т.x0 НЕТ . Т.3 (2-ое достаточное условие экстремума)

Если y f (x) имеет f (x) и f (x) в U (x0 , ) и f (x) 0,то

1)если f (x0 ) 0, то в т.x0 - минимум,

2)если f (x0 ) 0, то в т.x0 - максимум.

§12. Наибольшее и наименьшее значения функции на отрезке.

Пусть y f (x) - непрерывна на a,b , тогда по 2-ой теореме Вейерштрасса у нее есть на этом отрезке наибольшее и наменьшее значения. Для нахождения наибольшего и наименьшего значения необходимо:

1)найти критические по экстремуму точки из a,b ,

2)вычислить значения функции в критических точках и на концах отрезка a,b ,

3)из полученных значений выбрать самое большое и самое маленькое.

§13. Выпуклость и вогнутость графика функции. Точка перегиба.

Пусть y f (x) - непрерывна a,b , a x1 x2 b,

A a, f (a) ,B b, f (b) ,C x1, f (x1 ) ,D x2 , f (x2 ) .

Уравнение CD :

y f (x1)

x x1

f (x2 ) f (x1)

x2 x1

x x1 f (x2 ) f (x1 )

f (x1 ),

x2 x1

f (x2 ) x x1 f (x1 ) x2 x

x2 x1

l(x)

f (x2 ) x x1

f (x1 ) x2

(1)

x2 x1

Опр.1 На x1, x2 график ф-ии y f (x) имеет выпуклость

вверх (вниз), если x x1, x2	l(x) f (x)	l(x) f (x) .
Т.1 Если ф-ия y f (x) имеет f	(x) и f (x)	на a,b и

f (x) 0 f (x) 0 , то на a,b ф-ия f (x) имеет выпуклость вниз (вверх).

Опр.2 Точка x0 , при переходе через которую график ф-ии y f (x) сменяет направление выпуклости, называется точкой перегиба ф-ии f (x), а точка M0 x0 , f (x0 ) - точкой перегиба графика функции.

Т.2 (необходимое условие перегиба)

Если в точке x0 функция имеет перегиб, то f (x) 0 или не существует.

Опр.3 Точки, в которых f (x) 0 или не существует называются критическими по перегибу.

Т.3 (достаточное условие перегиба)

Для того чтобы в точке x0 , критической по перегибу, ф-ия f (x) имела перегиб, достаточно, чтобы при переходе через эту точку f (x) меняла знак. Если f (x) знака не меняет, значит в т.x0 перегиба НЕТ.

§14. Асимптоты графика функции. Полное исследование функции и построение ее графика.

Опр.1 Прямая x a называется вертикальной асимптотой графика ф-ии y f (x), если хотя бы один из односторонних пределов lim f (x) или lim f (x) .

x a

Опр.2 Прямая y kx b - невертикальная асимптота графика функции y f (x), если (x) f (x) kx b - б.м. функция при x .

Т. Если y kx b - невертикальная асимптота графика ф-ии

y f (x), то	k lim	f (x)	,	b lim f (x) kx	(1).

	x	x		x

Полное исследование функции и построение графика проводится по следующей схеме:

1.Находим ООФ и вертикальные асимптоты.

2.Точки пересечения графика функции с осями координат.

3.Четность, нечетность, периодичность функции.

4-5. Промежутки монотонности, выпуклости, экстремумы и перегибы.

6.Невертикальные асимптоты графика функции.

7.Построение графика.

§15. Раскрытие неопределенностей. Правила Лопиталя.

п.1 00, первое правило Лопиталя .

Т.1 Если f (x) и g(x):

1) определены и непрерывны на a,b ,

2) существует предел

lim

f (x) lim

g(x) 0,

3) g (x) 0 на a,b ,

x a

4) существует lim

f (x)

x a g (x)

тогда существует lim

f (x)

x a g(x)

п.2 , второе правило Лопиталя

Т.2 Если f (x) и g(x):

1) определены и непрерывны на a,b ,

2) существует предел

lim

f (x) lim

g(x) ,

3) g (x) 0 на a,b ,

x a

4) существует lim

f (x)

x a g (x)

тогда существует lim

f (x)

x a g(x)

п.3 Раскрытие неопределенностей 1 ,0 , 0

lim f (x) g(x)

, y f (x) g(x)

x a

limln y K lim f (x) g(x)

ln y g(x)ln

f (x),

x a

Неопределенности вида ,

0 сводятся к

неопределенностям 0

или

с помощью

алгебраических преобразований.

§1. Первообразная и неопределенный интеграл. Свойства неопределенного интеграла.

Опр.1 Диф. функция F(x) называется первообразной для ф-ии f (x), если F (x) f (x).

Т.1 1) Если ф-ия F(x) - первообразная для f (x), то ф-ия F(x) C также является первообразной для f (x).

2) Если F(x) и (x) - первообразные для f (x), то разность F(x) (x) C (постоянная)

. 1) F(x) f (x), F(x) C f (x) F(x) C -

-первообразная для f (x),

2)Пусть (x) - первообразная для f (x)

F(x) (x) f (x) f (x) 0 по условию постоянства функции это означает, что F(x) (x) C,F(x) (x) C

Опр.2 Множество всех первообразных функции f (x) есть неопределенный интеграл от этой функции.

Обозн:		f (x)dx F(x) X, F '(x) f (x) (1)

подынтегральное

выражение

Геометрический смысл неопределенного интеграла:

Свойства неопределенных интегралов :

1. d f (x)dx f (x)dx

. По опр.1 f (x)dx F(x) C, где F (x)

f (x),

d f (x)dx d F(x) C f (x)dx .

2. d F(x) F(x) C

3. f1(x) f2 (x) dx f1 (x)dx f2 (x)dx (2)

f1(x),

f2 (x),

тогда

. Пусть F1 (x)

F2 (x)

f1 (x)dx F1(x) C, f2 (x)dx F2 (x) C,

F1 (x) F2 (x) - первообразная для

f1(x) f2 (x).

По определению:

f1(x) f2 (x) dx F1(x) F2 (x) C,

f1 (x)dx f2 (x)dx F1(x) F2 (x) C C

f1(x) f2 (x) dx f1 (x)dx f2 (x)dx .

4. Cf (x)dx C f (x),

C const

(доказывается аналогично свойству 3).

§2. Таблица основных интегралов.

xn 1

C,n 1

n 1

3. ax dx

C, ex dx ex C

ln a

4. sin xdx cos x C

5. cos xdx sin x C

tg x C

ctg x C

cos2

sin2

arcsin

arcsin x C

1 x

arctg x C

arctg

1 x2

10.

x a

11.

. 1. 1) x 0, ln

C ln x C

2) x 0,

ln( x) C

arctg

1 x

11. 1) x

x2 a2

ln x

2 x

x x

a2 x

x2 a2

2) x

x2 a2

x2 a

x2 a2

2 x2 a2

x2 a2

§3. Интегрирование по частям в неопределенном интеграле.

Т. Если u(x) и v(x) - диф. и существует интеграл vdu,

то существует интеграл

udv uv vdu

. По правилу дифференцирования произведения:

d u v u dv v du, d u v udv vdu,

u v udv vdu,

udv u v vdu .

Рекурентная формула:

n 2x

)

n 1

dv dx,

v x

x2dx

n 1

2na2

, In 1

n 1

2n 1

(2)

n 1

2na2 x2 a2 n

2na2

§4. Замена переменной в неопределенном интеграле.

Т. (о замене переменной)

Если F(x) - первообразная ф-ии f (x) на множестве X и x (t) - дифференцируемая функция, значение которой принадлежит мн-ву X , то ф-ия F( (t)) - первобразная для ф-ии f ( (t)) (t) и интеграл

f ( (t)) (t)dt f (x)dx ,

ф-ия x (t) называется подстановкой.

. Пусть f (x)dx F(x) C. Покажем, что

F( (t)) F ( (t)) (t) f ( (t)) (t),

f ( (t)) (t)dt F( (t)) C F(x) C f (x)dx .

§5 Интегрирование рациональных функций.

п.1 Интегрированиепростейших рациональных функций.

Опр.1 Рациональной функцией называется отношение двух многочленов

f (x) Pm (x) , где Pm (x) - многочлен степени m,

Qn (x)

Pm b0 xm b1xm 1 ... bm 1x bm ,b0 0,

Qn (x) - многочлен степени n с C 1 перед xn ,

Qn (x) xn a1xn 1 ... an 1x an.

Если m n, то f (x) - неправильная рациональная функция, а если m n, то f (x) - неправильная рациональная (дробно-рациональная) функция.

Опр.2 Простейшими рациональными функциями называются

правильные рациональные функции следующих видов:

A,a R

II.

m N m 1

x a

Bx C

III.

p,q,c R

q 0

IV.

x2 px q

d(x a)

Aln

x a

II.

d(x a)

x a

1 m x

m 1

x a

III. Преобразуем x2

px q x2

x p 2 2

q p2

4 , t x p 2 , a2 q p2

4 , x2 px q t2 a2

x t p

,dx dt

B t p

2 C

px q

tdt

C Bp

ln t

2 a2

arctg

ln x2

px q

C Bp

arctg

x p

q p

IV.

B t p

2 C

dt B

tdt

c Bp

px q

ln t

0 далее

a2 m

используем рекурентную формулу и возвращаемся к подстановке.

п.2 Интегрированиеправильных рациональных функций.

f (x)

Pm (x)

m n,

Qn (x) xn

a1xn 1

... an 1x an ,

Qn (x)

- кратности 2 ,

1i - кратности s1.

a1 - кратности 1,

Это означает, что Qn (x) делится на x2

p1x q1

2i - кратности s2. Тогда Qn (x)

делится на x2

p2 x q2

тогда

x2 p1x q1

x2 p2 x q2

Qn (x) x a1 1

x a2

Т.1 Правильная рациональная функция вида

Pm (x)

2 x2 p1x q1

x2 p2 x q2

a1 1

x a1

...

A 1

...

B 2

1 1

x a1

x a2

x a1

x a2

M1x N1

...

M s1 x Ns1

P1x L1

...

x2 p1x q1 s1

x2 p1x q1

x2 p2 x q2 s

Ps2

x Ls2

, где A ,..., A , B ,..., B

,...,M

,..., N

,P,...,P ,

x2 p2 x q2

L1,...,Ls1

- неопределенные коэффициэнты (метод неопределенных

коэффициентов).

Т.2 Правильная рациональная функция имеет первообразные, которые выражены через правильные рациональные функции, логарифмы и арктангенсы.

п.3 Интегрированиенеправильных рациональных функций

f (x)

Pm (x)

,m n, f (x) f1(x)

Rm n (x)

Qn (x)

Rm n (x)

прав. рац. ф-ия

f (x)dx f1(x)dx

dx.

(x)

метод неопр. коэф.

п.4 МетодОстроградского

f (x)

Pm (x)

, m n,

Qn (x)

p1x q1

p2 x q2

где

Qn (x) x a1 1 x a2 2

Pm (x)

P1 (x)

P2 (x)

1 2 s1 s2

(1) где

Qn (x)

Q1(x)

(x)

метод неопр. коэф.

1 1

2 1

p1x q1

s1 1

p2 x q2

s2 1

Q1 (x) x a1

Q2 (x)

Qn (x)

, P1 (x) и P2 (x) - многочлены в степени на 1 меньше

Q1 (x)

чем Q1 (x) и Q2 (x) соответственно. Продифференцируем формулу (1):

Pm (x) P1 Q1 PQ1 1 .

Qn (x) Q1 (x) 2

§6 Вычисление интегралов вида:

ax b

x, n

cx d

ax b

R x, n

- рациональное выражение от x и

cx d

ax b

Подстановка t n

ax b

ctn x dtn

ax b,

cx d

b dtn

dn tn 1 ctn a cn tn 1 b dtn

, dx

ctn a

ctn a 2

ntn 1 d ctn a c b dtn

ntn 1 bc ad

dt,

ctn a 2

b dtn

n 1 bc ad

ax b

x, n

dx n

,t t

dt.

cx d

§7. Интегрирование выражений вида

Rx, ax2 bx c . Подстановка Эйлера.

1.ax2 bx c не имеет действительных корней.

( ) ax2 bx c xa t - 1-ая подстановка Эйлера. ax2 bx c ax2 2xat t2 , x b 2t a t2 c,

2t b 2t

t2 c 2

b 2t

b 2t a

2bt 2t2

at2 c a

dt,

b 2t

b 2t a

тогда R x,

at2

ax2 bx c

b 2t

t2 c

at2 c

2bt 2t2

b 2t a

b 2t

b 2t a

2. ax2

bx c a x x1

x x2

x1,x2

- корни.

x x1

x x2

R x,

dx R x,

ax2 bx c

x x1

a x x2

x x

dx.

x x1

a x x2

( ) - 2-ая подстановка

x x1

ax2

xt2 x1t2 ax ax2 ,

x t2 a x1t2 ax2 , x

x1t

x1t2

ax2

x1t2 ax1

a x1 x2

x x

2x1t t2 a 2t x1t2 ax2

2ta

dt,

a 2

t2 a 2

x x2

x, x x1

x x1

x1t2 ax2

t x2 x1

x1 x2

dt - рациональное

выражение.

§8 Вычисление интегралов вида

Pn (x)

ax2

bx c

Pn (x)

Pn 1 (x)

bx c

(1),

bx c

- неизвестный коэффициент,

Pn 1 (x) - многочлен степени n 1

с неопр. коэффициентами.

Дифференцируем формулу, чтобы получить Pn (x)

Pn (x)

Pn 1 (x) 2ax b

Pn 1 (x) ax

bx c

ax2 bx c

2 ax2 bx c

ax2

bx c

2Pn (x) 2Pn 1 (x) ax2 bx c Pn 1(x) 2ax b 2 , xn

xn 1 (n 1) уравнения с (n 1) неизвестными ( )

...

Решение системы уравнений ( ) в (1), в которой последний интеграл - табличный.

§9 Интегрирование тригонометрических функций.

п.1Вычисление cos xcos xdx,

sin xsin xdx,

sin xcos xdx

Преобразуем подынтегральные функции:

cos xcos x

cos

( )x cos ( )x ,

sin xsin x

cos

( )x cos ( )x ,

( )x sin ( )x

sin xcos x

sin

далее вычисления сводятся к табличным интегралам.

п.2 Вычисление sinm xcosn

xdx, m,n Q

1) m 2k 1 (нечетное),

тогда

sinm xcosn

xdx sin2k

xsin xcosn

xdx

1 cos2

cosn xsin xdx

t cos x

1 t2

dt sin xdx

2) n 2k 1 (нечетное), тогда sinm

xcos2k 1

рац. выражение

sinm xcos2k

xcos xdx 1 sin2

x k sinm

xcos xdx

t sin x

1 t2

dt cos xdx

tm dt - рац. выражение от t

m 2k,

2s (четные), тогда

sin2k xcos2s

xdx 12k s

1 cos2x k 1 2cos2x s

dx, далее

см. п.1,2,3.

п.3 Вычисление R sin x,cos x dx.Универсальная

тригонометрическая подстановка.

t tg

( ),

x 2arctgt,

2dt

1 t2

2tg x

sin x 2sin

cos

2tg

cos2

2 1 tg

2 x

1 t2

2 x

1 t2

cos x cos

sin

cos

x 1 tg

1 t

1 t2

2dt

R sin x,cos x dx R

1 t

§10. Определение интеграла по Риману. Ограниченность интегрируемой функции.

Пусть f (x) определена на a,b . Разобьем a,b на частичные отрезки с помощью точек деления.

Обозн. разбиения: : a x0	x1 ... xk ... xn	b,
Длина k-го отрезка xk xk 1 xk , k 0,1,2,..., n 1 ,
На каждом отрезке выберем точку Ck xk ,xk 1 ,		тогда
n 1
f (Ck ) xk f (C0 ) x0	f (C1) x1 ... f (Cn 1 ) xn 1,
k 0

max xk	- диаметр разбиения ,
k

Опр. Конечный предел интегральных сумм при 0, не зависящий ни от разбиения отрезка a,b на частичные отрезки, ни от выбора точек Ck , называется определенным интегралом от a до b ф-ии f (x), а сама ф-ия - интегрируемой

на a,b .		b
на a,b .	lim		f (x)dx	(2)
	0
		a

Утв.1 Если ф-ия f (x) интегрируема на a,b , то она на этом отрезке ограничена.

Утв.2 Если f (x) - неотрицательная и интегрируемая на a,b ,

то f (x)dx SaABb (площади криволинейной трапеции,

ограниченной сверху графиком f (x), снизу - осью абсцисс, и прямыми x a, x b.

§11. Верхняя и нижняя интегральные суммы и их свойства. Необходимые и достаточные условия интегрируемости функции по Риману.

Пусть задана f (x),		x a,b .
Разобьем a,b : a x0			x1 .. xk ..xn	b,
Длина k го отрезка xk			xk 1 xk ,
Обозначим mk :		inf f (x), Mk : sup f (x),
	xk ,xk 1		xk ,xk 1
	n 1

s mk xk
(1)	k 0
	n 1

S Mk x
	k 0

(1) - нижняя и верхняя интегр. суммы Дарбу,

n 1

Ck xk ,xk 1 , ( ) s S, f (Ck ) xk

k 0

Св.1 Если к фиксированному разбиению добавить новые точки, то нижняя сумма Дарбу может только увеличиться, а верхняя только уменьшиться.

Св.2 Нижняя сумма Дарбу не превосходит верхней, даже если эти суммы отвечают разным разбиениям. Добавим к новые точки ( 0),

s1,s2 ,...,sn - монотонно возрастает, sn Si , S1,S2 ,...,Sn - монотонно убывает, Sn si ,

I sup sn , I inf Sn , s I I S

Т. (необходимое и достаточное условие интегрируемости функции по Риману)

Для того чтобы органиченная на a,b ф-ия f (x) была интегрируема на a,b по Риману необходимо и

достаточно:		lim s lim S		b	f (x)dx
достаточно:	lim S s 0	lim s lim S			f (x)dx
	0	0	0
				a

§12. Свойства неопределенного интеграла.

Св.1 f (x)dx 0

Св.2 f (x)dx f (x)dx

Св.3 f (x) g(x) dx f (x)dx g(x)dx

Св.4 Cf (x)dx C f (x)dx (C - постоянная)

Св.5 если a c b, то

f (x)dx

f (x)dx f (x)dx

(аддитивность определенного интеграла)

Св.6 Если f (x) g(x), то f (x)dx

g(x)dx

Св.7 Если f (x) - интегрируема на a,b ,

то

f (x)

интегрируема на a,b ,

то

f (x)dx

f (x)

Св.8 Если f (x) - интегр. на

то

a,b и m f (x) M ,

m b a f (x)dx M b a

Теорема о среднем для опр. интеграла.

§13. Интеграл с переменным верхним пределом и его свойства. Основная формула интегрального исчисления.

Пусть f (x) опр. и огран. на a,b . Возьмем xk так, что a x b, на a, x - f (x) интегрируема.

(1) F(x) f (x)dx - интеграл с перем. верхний пределом

Св.1 Если f (x) интегр. на a,b , то F(x) - непр. на a,b .

. Зафикс. x a,b , дадим x приращение x,

			x x	x
F(x) F(x x) F(x) f (x)dx f (x)dx
x	x x		a	a
x	x x		x	x x
f (x)dx f (x)dx f (x)dx				f (x)dx,
a	x		a	x
				x x
По усл. m f (x) M			(св.8), m x	f (x)dx M x,
		1	x x	x
			x x
разделим на x:			f (x)dx , m M ,
разделим на x:		x	f (x)dx , m M ,
x x		x	x
x x
	f (x)dx x, F(x) x, x 0, F(x) 0
x
F(x) - непрер. в точке x .
Св.2 Если f (x) - непр. на a,b , то F(x) - диф. функция,
	x
F (x) f (x), f (x)dx f (x)
	a

. Фикс. x, даем приращение x, F x, m M , по т. о среднем для непр. ф-ии f (x) сущ. точка

c x,x x ,			такая что f (c) f (x) f (c) x,
F (x) lim		F		lim f (c) f (x),
	x 0	x		x 0
x
f (x)dx		f (x) .
a	x
Сл. Непр. на отрезке ф-ия f (x) всегда имеет

первообразную, одной из которых является интеграл с переменным верхним пределом.

Т. (Основная формула интегрального исчисления, ф. Ньютона-Лейбница)

Если f (x) - непр. на a,b , то f (x)dx (b) (a),

где (x) - какая-нибудь первообразная f (x),

f (x)dx (b) (a) (x) ba (2)

. (x) - первообр. f (x), F(x) f (x)dx - первобр. f (x)

x	a
	b

(x) f (x)dx C, (a) C, f (x)dx (a),

a	a
b

f (x)dx (b) (a) .

§14. Интегрирование по частям в определенном интеграле.

Т. Если u(x) и v(x) - диф. на a,b , то

	b		ba	b
	udv uv			vdu
	udv uv			vdu
	a			a
§15. Замена переменной в определенном
интеграле.				- интегр. на a,b	и x (t) - диф. на , ,
Т. Если f (x)				- интегр. на a,b	и x (t) - диф. на , ,
где ( ) a,				( ) b, то

	b	b
	f (x)dx f (t) (t)dt
	a	a

§16. Вычисление площадей в прямоугольной декартовой системе координат.

Рассм. плоскую фигуру ограниченную сверху графиком

ф-ии y f (x)				- непр. на a,b , а снизу - y g(x) -
непр. на a,b . Разобъем a,b :
: a x0 x1				... xk		... xn b,
xk		xk 1	xk	, k 0,1,..., n 1 ,			max xk ,
m		min	f (x), M			max f (x),	m	k
								min g(x),
	k	xk ,xk 1			k	xk ,xk 1	k	xk ,xk 1

Mk max g(x).

xk ,xk 1

Рассм. ступенчатую фигуру F из прямоугольников с осн.xk и высотами hk mk Mk .

n 1

F ABCD, S(F) mk Mk xk mk xk Mk xk

sf	Sg ,	k 0						k 0	k 0
sf	Sg ,
рассм. ступенчатую фигуру F1 из прямоугольников с осн.
xk	и высотами hk Mk		mk .
	n 1
S(F1 ) x Mk mk Sf						sg
	k 0
Опр.1 Если lim S(F) lim S(F1), то плоская фигура ABCD
	0	0
называется квадрируемой, а общее значение этих пределов
называется площадью фигуры ABCD.
					b		b
lim S(F) lim sf		lim Sg				f (x)dx		g(x)dx
0	0	0
b					a		a
b
f (x) g(x) dx ( )
a					b
					b	f (x) f (x) dx ( )
lim S(F1 ) lim Sf		lim sg				f (x) f (x) dx ( )
0	0	0
					a
Из равенств ( ) и ( ) фигура ABCD - квадрируемая и
						b
площадь ее в дек. пр. с.к				S f (x) g(x) dx					(2)
						a
§17. Вычисление площадей в полярной системе
координат.							x rsin
Формулы перехода из пол. в дек. с.к.							x rsin
Формулы перехода из пол. в дек. с.к.									,
							y r cos

Рассм. плоскую фигуру в пол. с.к. ограниченную 2-мя лучами и графиком непр. на a,b функции r ( 0 ). Разобъем

0 1 ... k

k 1

... n

. Обозначим: mk

min

r( ),

max

k , k 1

r( ). Рассмотрим круговые сектора, опирающиеся на

k , k 1

углы k и ограниченные дугами окружности радиуса mk .

Площадь каждого кругового сектора Sсек 1

R2d,

n 1

mk2

- нижняя сумма Дарбу для ф-ии

( ).

2 k 0

Рассмотрим круговые сектора, опирающиеся на углы k

ограниченные дугами окружности радиуса Mk :

n 1

Mk2 k

- верхняя сумма Дарбу для ф-ии

( ),

2 k 0

lim s lim

n 1

r2 ( )d , limS 1

( )d .

k 0

S12 r2 ( )d (1) - ф. для вычисления площади в пол. с.к

§18. Объем тела вращения.

Рассм. тело V, обладающее следующими свойствами:

1)расположено по одну сторону от плоскости

2)в сечении тела плоскостями, параллельными пл-ти, лежат квадрируемые фигуры.

3)площадь сечения, проведенного на расстояние x от пл-ти , пл-тью парал. - непр. ф-ия S(x).

4)Если S(x2 ) S(x1), то проекция фигуры с площадью S(x2 ) на пл-ть содержит проекцию фигуры с с площадью S(x1) на пл-ть .

Опр.1 Пространственное тело, обладающее св-ми 1-4 называется регулярным.

Т.1 Регулярное тело кубируемое и объем го вычисляется

по формуле V S(x)dx, где S(x) - площадь сечения,

проведенного на расстоянии x от пл-ти ,

a- наименьшее расстояние от тела до пл-ти ,

b- наибольшее расстояние от тела до пл-ти .

Т.2 Если тело V получено вращением криволинейной трапеции ограниченной сверху графиком ф-ии y f (x), f (x) 0, а снизу отрезком a,b вокруг оси Ox , то его

объем V f (x) 2 dx (2)

. Покажем, что тело V - регулярное.

x a,b , S(x) r2 f (x) 2 непр. ф-ия от x,

Все условия (1-4) выполнены V- регулярное тело,

Тогда по ф.(1): y f (x), f (x) 0, a x b,

V f (x) 2 dx .

Сл. Если криволинейная трапеция вращается вокруг Oy , то объем полученного тела вычисляется по формуле:

V 2 x f (x)dx (3)

1 / 21 2 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.05.2015186.45 Кб75Мат. анализ. часть 2.docx
#
10.05.2015288.1 Кб32Мат. анализ. часть1.docx
#
17.11.2019477.7 Кб16Мат. лог. (Л-3).doc
#
23.11.2019753.15 Кб9Мат. лог. (Л-4).doc
#
23.11.2019699.39 Кб23Мат. лог.(Л-5).doc
#
10.05.20152.7 Mб57матан ( шпора ).pdf
#
10.05.20152.8 Mб39матан ( шпора) .pdf
#
10.05.2015160.12 Кб35матан3.pdf
#
10.05.2015273.92 Кб49матан_теория.doc
#
18.12.2018107.04 Кб35Математика 3.docx
#
20.04.20191.01 Mб100Материалы к Госэкзамену (Оценка стоимости инвес....doc