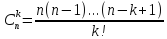Глава 1. Элементы теории множеств. Последовательности.
Лекция 1. Элементы теории множеств. Грани числовых множеств. Абсолютная величина числа. Бином Ньютона.
Множество - одно из основных понятий математики.
Опр.1.1. Множество – совокупность объектов, собранных по какому-либо признаку, который называется характеристическим свойством. Объекты, из которых состоит множество, называются его элементами.
Числовыми множествами называются множества, элементами которых являются числа.
Приняты следующие обозначения:
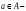 элемент
элемент
 принадлежит множеству
принадлежит множеству
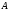 ;
;
 элемент
элемент
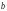 не принадлежит множеству
не принадлежит множеству
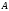 ;
;
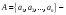 множество
множество
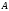 состоит из элементов
состоит из элементов
 .
.
Опр.1.2.
Два
множества
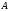 и
и
 называются равными
называются равными
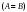 ,
если они состоят из одних и тех же
элементов. Множество
,
если они состоят из одних и тех же
элементов. Множество
 называется подмножеством
множества
называется подмножеством
множества
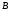
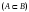 ,
если все элементы множества
,
если все элементы множества
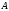 являются одновременно и элементами
множества
являются одновременно и элементами
множества
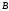 .
.
Множество,
не содержащее ни одного элемента,
называется пустым
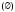 .
.
Пересечением
множеств
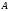 и
и
 называется множество
называется множество
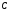 ,
состоящее из всех элементов, одновременно
принадлежащих как
,
состоящее из всех элементов, одновременно
принадлежащих как
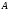 ,
так и
,
так и
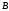 ,
т.е.
,
т.е.
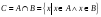 .
.
Объединением
множеств
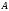 и
и
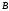 называется множество
называется множество
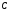 ,
состоящее из всех элементов, принадлежащих
хотя бы одному их данных множеств, т.е.
,
состоящее из всех элементов, принадлежащих
хотя бы одному их данных множеств, т.е.
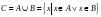 .
.
Разностью
множеств
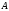 и
и
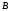 называется множество
называется множество
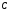 ,
состоящее из тех элементов множества
,
состоящее из тех элементов множества
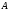 ,
которые не принадлежат множеству
,
которые не принадлежат множеству
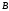 ,
т.е.
,
т.е.
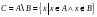 .
.
В представленных записях операций со множествами нами использованы так называемые «кванторы» - логические символы, с помощью которых удобно записывать многие математические понятия:
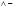 «и»;
«и»;
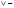 «или»;
«или»;
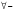 квантор
общности, означает «для любого», «для
каждого»;
квантор
общности, означает «для любого», «для
каждого»;
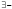 квантор
существования, вместо слов «существует»,
«имеется»;
квантор
существования, вместо слов «существует»,
«имеется»;
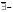 «не
существует»;
«не
существует»;
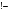 «единственный»;
«единственный»;
 «следует»;
«следует»;
 «равносильно»,
«тогда и только тогда».
«равносильно»,
«тогда и только тогда».
Числа,
используемые для счета предметов или
объектов, называются натуральными
 .
Если к натуральным числам присоединить
им противоположные и ноль, то мы получим
множество целых чисел
.
Если к натуральным числам присоединить
им противоположные и ноль, то мы получим
множество целых чисел
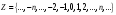 .
Множество всех дробных чисел получило
название рациональных чисел
.
Множество всех дробных чисел получило
название рациональных чисел
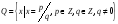 .
Каждое рациональное число может быть
записано в виде конечной десятичной
дроби. Множество бесконечных непериодических
десятичных дробей получило название
иррациональных чисел, например
.
Каждое рациональное число может быть
записано в виде конечной десятичной
дроби. Множество бесконечных непериодических
десятичных дробей получило название
иррациональных чисел, например
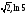 и т.д. Все рациональные и иррациональные
числа образуют множество действительных
чисел
и т.д. Все рациональные и иррациональные
числа образуют множество действительных
чисел
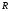 .
.
Опр.1.3. Прямая линия, на которой указаны начало отсчета длин, масштаб и направление отсчета, называется числовой осью.
Между числовой осью и множеством действительных чисел существует взаимооднозначное соответствие, т.е. каждому действительному числу соответствует единственная точка на прямой и наоборот, каждой точке на прямой ставится в соответствие единственное действительное число.
Опр.1.4.
Интервалом
называется множество всех точек (чисел),
заключенных между двумя какими-нибудь
точками (числами), называемыми концами
интервала. Если вместе с множеством
точек интервала рассматривать и его
концы, то интервал называется замкнутым
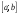 или
или
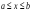 .
Если концы интервала не рассматривать,
то интервал называется открытым
.
Если концы интервала не рассматривать,
то интервал называется открытым
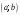 или
или
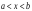 .
Если один конец присоединяется к
интервалу, а другой – нет, то получаем
полуоткрытый
интервал
.
Если один конец присоединяется к
интервалу, а другой – нет, то получаем
полуоткрытый
интервал
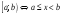 или
или
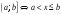 .
Кроме конечных интервалов, существуют
бесконечные
интервалы,
например
.
Кроме конечных интервалов, существуют
бесконечные
интервалы,
например
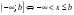 ;
;
 ;
;
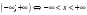 и т.д.
и т.д.
Опр.1.5.
Абсолютной
величиной (модулем)
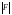 числа
числа
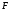 называется число, равное самому себе,
если
называется число, равное самому себе,
если
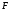 положительно или равно нулю, и ему
противоположное, если
положительно или равно нулю, и ему
противоположное, если
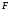 отрицательно:
отрицательно:
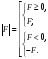
Отметим некоторые свойства модуля:
-
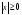 .
. -
 .
. -
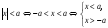 ;
;
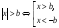 .
. -
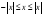 .
. -
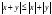 ,
,
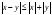 .
. -
 ,
,
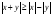 .
. -
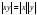 ,
,
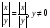 .
.
Опр.1.6.
Открытый
интервал
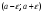 длины
длины
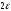 с центром в точке
с центром в точке
 называется
называется
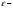 окрестностью
точки
окрестностью
точки
 .
Иначе множество действительных чисел
.
Иначе множество действительных чисел
 ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
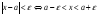 называется
называется
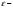 окрестностью
точки
окрестностью
точки
 .
.
Опр.1.7.
Точка
 называется предельной
точкой множества
называется предельной
точкой множества
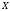 ,
если в любой
,
если в любой
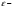 окрестностью
точки
окрестностью
точки
 находятся точки из
находятся точки из
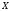 ,
отличные от
,
отличные от
 .
Изолированной
точкой множества
.
Изолированной
точкой множества
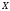 называется такая точка
называется такая точка
 этого множества, что в достаточно малой
ее
этого множества, что в достаточно малой
ее
 окрестности
нет точек из
окрестности
нет точек из
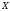 ,
отличных от
,
отличных от
 .
Внутренней
точкой множества
.
Внутренней
точкой множества
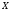 называется такая точка
называется такая точка
 этого множества, что существует некоторая
этого множества, что существует некоторая
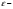 окрестность
точки
окрестность
точки
 ,
целиком содержащаяся в множестве
,
целиком содержащаяся в множестве
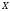 .
Множество, все точки которого являются
внутренними, называется открытым;
множество, содержащее все свои предельные
точки называется замкнутым.
Точка
.
Множество, все точки которого являются
внутренними, называется открытым;
множество, содержащее все свои предельные
точки называется замкнутым.
Точка
 называется граничной
точкой множества
называется граничной
точкой множества
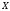 ,
если любая ее
,
если любая ее
 окрестность
содержит точки, как принадлежащие
множеству
окрестность
содержит точки, как принадлежащие
множеству
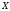 ,
так и не принадлежащие ему. Множество
всех граничных точек множества
,
так и не принадлежащие ему. Множество
всех граничных точек множества
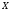 называется
границей
этого
множества.
называется
границей
этого
множества.
Опр.1.8.
Множество
 ограничено
сверху (снизу),
если существует такое число
ограничено
сверху (снизу),
если существует такое число
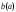 ,
что
,
что
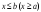 для любого
для любого
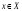 .
В этом случае число
.
В этом случае число
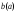 называется верхней
(нижней) гранью множества
называется верхней
(нижней) гранью множества
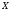 .
Множество, ограниченное и сверху и
снизу, называется ограниченным,
в противном случае – неограниченным.
.
Множество, ограниченное и сверху и
снизу, называется ограниченным,
в противном случае – неограниченным.
Опр.1.9.
Наименьшая из всех верхних граней
называется точной
верхней гранью множества
и обозначается
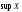 .
Наибольшая из всех нижних граней
называется точной
нижней гранью множества
и обозначается
.
Наибольшая из всех нижних граней
называется точной
нижней гранью множества
и обозначается
 .
Если множество
.
Если множество
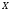 не ограничено сверху, то
не ограничено сверху, то
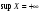 ;
если не ограничено снизу, то
;
если не ограничено снизу, то
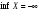 .
.
Теорема1.1. Всякое ограниченное сверху (снизу) числовое множество имеет точную верхнюю (нижнюю) грань.
Бином Ньютона.