-
Предельный переход в неравенствах
Лемма
3.2:
Если последовательность
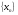имеет
предел а>0 (<0), то, начиная с некоторого
номера N,
выполняется неравенство
,
т.е. члены последовательности сохраняют
знак а.
Следствие:
Если
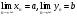и
a<b,
то, начиная с некоторого номера N,
выполняется xn<yn.
Теорема
3.5 (о сохранении знака):
Пусть
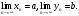Если,
начиная с какого-то номера N,
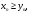то
и a≥b.
Теорема
3.6 (предел промежуточной последовательности):
Пусть для последовательностей
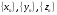выполнены
неравенства
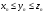и
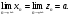Тогда
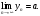
4. Монотонные последовательности. Число e
Опр.3.2.
Последовательность {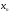
}
называется возрастающей, если хn
<
xn+1
для
любого n;
неубывающей, если xn
≤
xn+1
для
любого n;
убывающей, если xn
>
xn+1
для любого n;
невозврастающей, если xn
≥
xn+1
для
любого n.
Все
такие последовательности называются
монотонными. Возрастающие и убывающие
последовательности называются также
строго монотонными.
Монотонные
последовательности ограничены по
крайней мере с одной стороны: неубывающая
ограничена снизу (xn
≥
xn+1
для
любого n);
невозрастающая ограничена сверху (xn
≤
Xn+1
для
любого n).
Оказывается,
если монотонная последовательность
ограничена с обеих сторон, то она
сходится. Немонотонные последовательности
этим свойством не обладают.
Теорема3.6
(о
сходимости монотонной, ограниченной
последовательности):
Для того, чтобы монотонная последовательность
сходилась, необходимо и достаточно,
чтобы она была ограниченной.
Число
е:
Его
обозначают e
=
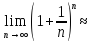2, 718281, число иррациональное (число
Эйлера).
5.
Теорема
о вложенных отрезках.
Опр.3.3.
Пусть
дана последовательность отрезков [a1,
b1],
[a2,
b2],
… , [an,
bn],
… таких, что любой последующий содержится
в предыдущем [a1,
b1]
[a2,
b2]
[an,
bn]
;
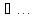т.е. an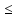
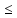an+1
bn+1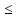
bn
для любого n,
и пусть
.
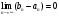Будем называть эту последовательность
последовательностью вложенных отрезков.
Теорема3.7(о вложенных отрезках): Для любой последовательности вложенных отрезков существует только одна точка, принадлежащая всем отрезкам этой последовательности. Замечание: теорема неверна, если вместо отрезков рассматривать интервалы.