
Краткий курс математического анализа. Том 2
.pdf
60Гл. 4. Дифференциальное исчисление функций многих переменных
Оп р е д е л е н и е 2. Пусть функция f определена на произведении
X × Y множеств X Rn и Y Rn, x X, y Y , y(0) Y.
Функция f (x, y) называется равномерно стремящейся к нулю на множестве X при y → y(0), если для любого ε > 0 существует такое δ > 0, что для всех точек x X и всех y U (y(0); δ) ∩ Y выполня-
ется неравенство
|f (x, y)| < ε.
В случае равномерного стремления функции f (x, y) к нулю на множестве X при y → y(0) пишут f (x, y) 0, y → y(0).
X
Равномерное стремление функции f (x, y) к нулю на множестве X при y → y(0) имеет место тогда и только тогда, когда
lim |
, |
0 |
y y(0) |
sup |f (x |
y)| = . |
→ |
x X |
|
Действительно, пусть y U (y(0); δ) ∩ Y. Тогда, если |f (x, y)| < ε, x X, то sup |f (x, y)| ε, а если sup |f (x, y)|< ε, то и |f (x, y)| < < ε,
x X. |
x X |
x X |
|
|
Подробно понятие равномерного стремления функции к пределу на множестве будет изучаться в п. 49.1.
З а м е ч а н и е 2. Если X Rn, X — компакт, d > 0, Xd = |
||
= {x : ρ(x, X) d}, функция f непрерывна на Xd и ε(x, |
x) = f (x + |
|
+ x) − f (x), |
x X, | x| d и, следовательно, x + |
x Xd, то |
функция ε(x, |
x) равномерно стремится к нулю на компакте X при |
|
x → 0.
Согласно замечанию 2 в п. 33.4 множество Xd также является компактом, а поэтому непрерывная на нем функция f равномерно непрерывна. Это означает, что для любого ε > 0 существует такое δ > 0, что для всех точек x Xd, x + x Xd, | x| < δ, выполняется неравенство
|ε(x, x)| = |f (x + x) − f (x)| < ε.
В частности, это верно для всех x X и | x| < δ, если выбрать δ < d, что и означает равномерное стремление к нулю функции ε(x, x):
ε(x, |
X |
|
→ |
0. |
|
x) 0, |
x |
|
|
Сделанное замечание показывает связь понятий равномерной непрерывности и равномерного стремления к нулю. На этой связи основано доказательство нижеследующей теоремы.
Для простоты записи вернемся снова к функциям двух переменных.

§ 36. Частные производные |
61 |
Т е о р е м а 4. Если функция f имеет непрерывные частные производные на открытом множестве G R2 и
f (x + x, y + y) − f (x, y) = |
∂f (x, y) |
x + |
|
∂f (x, y) |
y + ερ, |
||||||
|
|
|
|||||||||
∂x |
|
∂y |
|||||||||
то функция ε = ε(x, y, |
|
x, |
y) равномерно стремится к нулю на |
||||||||
любом компакте X G при ρ = |
x2 + |
y2 → 0, (x, y) X. |
|||||||||
Пусть |
X |
— компакт, |
X |
|
G. Множество Rn |
\ |
G замкнуто (см. лем- |
||||
|
|
|
|
|
|
|
|||||
му 6 в п. 33.3) и не пересекается с компактом X, поэтому (см. теорему 6 в п. 33.4) множества X и Rn \ G находятся на положительном
расстоянии:
d = ρ(X,Rn \ G) > 0.
Пусть Xd/2 = M G : ρ(M , X) d2 . Поскольку множество X — компакт, то и множество Xd/2 — компакт (см. замечание 2 в п. 33.4). Ясно, что
X Xd/2 G.
Частные производные fx и fy функции f , будучи непрерывными на компакте Xd/2, равномерно непрерывны на нем (см. следствие теоремы 2 в п. 35.1) Поэтому для любого η > 0 существует такое
δ > 0, что для любых точек (x, y) Xd/2 и (x + x, y + y) Xd/2, |
|||||||||||||||||
у которых |
x2 + y2 < δ, |
выполняются неравенства |
|
|
|||||||||||||
|
|
|
|
|
|
|fx(x + x, y + y) − fx(x, y)| < η, |
(36.22) |
||||||||||
|
|
|
|
|
|
|fy(x + x, y + y) − fy(x, y)| < η. |
|
|
|||||||||
|
|
При доказательстве теоремы |
3 |
было показано (см. |
форму- |
||||||||||||
лы (36.21)), что в равенстве |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
f = fx(x, y)Δx + fy(x, y)Δy + ε1 x + ε2 y, (x, y) G, |
|||||||||||||
бесконечно малые функции ε1 = ε1(x, y, x, y) и ε2 = ε2(x, y, |
x, y), |
||||||||||||||||
|
|
|
|
|
→ 0, задаются формулами: |
|
|
||||||||||
|
|
x2 + y2 |
|
|
|||||||||||||
|
|
|
|
ε1 = fx(x + θ1 x, y + y) − fx(x, y), 0 < θ1 < 1, |
|
|
|||||||||||
|
|
|
|
|
|
ε2 = fy(x, y + θ2 y) − fy(x, y), 0 < θ2 < 1. |
|
|
|||||||||
|
|
|
|
|
|
|
|
d |
|
|
|||||||
|
|
Если M = (x, y) X и |
|
|
x2 + |
y2 < |
, то точки M1 |
= (x + |
|||||||||
+ θ |
+ θ |
2 |
|||||||||||||||
1 |
, |
y + |
, |
|
2 |
y) |
содержатся в компакте |
X |
d/2: |
||||||||
|
|
x |
y) и M2 = (x |
y |
|
|
|||||||||||
|
|
|
|
|
|
M1 Xd/2, |
M2 Xd/2. |
|
|
||||||||

62 Гл. 4. Дифференциальное исчисление функций многих переменных
Действительно, |
x2 + y2 < |
|
|
|
|
|
|
|
|||||||||||||||
ρ(M , M1) = |
|
|
|
|
|
|
d |
, |
|
|
|
|
|||||||||||
(θ1 x)2 + y2 |
|
|
|
|
|||||||||||||||||||
2 |
|
|
|
|
|||||||||||||||||||
ρ(M , M2) = |
|
|
|
|
|
x2 + y2 < |
d |
. |
|
|
|
|
|
|
|
|
|||||||
(θ2 y) |
|
|
|
|
|
|
|
|
|||||||||||||||
|
2 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
+ |
|
2 |
|
|||
Если взять δ0 > 0 такое, что δ0 < δ и δ0 |
< |
|
, то при |
x |
|
y |
|
< |
|||||||||||||||
|
|
|
|||||||||||||||||||||
< δ0 будем иметь |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||
ρ(M , M1) < δ0 < |
d |
, ρ(M , M2) < δ0 |
< |
d |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
и, следовательно, M1 Xd/2, M2 Xd/2. Поэтому в силу (36.22) при |
||
|
|
|
x2 + y2 < δ0 выполняются неравенства |
||
|
|
|ε1| < η, |ε2| < η, |
что и означает равномерное стремление к нулю функций ε1 и ε2 при |
|||||||||||||||
|
|
y2 → 0. |
|
|
|
|
|
|
|
|
|
|
|
||
ρ = |
x2 + |
ε(x, y, |
|
|
|
y) |
следующим |
образом |
|||||||
Определим |
функцию |
|
x, |
||||||||||||
(ср. с (36.14)): |
|
|
|
|
x |
|
|
y |
|
|
|
|
|
||
|
|
|
|
def |
ε |
+ ε |
|
при |
ρ = 0, |
|
|
||||
|
ε(x, y, |
x, |
|
|
ρ |
|
|
||||||||
|
y) = |
1 |
ρ |
2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
0 |
|
|
при |
ρ = 0. |
|
|
||
Тогда |ε| |ε1| + |ε2| |
и ε1 x + ε2 |
y = ερ, |
а следовательно, |
|
|
||||||||||
|
f (x + x, |
|
|
, |
|
= |
, |
|
|
, |
y)Δy + ερ |
, |
|||
|
|
y + y) − f (x |
y) (36.19) fx(x |
y)Δx + fy(x |
|
||||||||||
|
|
|
|
|
(36.20) |
|
|
|
|
|
|
|
|||
при этом для всех (x, y) X при ρ < δ выполняется неравенство |
|||||||||||||||
|
|
|
|
|
ε < 2η, |
|
|
|
|
|
|
||||
что |
и означает |
равномерное |
|
стремление к |
нулю |
функции |
|||||||||
ε = ε(x, y, x, |
y) на компакте X при ρ → 0. |
|
|
|
|
||||||||||
З а м е ч а н и е 3. Определения дифференцируемости функции и ее дифференциала в точке обобщаются на случай функции любого числа переменных, обобщенной в некоторой окрестности этой точки.
Дифференцируемость |
функции |
y = f (x), |
x = (x1, ..., n), в |
точке |
||||||||||||
x(0) = (x(0) |
, |
... |
, xn(0)) |
означает, |
что ее приращение |
y = f (x(0) + |
x) |
− |
||||||||
1 |
|
|
(0) |
|
|
|
|
(0) |
|
|
|
|||||
− f (x(0)), где x(0) + |
x = (x1 |
+ x1, |
..., |
xn |
+ |
xn), представимо |
||||||||||
в виде |
|
|
|
|
y = dy + o(ρ), ρ → 0, |
|
|
(36.23) |
||||||||
где |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
∂f (x(0)) |
|
|
|
2 |
|
|
|
|
|
|
|
||||
dy = |
|
∂xi |
dxi, |
ρ = |
|
|
xi , |
dxi = |
xi, i = 1, 2, ..., n. |
|
||||||
i=1 |
|
|
|
|
|
i=1 |
|
|
|
|
|
|
(36.24) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

§ 36. Частные производные |
63 |
Функция (36.24) при выполнении условия (36.23) называется дифференциалом функции f (x) в точке x(0), а также полным дифферен-
циалом, в отличие от дифференциалов
∂f
dxi f = ∂xi dxi
функции f (x) по отдельным переменным xi, i = 1, 2, ..., n, которые называются частными дифференциалами.
Теоремы 1–4 переносятся на случай функций любого числа переменных.
З а м е ч а н и е 4. Функция, имеющая непрерывные частные производные на некотором множестве, называется непрерывно дифференцируемой на этом множестве. В силу теоремы 3 непрерывно
дифференцируемая на множестве функция дифференцируема на нем.
36.3. Дифференцирование сложной функции. Рассмотрим вначале вопрос о дифференцируемости композиции функции двух переменных и функции одной переменной.
Те о р е м а 5. Если функции x = x(t) и y = y(t) дифференцируемы
вточке t0, а функция z = f (x, y) дифференцируема в точке (x0, y0),
где x0 = x(t0), y0 = y(t0), то сложная функция f (x(t), y(t)) дифференцируема в точке t0 и в этой точке
dz |
= |
∂z dx |
+ |
∂z |
|
dy |
. |
(36.25) |
|||
|
|
|
|
|
|
|
|||||
dt |
∂x dt |
|
|
||||||||
|
|
∂y dt |
|
||||||||
Отметим, что при выполнении условий теоремы в некоторой окрестности точки t0 сложная функция заведомо имеет смысл. В самом деле, согласно определению дифференцируемости функция f определена в некоторой окрестности U точки (x0, y0). Из дифференцируемости же функций x(t) и y(t) в точке t0 следует, что они, а следовательно, и отображение (x(t), y(t)), ставящее в соответствие числу t точку плоскости (x(t), y(t)), определены в некоторой окрестности точки t0 и непрерывны в самой этой точке. Отсюда и из замечания 2 из п. 34.5 сразу следует, что сложная функция f (x(t), y(t)) определена
в некоторой окрестности точки t0. |
|
|
||||||||||
В силу дифференцируемости функции f в точке (x0, y0) |
имеем |
|||||||||||
(обозначения x, y, |
z |
и |
ρ см. в п. 36.2) |
|
||||||||
z = |
∂z |
|
x + |
∂z |
|
|
y + ε1 x + ε2 y, |
(36.26) |
||||
∂x |
∂y |
|||||||||||
(36.9) |
|
|
|
|
|
|||||||
(36.15) |
|
|
|
|
|
|
|
|
|
|
|
|
|
lim ε1 = lim ε2 = 0, |
(36.27) |
||||||||||
|
ρ→0 |
|
|
ρ→0 |
|
|||||||
где частные производные |
∂z |
|
и |
∂z |
|
берутся в точке (x0, y0). |
|
|||||
∂x |
∂y |
|
||||||||||
|
|
|
|
|
|
|
||||||

64 Гл. 4. Дифференциальное исчисление функций многих переменных
Выберем теперь |
x и y специальным образом: задав произвольно |
||
(достаточно малое) |
t, положим |
|
|
x = x(t0 + t) − x(t0), |
y = y(t0 + t) − y(t0). |
(36.28) |
|
В силу непрерывности функций x(t) и y(t) в точке t0 имеем
lim |
x = lim y = 0, а поэтому |
|
|
|
|||
t→0 |
t→0 |
|
|
|
|
|
|
|
lim ρ = |
lim |
x2 |
+ y2 |
= 0. |
(36.29) |
|
|
t→0 |
t→0 |
|
|
|
|
|
Следовательно, согласно теореме 6 о пределе композиции функций (п. 34.5) из равенств (36.27) и (36.29) получим
|
|
|
lim ε1 = |
lim ε2 = 0. |
(36.30) |
||||
|
|
|
t→0 |
|
|
t→0 |
|
t = 0. Тогда в силу |
|
Поделим обе части равенства (36.26) на |
|||||||||
существования в точке t0 конечных производных |
|||||||||
|
dx |
= |
lim |
x |
, |
dy = |
lim |
y |
|
|
|
|
t |
||||||
|
dt |
0 |
t |
dt |
0 |
||||
|
|
|
t→ |
|
|
|
t→ |
|
|
выражение, которое получится в правой части равенства (36.26), будет иметь конечный предел:
lim |
z |
= lim |
|
∂z x |
+ |
∂z y |
+ ε |
x |
+ ε |
y |
= |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
t |
∂x t |
∂y t |
t |
|
|
|
|
|
|
|
||||||||||||||
t→0 |
t→0 |
|
1 |
2 |
t (36.30) |
|
|
|
|
t=t0 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(36.30) |
|
|
|
+ |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
dz |
∂x dt |
∂y |
dt |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
∂z dx |
|
∂z dy |
, |
|||||
т. е. будет существовать производная |
dt |
и для нее будет справедлива |
||||||||||||||||||||||
формула (36.25). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
З а м е ч а н и е 1. Если в условиях теоремы 1 вместо дифференцируемости функций x = x(t) и y = y(t) в точке t0 потребовать лишь, чтобы они были дифференцируемы справа (слева) в этой точке, то при сохранении прочих условий теоремы сложная функция f (x(t), y(t)) будет также дифференцируема справа (слева) в точке t0 и будет спра-
ведлива формула (36.25), если только под производными dzdt , dxdt , dydt понимать производные справа (слева).
З а м е ч а н и е 2. Если функции x = x(u, v), y = y(u, v) дифференцируемы в точке (u0, v0) и, следовательно, имеют в этой точке част-
ные производные |
∂x |
, |
|
∂x |
, |
|
∂y |
, |
∂y |
(теорема 2), а функция z = f (x, y) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
∂u |
|
∂v |
∂u |
∂v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
дифференцируема в точке (x0, y0), где x0 = x(u0, v0), y0 = y(u0, v0), то |
|||||||||||||||||||||||||||||||||
в точке (u0, v0) существуют и частные производные |
∂z |
, |
∂z |
сложной |
|||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
функции z = f (x(u, v), y(u, v)) и |
|
|
|
|
|
|
|
|
|
∂u |
∂v |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
∂z |
= |
∂z |
|
∂x |
|
+ |
∂z |
|
∂y |
, |
|
∂z |
= |
∂z |
|
∂x |
+ |
∂z |
|
∂y |
. |
|
|
(36.31) |
||||||||
|
∂u |
∂x ∂u |
|
|
|
∂v |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
∂y ∂u |
|
|
∂x ∂v |
∂y ∂v |
|
|
|
|
|||||||||||||||||||||
§ 36. Частные производные |
65 |
Доказательство того, чти при сделанных предположениях сложная функция f (x(u, v), y(u, v)) определена в некоторой окрестности точки (u0, v0), проводится аналогично случаю, рассмотренному в теореме 5.
Формулы же (36.31) сразу следуют из формулы (36.25), так как, зафиксировав одно из переменных, u или v, мы окажемся в условиях теоремы 5: сложная функция f (x(u, v), y(u, v)) будет функцией одной
переменной. |
|
|
|
|
|
|
|
|
|
|
З а м е ч а н и е 3. |
Формула (36.31) обобщается на случай функ- |
|||||||||
ций любого числа переменных: если функция y = y(x), |
x = (x1, ... |
|||||||||
..., xn), дифференцируема в точке |
x(0) = (x1(0), ..., xn(0)), |
а функции |
||||||||
xi = xi(t), t = (t1, ..., tm), дифференцируемы в точке t(0) = (t1(0), ..., tm(0)) |
||||||||||
и xi(0) = xi(t(0)), i = 1, 2, ..., n, то сложная функция y(x(t)) имеет |
||||||||||
в точке t(0) частные производные |
|
∂y |
и |
|
||||||
∂tj |
|
|||||||||
|
|
|
n |
|
|
|||||
|
|
|
i |
|
|
|||||
|
∂y |
= |
|
∂y |
|
∂xi |
, |
j = 1, 2, ..., m. |
(36.32) |
|
|
∂tj |
|
=1 |
∂xi ∂tj |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
36.4. Инвариантность формы первого дифференциала.
Аналогично случаю одной переменной запись дифференциала функции многих переменных имеет один и тот же вид как относительно независимых, так и зависимых переменных.
Т е о р е м а 6. Если функции xi = xi(t), t = (t1, ..., tm), i = 1, 2, ...
..., n, имеют в точке t(0) = (t1(0), ..., tm(0)) непрерывные частные произ- |
|||||||||||
водные, а функция y = f (x), |
x = (x1, ..., xn), — непрерывные частные |
||||||||||
производные в точке x(0) = (x1(0), ..., xn(0)), где xi(0) = xi(t(0)), |
i = 1, 2, ... |
||||||||||
..., n, то сложная функция f (x(t)) дифференцируема в точке t(0) и |
|||||||||||
|
m |
|
|
|
|
n |
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
||
dy = |
|
∂f (x(t(0))) |
dtj = |
|
|
∂f (x(0)) dxi, |
|
||||
|
=1 |
∂tj |
|
i=1 |
|
∂xi |
|
||||
короче, |
|
|
|
|
|
|
|
|
|||
|
m |
|
|
|
|
n |
|
|
|
|
|
|
|
j |
∂y |
dtj = |
|
∂y |
|
(36.33) |
|||
|
dy = |
|
|
|
|
dxi. |
|||||
|
=1 |
∂tj |
i=1 |
∂xi |
|
||||||
|
|
|
|
|
|
|
|
||||
Заметим, что из непрерывности частных производных функции следует дифференцируемость этой функции, поэтому в условиях теоремы функции f (x) и xj (t) дифференцируемы соответственно в точках x(0) и t(0). Согласно определению дифференцируемости функция f определена в некоторой окрестности точки x(0). Из дифференцируемости же функций xj (t) следует их непрерывность в точке t(0), а поэто-
def , ,
му непрерывность в этой точке и отображения x(t) = (x1(t) ... xn(t)). Отсюда, согласно замечанию 2 из п. 34.5, следует, что в некоторой окрестности точки t(0) определена сложная функция f (x(t)), о которой идет речь в теореме.
3 Л. Д. Кудрявцев

66 Гл. 4. Дифференциальное исчисление функций многих переменных
Из формулы (36.32) и непрерывности частных производных
∂y |
, |
∂xi |
, i = 1, 2, ..., n, j = 1, 2, ..., m, следует, что сложная функция |
|
|
||
∂xi |
∂tj |
||
y = f (x(t)) имеет в точке t(0) непрерывные частные производные
∂y , j = 1, 2, ..., m, и, следовательно, она дифференцируема.
∂tj
Первое равенство (36.33) следует из определения дифференциала (см. теорему 2 и формулу (36.24)). Докажем второе равенство:
m |
|
|
m |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
∂y ∂xi |
|
|
|
|
|
|
|
|
|
|
|
|
|||
dy = |
|
dtj |
= |
i=1 |
|
|
|
|
dt |
j |
= |
|
|
|
|
|
|
||
(36.24) j=1 |
∂tj |
(36.32) j=1 |
∂xi ∂tj |
|
|
j |
n |
|
|
|
|||||||||
|
|
|
|
|
n |
|
|
|
m |
|
|
|
|
|
|
||||
|
|
|
|
|
|
∂y |
|
|
∂xi |
|
|
∂y |
|
|
|||||
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
dt |
= |
|
dx |
. |
|
|
|
|
|
|
i=1 ∂xi |
j=1 ∂tj |
(36.24) i=1 |
∂xi i |
|
||||||||||
Здесь после того как дифференциал dy был записан по формуле (36.24) через приращения dtj = tj независимых переменных t1, t2, ..., tm, были использованы формулы (36.32) для производных сложных функций. После этого был изменен порядок суммирования
по индексам i и j, а затем снова были использованы формулы (36.24), но уже для функций xi = xi(t), t = (t1, ..., tm), i = 1, 2, ..., n.
Подчеркнем, что в формуле (36.33) дифференциалы dtj являются дифференциалами независимых переменных и поэтому совпадают с их приращениями tj , a dxi — дифференциалы функций; они, вообще говоря, не совпадают с приращениями xi переменных xi.
Свойство дифференциала, выражаемое формулой (36.33), называется инвариантностью формы дифференциала: дифференциал запи-
сывается одинаковым образом, использованы ли в его записи дифференциалы зависимых или независимых переменных.
36.5. Геометрический смысл частных производных и дифференциала. Рассмотрим снова для простоты функцию двух пере-
менных z = f (x, y). Пусть |
она имеет |
||||
в точке (x0, y0) частную производную |
|||||
|
∂f (x0, y0) |
df (x, y0) |
x=x0 |
|
|
|
|
= dx |
= tg α, |
||
|
∂x |
|
(36.34) |
||
|
|
|
|
|
|
где α, согласно геометрическому |
смыслу |
||||
производной функции одной переменной f (x, y0), является углом между осью x и касательной к графику этой функции (рис. 7), т. е. к кривой
z = f (x, y), |
y = y0, |
в точке (x0, y0, z0), |
где z0 = f (x0, y0). |
В этом и состоит геометрический смысл частной производной.
|
|
|
|
|
§ 36. Частные производные |
|
67 |
||||||||||
Вспомним теперь, что дифференцируемость функции z = f (x, y) |
|||||||||||||||||
в точке (x0, y0) означает, что |
|
|
|
|
|
|
|
|
|
||||||||
z = |
∂f (x0, y0) |
|
x + |
∂f (x0, y0) |
y + o(ρ), |
ρ = |
x2 |
+ y2 → 0, |
|||||||||
|
∂x |
|
|
∂y |
|
|
|||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(36.35) |
|
x = x − x0, |
|
y = y − y0, |
z = z − z0. |
(36.36) |
||||||||||||
|
|
|
|||||||||||||||
Подставив (36.36) в равенство (36.35), получим |
|
|
|||||||||||||||
z = z0 + |
∂f (x0, y0) |
(x − x0) + |
∂f (x0, y0) |
(y |
− y0) + o(ρ), ρ |
→ 0. (36.37) |
|||||||||||
|
∂x |
|
|
∂y |
|
|
|||||||||||
Плоскость, определяемая уравнением |
|
|
|
|
|||||||||||||
|
z = z0 + |
∂f (x0, y0) |
(x − x0) + |
∂f (x0, y0) |
(y |
− y0), |
(36.38) |
||||||||||
|
|
|
∂x |
|
|
|
∂y |
|
|||||||||
называется касательной плоскостью к графику функции z = f (x, y) |
|||||||||||||||||
в точке (x0, y0, z0). Если ее аппликату обозначить zкас, то формулу |
|||||||||||||||||
(36.37) можно записать в виде |
|
|
|
|
|
|
|
|
|
||||||||
|
|
z − zкас = o(ρ), |
ρ → 0, |
z = f (x, y), |
|
||||||||||||
т. е. разность между аппликатами графика функции и касательной |
|||||||||||||||||
плоскости является бесконечно малой более высокого порядка, чем ρ |
|||||||||||||||||
при ρ → 0. Плоскость z = z0 + A(x − x0) + B(y − y0), удовлетворяю- |
|||||||||||||||||
щая такому условию, единственна, ибо это условие равносильно диф- |
|||||||||||||||||
ференцируемости функции и коэф- |
|
|
|
|
|
|
|
||||||||||
фициенты A и B уравнения та- |
|
|
|
|
|
|
|
||||||||||
кой плоскости совпадают с коэффи- |
|
|
|
|
|
|
|
||||||||||
циентами дифференциала, которые, |
|
|
|
|
|
|
|
||||||||||
будучи |
равными |
|
соответствующим |
|
|
|
|
|
|
|
|||||||
частным производным, определены |
|
|
|
|
|
|
|
||||||||||
однозначно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Равенство (36.38) можно запи- |
|
|
|
|
|
|
|
||||||||||
сать (см. (36.36)) в виде |
|
|
|
|
|
|
|
|
|
|
|
||||||
zкас − z0 = |
∂f (x0, y0) |
x + |
|
|
|
|
|
|
|
|
|
|
|
||||
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
+ ∂f (x0, y0) |
y |
= dz. |
|
|
|
|
|
|
|
||||||
|
|
|
|
∂y |
|
(36.10) |
|
|
|
|
|
|
|
|
|||
Таким образом, дифференциал функции равен приращению аппликаты касательной плоскости к гра-
фику функции:
dz = zкас − z0.
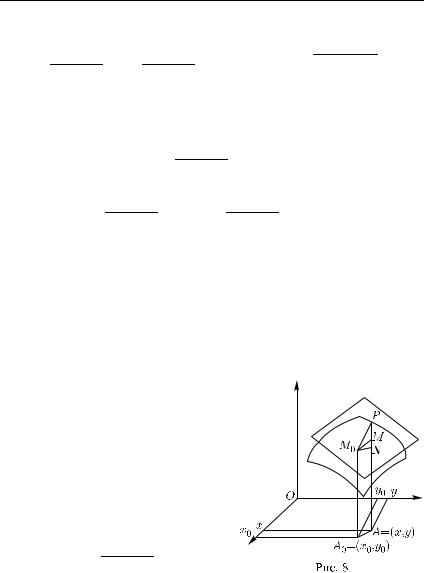
На рис. 8
A0 = (x0, y0), A = (x, y) = (x0 + x, y0 + y),
z0 = f (x0, y0) = A0M0 = AN , z = f (x, y) = AM , zкас = AP
3*
68 Гл. 4. Дифференциальное исчисление функций многих переменных
и, следовательно, |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
dz = N P = AP − AN = zкас − z0, |
|
|
|
|||||
|
|
|
|
|
AM − AP = o(ρ), ρ = A0A → 0. |
|
|
|
|||||
36.6. Производная по направлению. Градиент. |
Пусть |
||||||||||||
функция |
f (x, y, z) определена |
в |
окрестности |
точки |
(x0, y0, z0) |
||||||||
и задан |
вектор |
l = 0. Обозначим через cos α, |
cos β |
и |
cos γ его |
||||||||
направляющие |
косинусы, |
т. е. |
координаты |
единичного |
вектора |
||||||||
|
|
|
|
|
l0 = l/|l| в направлении вектора l: |
|
|
||||||
|
|
|
|
|
|
|
l0 = (cos α, cos β, cos γ). |
|
(36.39) |
||||
|
|
|
|
|
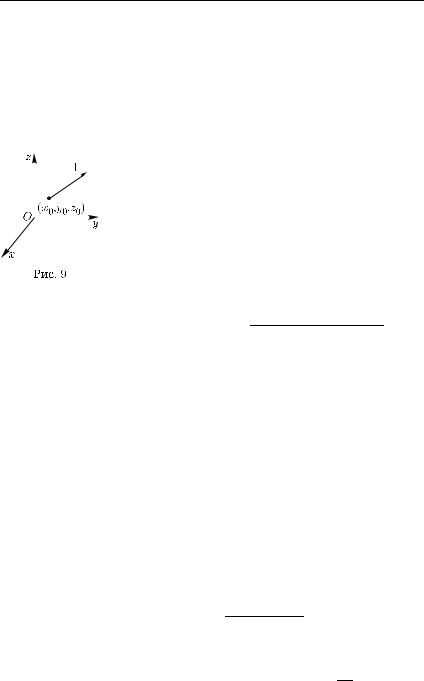
Проведем через точку (x0, y0, z0) луч в направ- |
||||||||
|
|
|
|
|
лении вектора l |
(рис. 9) и запишем его уравнение |
|||||||
|
|
|
|
|
в параметрическом виде: |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
x = x0 + t cos α, y = y0 + t cos β, |
|
(36.40) |
||||||
|
|
|
|
|
|
z = z0 + t cos γ, |
t 0. |
|
|||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
Так |
как |
cos2 α + cos2 β + cos2 γ = |
1, то из |
|||||
формул (36.40) следует, что |
|
|
|
|
(36.39) |
|
|||||||
|
|
|
|
|
|
|
|||||||
|
|
|
= t cos2 α + cos2 β + cos2 γ = t, |
||||||||||
(x − x0)2 + (y − y0)2 + (z − z0)2 |
|||||||||||||
т. е. значение параметра t |
равно расстоянию от точки (x, y, z) лу- |
||||||||||||
ча (36.40), соответствующей этому значению параметра, до точки
(x0, y0, z0).
Рассмотрим сужение функции f на луч (36.40), т. е. композицию
функций f (x, y, z) и функций (36.40): |
|
f (x0 + t cos α, y0 + t cos β, z0 + t cos γ), t 0 |
(36.41) |
(она определена для всех достаточно малых t). Производная справа
этой функции в точке t = 0 |
называется производной функции f |
||||||
в точке (x0, y0, z0) no направлению вектора l и обозначается |
∂f |
: |
|||||
|
|||||||
|
|
|
|
|
+ t cos β, z0 + t cos γ) t=0. |
∂l |
|
|
∂f def |
d |
(36.42) |
||||
|
∂l = |
dt f (x0 + t cos α, y0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В правой части этого равенства стоит производная функции одной переменной. Если M0 = (x0, y0, z0), а M = (x, y, z) — точка луча (36.40) и, следовательно, |M0M | = t, то
∂f (M0) |
= lim |
f (M ) − f (M0) . |
(36.43) |
||
∂l |
|||||
(36.42) t→+ |
0 |
t |
|
||
|
|
|
|
||
Так как все величины в правой части этого равенства не зависят от выбора системы координат (они определяются функцией f , точ-
кой M0 и вектором l), то производная по направлению ∂f∂l в точке M0

§ 36. Частные производные |
69 |
функции f , аргументом которой является точка пространства, не зависит от выбора системы координат.
Если существует не только предел справа (36.43), но и двусторонний
предел lim |
f (M ) − f (M0) |
, то он называется производной по прямой |
|
0 |
|
t |
|
t→ |
y = y0 + t cos β, z = z0 + t cos γ, −∞ < t < +∞. |
||
x = x0 + t cos α, |
|||
Функции (36.40) линейны по t и поэтому, очевидно, дифференцируемы. Следовательно, если функция f дифференцируема в точке (x0, y0, z0), то сложная функция (36.41) дифференцируема в точке t = 0 (теорема 5 из п. 36.3). Вычислив ее производную по формуле производной сложной функции (см. (36.25)), получим
|
|
|
|
|
|
|
∂f |
= |
|
∂f dx |
+ |
∂f |
dy + |
∂f |
|
|
dz |
, |
|
|
(36.44) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
∂x dt |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
∂l |
|
|
|
|
∂y dt |
∂z dt |
|
|
|
|
|
|||||||||||||||||
где, в силу (36.40), |
dx |
= cos α, |
dy |
|
= cos β, |
|
dz |
= cos γ. |
|
||||||||||||||||||||||||||
|
|
dt |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|||||||||||||
Подставив эти выражения в формулу (36.44), будем иметь |
|||||||||||||||||||||||||||||||||||
|
|
|
|
∂f |
= |
∂f |
|
cos α + |
∂f |
cos β + |
∂f |
cos γ. |
(36.45) |
||||||||||||||||||||||
|
|
|
|
∂l |
∂x |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
∂z |
|
|
|
|
|
|||||||||||||||
Здесь значения частных производных |
∂f |
, |
|
|
∂f |
|
, |
∂f |
|
взяты в точке |
|||||||||||||||||||||||||
∂x |
|
|
∂y |
|
∂z |
||||||||||||||||||||||||||||||
(x0, y0, z0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
∂f |
|
∂f |
|
|
∂f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вектор |
, |
, |
|
называется градиентом функции f (в точке, |
|||||||||||||||||||||||||||||||
|
∂y |
∂z |
|||||||||||||||||||||||||||||||||
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
в которой взяты значения частных производных) и обозначается либо |
|||||||
|
|
|
|
|
|
|
|
grad f , либо f (читается «набла эф»). Таким образом, |
|
||||||
|
def |
∂f |
∂f |
∂f |
|
||
|
grad f ≡ f = |
∂x , |
|
, |
|
. |
(36.46) |
|
∂y |
∂z |
|||||
Использовав понятие градиента и скалярного произведения, формулу (36.45) для производной по направлению можно записать следующим образом:
|
∂f |
|
∂f |
|
∂f |
∂f |
|
|
|
|
|
|
|
|||||
|
|
|
= |
|
cos α + |
|
cos β + |
|
cos γ = ( f , l0) = |
|
|
|||||||
|
∂l |
∂x |
∂y |
∂z |
|
|
||||||||||||
|
|
|
|
|
|
|
|
= |f ||l0| |
cos ( |
|
f l |
) |
= |
f |
cos ϕ, (36.47) |
|||
|
|
|
|
|
|
|
|
|
0 |
|
(36.39) |
| | |
|
|||||
где |
ϕ — угол между векторами |
и l, |
или, что то же, между |
|||||||||||||||
f |
||||||||||||||||||
векторами f |
и l0 = l/|l|. |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Из формулы (36.47) видно, что градиент функции не зависит от |
|||||||||||||||
выбора системы координат, как это могло бы показаться из определения (36.46). Если f = 0, то направление градиента f является единственным направлением, по которому в данной точке производ-
ная по направлению ∂f∂l имеет наибольшее значение (оно достигается при ϕ = 0, т. е. когда cos ϕ = 1), а длина градиента f равна этому
