
- •Ргр № 1 (0,138 зе) Пределы: а) Раскрытие неопределенностей б) Непрерывность. Точки разрыва
- •Содержание работы
- •Ргр № 2 (0,138 зе) Техника дифференцирования
- •Содержание работы
- •Контрольные вопросы
- •Ргр № 3 (0,417 зе) Основные методы интегрирования
- •Содержание работы
- •Ргр № 4 (0,278 зе) Применение определенного интеграла к решению задач геометрии и физики
- •Содержание работы
- •Контрольные вопросы
- •Содержание работы
- •Содержание работы
- •Содержание работы
- •Контрольные вопросы
- •Содержание работы
- •Кривые второго порядка
- •14.Векторная функция скалярного аргумента. Векторы скорости и ускорения. Кривизна плоской кривой.
- •Содержание работы
- •Содержание работы
- •7.1. Основная учебная литература
- •7.2. Дополнительная учебная литература, книги издательства «Лань»
- •Математика
Содержание работы
Запись дифференциалов первого и второго порядков для функции двух и трех переменных
Задачи на локальный экстремум
Задачи на условный экстремум
Наибольшее и наименьшее значения функции в замкнутой ограниченной области
Литература [1,2,17]
Элементы теории
Вычисление частных производных производится по тем же правилам, что и вычисление функций одной переменной, считая все переменные постоянными, кроме той, по которой ведется дифференцирование.
Первым
дифференциалом![]() называют
линейную относительно приращений
называют
линейную относительно приращений
![]() часть полного приращения функции,
которая для функции двух переменных
имеет вид:
часть полного приращения функции,
которая для функции двух переменных
имеет вид:
![]()
![]() ,
,
а для функции трех переменных:
![]() .
.
Производная по
направлению задает
скорость изменения функции в заданной
точке по заданному направлению
![]() :
:
![]() .
.
Градиентом дифференцируемой функции называют вектор, координатами которого являются частные производные в заданной точке:
![]() .
.
Производная по направлению является проекцией вектора градиента на это направление:
![]() .
.
Анализ последнего выражения показывает, что градиент является направлением, скорость изменения функции вдоль которого максимальна.
Касательная
плоскость содержит
касательные ко всем кривым, проходящим
через данную точку поверхности
![]() :
:
![]() .
.
Производную
сложной функции
![]() находим
по правилу
находим
по правилу
![]() ,
,
а
производные сложной функции
![]()
![]()
![]() согласно
правилу:
согласно
правилу:
![]()
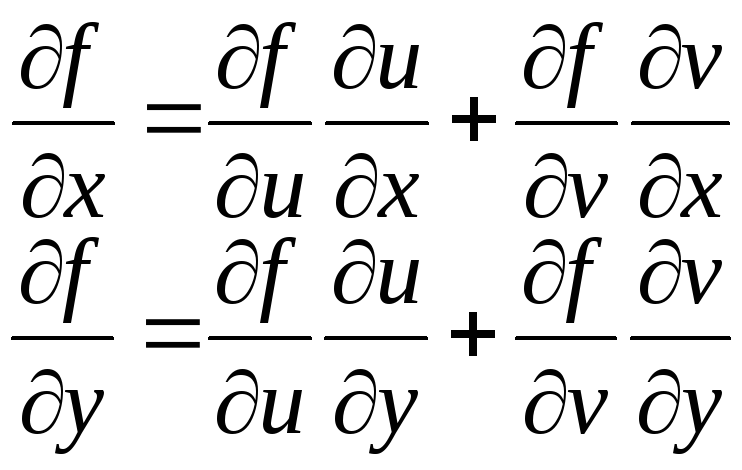 .
.
Производную
функции,
заданной неявно
![]() ,
находят согласно правилу:
,
находят согласно правилу:
![]() .
.
Для
функции
![]() определеныпроизводные
второго порядка:
определеныпроизводные
второго порядка:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Для
функции
![]() ,
кроме указанных выше производных,
определены следующие производные
второго порядка:
,
кроме указанных выше производных,
определены следующие производные
второго порядка:
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Заметим, что в точках непрерывности смешанные частные производные равны.
Дифференциалы второго порядка определяются согласно соотношениям:
![]() ,
,
![]() .
.
Формула
Тейлора в
окрестности точки
![]() с точностью до бесконечно малых второго
порядка имеет вид:
с точностью до бесконечно малых второго
порядка имеет вид:
![]()
Точкой локального
экстремума называют
точку непрерывности функции
![]() ,
в окрестности которой приращение функции
сохраняет знак:
,
в окрестности которой приращение функции
сохраняет знак:![]() -
точка локального минимума,
-
точка локального минимума,![]() -
точка локального максимума. Необходимые
условия существования экстремума
записываются следующим образом:
-
точка локального максимума. Необходимые
условия существования экстремума
записываются следующим образом:
![]() ,
,
что равносильно системе уравнений для нахождения критических точек функции:
 или
или
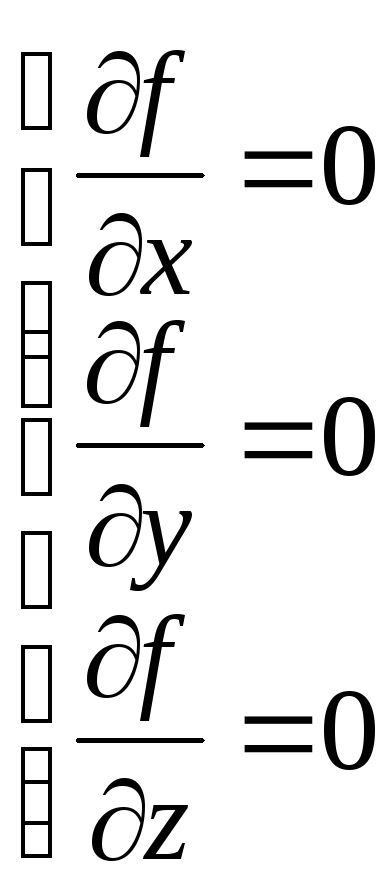 .
.
Достаточные условия существования экстремума определяются знаком приращения функции, который в свою очередь определяется знаком второго дифференциала:
![]() ,
то точка
,
то точка
![]() является точкой локального минимума,
является точкой локального минимума,
![]() ,
то точка
,
то точка
![]() является точкой локального максимума.
является точкой локального максимума.
По
своей структуре второй дифференциал
является является квадратичной формой
относительно дифференциалов
![]() и ему ставится в соответствие матрица:
и ему ставится в соответствие матрица:
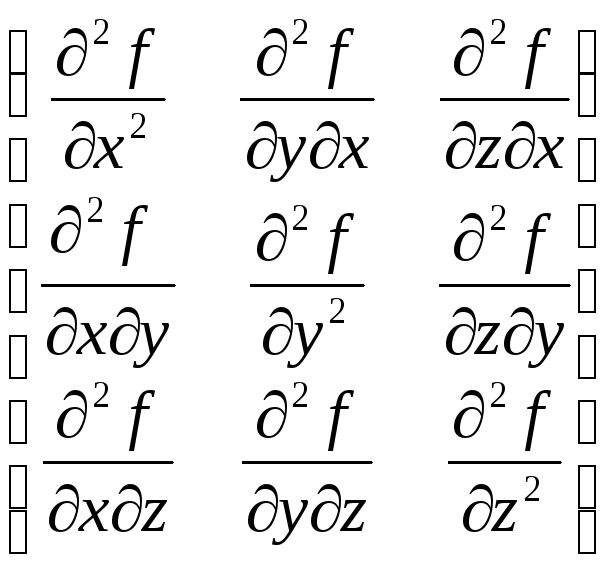 .
.
Согласно критерию Сильвестра квадратичная форма является положительно определенной, если положительны все главные диагональные миноры этой матрицы:
![]() ,
,
![]()
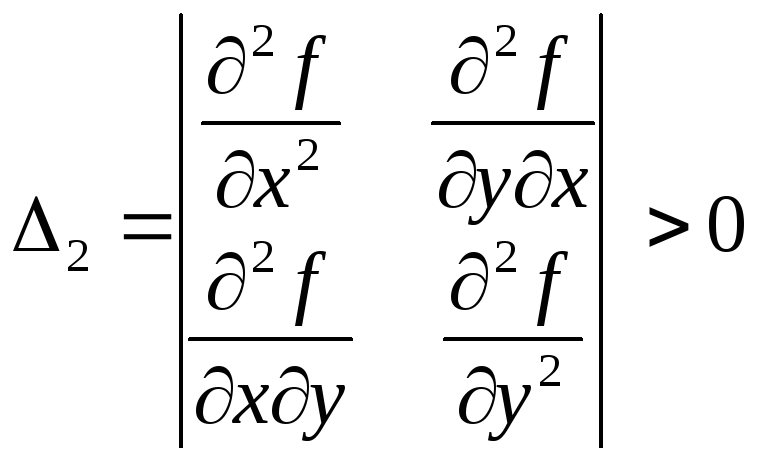 ,
,
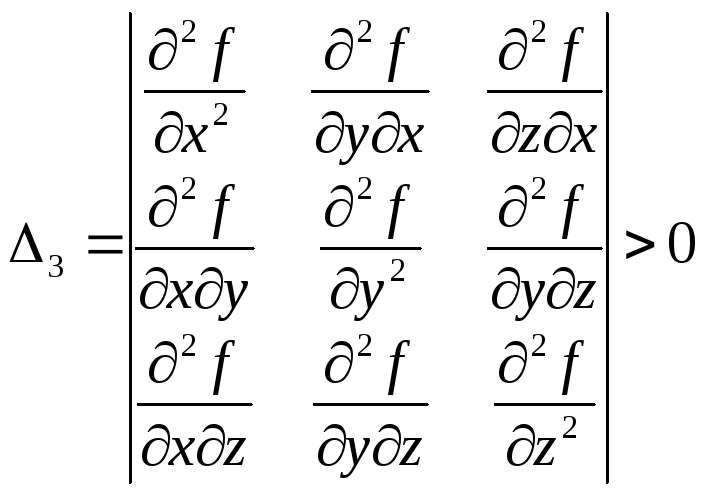 .
.
(условия
существования локального минимума), и
является отрицательно определенной
при условии
![]() ( условия существования локального
максимума).
( условия существования локального
максимума).
Для нахождения точек условного экстремума исследуют на обычный экстремум функцию Лагранжа
![]()
![]() .
.
Здесь
![]() - условие связи, а
- условие связи, а![]() - множитель Лагранжа. При этом достаточные
условия существования экстремума
выражаются через знак второго дифференциала
- множитель Лагранжа. При этом достаточные
условия существования экстремума
выражаются через знак второго дифференциала![]() (условие
минимума),
(условие
минимума),![]() -
условие максимума. Знак второго
дифференциала можно анализировать
непосредственно при наличии условий
связи.
-
условие максимума. Знак второго
дифференциала можно анализировать
непосредственно при наличии условий
связи.
Задачи
Запишите производные второго порядка для указанной функции, в указанной точке.
Запишите второй дифференциал.
Запишите матрицу, соответствующую d2f.
Запишите разложение по формуле Тейлора в указанной точке:
а)
![]()
б)
![]()
Исследуйте функцию на локальный экстремум:
-
а)

б)

в)

На эллипсоиде Х2+2У2+4Z2=8 найти точку, наиболее удалённую от М0(0;0;3).
Метод наименьших квадратов.
По точкам, полученным в некотором эксперименте, требуется провести прямую линию таким образом, чтобы сумма квадратов отклонений экспериментальных точек от предполагаемой прямой была наименьшей.
у=Ах+В – искомая функция;
А,В – искомые коэффициенты.
Функция
![]() должна достигать минимума при выбранных
А,В.
должна достигать минимума при выбранных
А,В.
Исследуйте функцию S(A,B) на локальный экстремум.
Получите выражение для А, В, соответствующие экстремуму.
Постройте по методу наименьших квадратов прямую по точкам:
|
Хi |
Уi |
|
2 |
2 |
|
4 |
2 |
|
6 |
5 |
|
7 |
4 |
|
9 |
8 |
|
Контрольные вопросы
по направлению. Какова взаимосвязь между ними?
градиентом и производной по направлению?
функции в этом направлении?
функции двух и трех переменных
Ответы: Задача 2. а)(-1;1) – максимум; (1;-1) – минимум; б)(-3;2;-1) – максимум; в)(2; -6; 1) – минимум; |
|
Задача 3. Х0;=-1; М1(2;0;-1); М2(-2;0;-1);d2L0;
|
|
Задача 4 и примечания к ней
У=0,8Х–0,4;
|
|
Записываем необходимые условия существования экстремума для функции
двух переменных
В результате для нахождения оценок получаем систему уравнений:
решение которой имеет вид :
|
|
|
Уi |
|
|
2 |
2 |
|
|
4 |
2 |
|
|
6 |
5 |
|
|
7 |
4 |
|
|
9 |
8 |
|
|
| ||
|
| ||
|
| ||
|
| ||

 равна…
равна…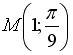 равна…
равна… ,
,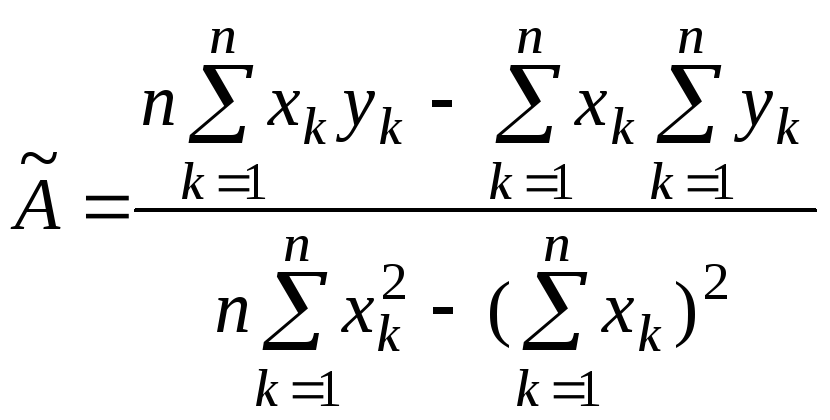 ,
,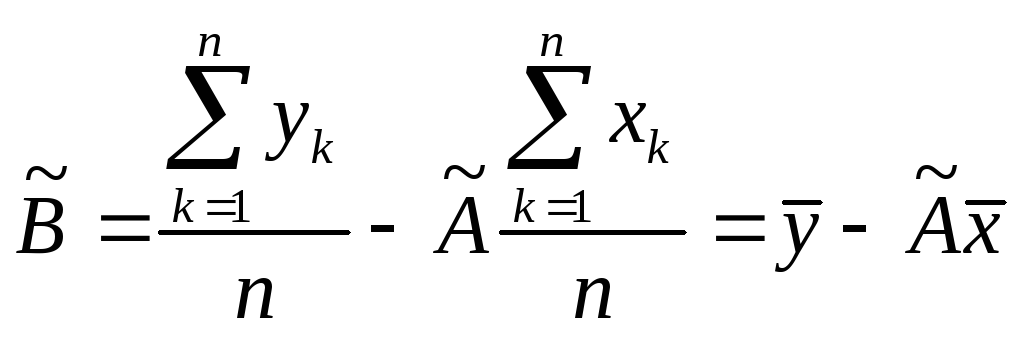 .
.