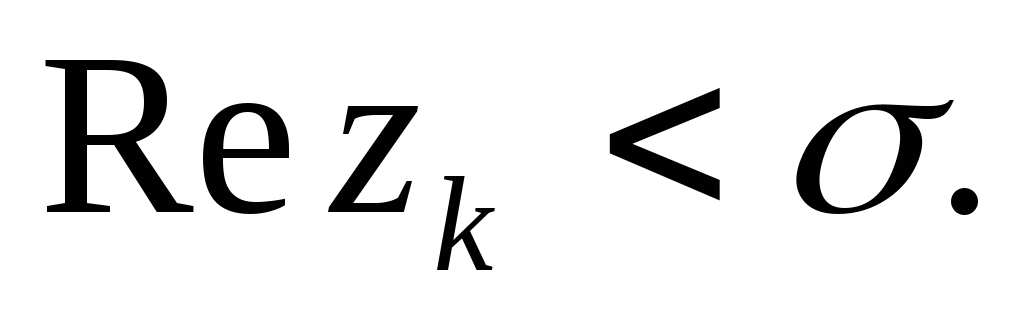Литература.
1. Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного переменного. М.: Наука, 1987. 684 с.
2. Сидоров Ю. В., Федюк М. В., Шабунин М. И. Лекции по теории функций комплексного переменного. М.: Наука, 1989. 477 с.
3. Сиберт У. М. Цепи, сигналы, системы (части 1,2). М.: Мир, 1988. 358 с.
Приложение.
ВЫЧЕТ АНАЛИТИЧЕСКОЙ ФУНКЦИИ В ОСОБОЙ ТОЧ-КЕ. ПРИМЕНЕНИЕ К ВЫЧИСЛЕНИЮ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ
Точка
z
= z
,
лежащая в конечной части комплексной
плоскости, является изолированной
особой точкой типа полюс для функции
f(z),
если функцию в окрестности z=z
можно представить в виде f(z)
=
m
- порядок полюса, 
.
Вычетом
функции f(z)
в точке z
= z
называют
коэффициент C
разложения f(z)
в ряд Лорана:
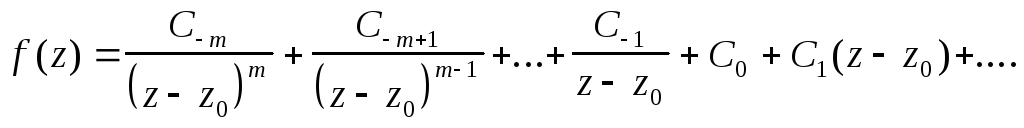
Вычет в особой точке-полюс можно вычислить по формуле
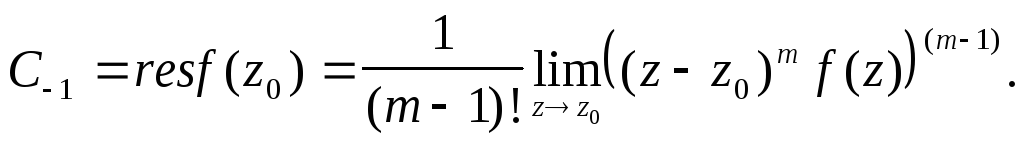
Кроме того, для случая m=1 можно использовать формулу
res
f(z
)
=
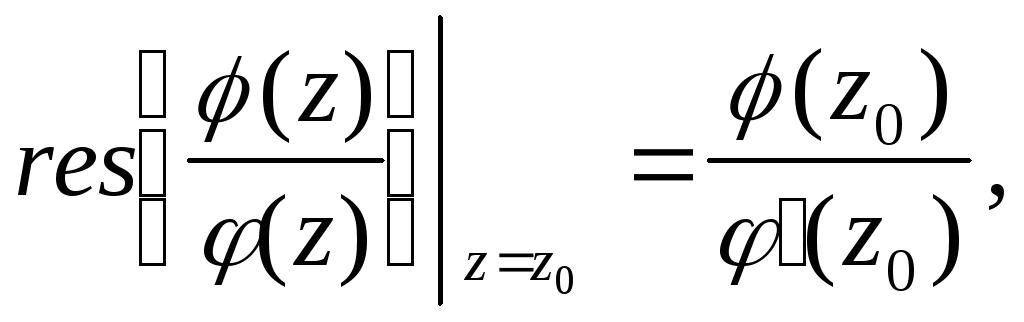
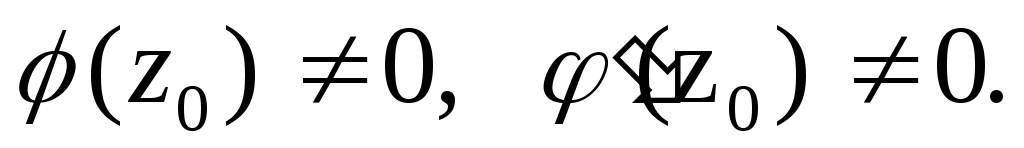
Если при решении задачи необходимо найти сумму вычетов в комплексно-сопряженных точках, то удобно использовать следующую формулу:
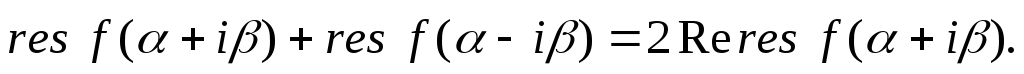
Для вычисления несобственных интегралов можно использовать формулы:
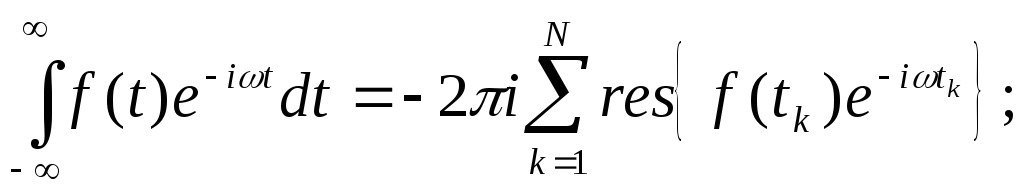
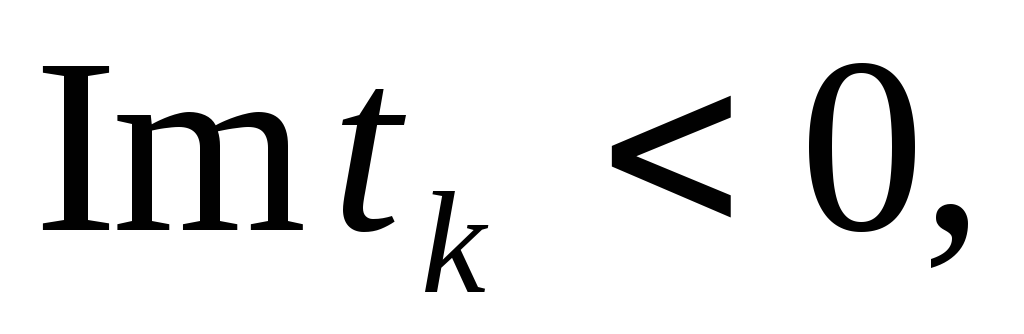
при
t.
.
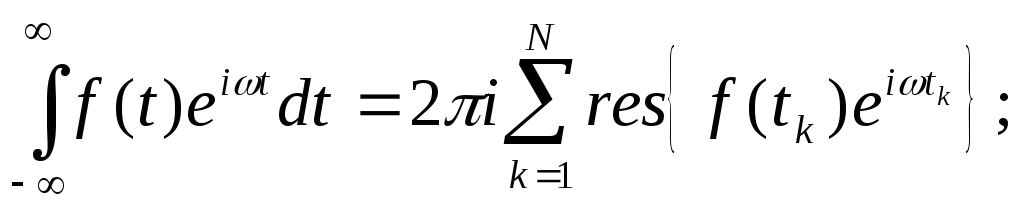
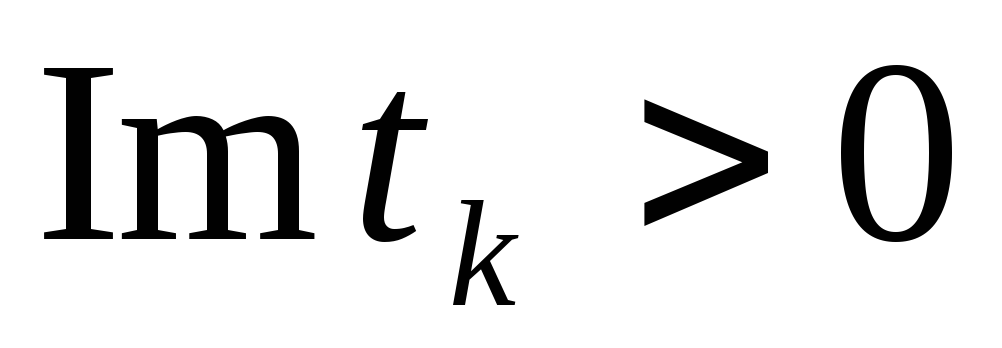