Предисловие.
Пособие
посвящено специальным и практически
важным для подготовки инженеров разделам
курса высшей математики: ряды и
преобразования Фурье, интегральные и
дискретные преобразования Лапласа (
-
преобразования). Методы решения линейных
дифференциальных уравнений и систем
уравнений, основанные на этих
преобразованиях, находят широкое
применение, например, в электротехнике,
теории автоматического управления,
теории надежности.
Уровень строгости изложения сориентирован на студентов второго курса технического вуза и предполагает знакомство с основами теории функций комплексного переменного, особенно с теорией вычетов.
Поскольку пособие рассчитано на организацию самостоятельной работы студентов, оно содержит кроме теоретического материала большое количество подробно разработанных задач, демонстрирующих технику конкретных вычислений, а также задания для выполнения самостоятельной работы и ответы к ним.
1. ТРИГОНОМЕТРИЧЕСКИЕ РЯДЫ ФУРЬЕ
1.1 ПОНЯТИЕ О ГАРМОНИЧЕСКОМ (СПЕКТРАЛЬНОМ) АНАЛИЗЕ
Колебательные движения играют большую роль в самых различных областях техники (механика, теория упругости, электротехника). Простейшим периодическим движением является гармоническое колебание, которое математически задается функцией
где
амплитуда колебания 
,
-
начальная фаза,
-
минимальный период функции: 
-
общий период функции 
,
- частота колебания (гармоники),
=
─
циклическая
частота.
Заметим
что функция 
как и
определяет
гармоническое колебание с тем же
периодом:
характеристики которого однозначно определяются из соотношений:
Конечная
сумма гармонических колебаний с периодом
задает сложное колебательное движение:
И,
наконец , еще более сложное колебательное
движение (
)
можно представить как сумму сходящегося
для всех t
ряда:
который
называется тригонометрическим рядом.
Числа
,
называют коэффициентами тригонометрического
ряда, а члены ряда
-гармониками,
соответствующими частоте
.
Отметим, что в физике представление сложного периодического движения как суммы (конечной или бесконечной) простых гармонических колебаний одного периода широко распространено. При этом выделение из сложного периодического движения составляющих его гармонических колебаний имеет большое практическое и теоретическое значение, в различных областях физики и техники для этой цели существуют специальные приборы (резонаторы, спектрометры). Дискретным частотным спектром периодической функции называют полученный при помощи этих приборов набор гармонических колебаний, который формирует сложный сигнал. В математике выделение гармонических составляющих делают, разлагая функцию в тригонометрический ряд, что и составляет основную задачу теории тригонометрических рядов Фурье.
1.2 ОРТОГОНАЛЬНОСТЬ ОСНОВНОЙ СИСТЕМЫ
ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ.
КОЭФФИЦИЕНТЫ ФУРЬЕ
Систему
функций 
непрерывных на
называют ортогональной на этом интервале,
если для скалярного произведения функций
справедливо
при
всех 
.
Если при этом выполняется условие:
то
систему функций называют ортонормированной,
а число 
называют нормой.
Покажем,
что данному определению ортогональности
на интервале (
)
удовлетворяет основная система
тригонометрических функций:
Для этого вычислим интегралы:
(1.1)
так
как при 
,
и
-
целые числа.
как интеграл от нечетной функции на симметричном интервале.
Вычислим
также нормы функций. При
имеем
и
(1.2)
а
при 
получаем:
(1.3)
(1.3)
Аналогично
(1.4)
Таким образом, система функций
(1.5)
является
ортонормированной на (
).
При
условии
ортонормированная система функций
принимает простой вид:
(1.6)
Можно
сказать, что система функций является
базисом бесконечной размерности в
линейном пространстве функций, которые
являются периодическими с периодом 
.
Поэтому периодическая функция, заданная
на (
),
мо-жет быть представлена в виде линейной
комбинации с коэффициентами 
:
(1.7)
Предположим, что тригонометрический ряд (1.7) сходится и допускает почленное интегрирование. Интегрируя почленно ряд (1.7), имеем:
так
как
,
как интеграл от нечетной функции на симметричном интервале. В результате этих вычислений получаем, что
(1.8)
.
Заметим,
что при этом первый член (1.7)
имеет смысл среднего значения
на интервале (
).
Умножая
ряд (1.7) на 
и выполняя почленное интегрирование,
получаем:
(1.9)
При вычислении интеграла использовали свойство ортогональности (1.1) и нормы (1.4).
Из (1.9) следует, что
.
(1.10).
Аналогично,
умножая обе части ряда (1.7) на 
и почленно интегрируя, имеем
.
(1.11)
Коэффициенты (1.8), (1.10), (1.11) называют коэффициентами Фурье.
Определение.
Тригонометрический
ряд (1.7), коэффициенты которого являются
коэффициентами Фурье, называют рядом
Фурье
периодической функции, заданной на
симметричном интервале (
).
При
условии 
коэффициенты и ряд Фурье имеют простой
вид:
П
y
)
(рис. 1.1)
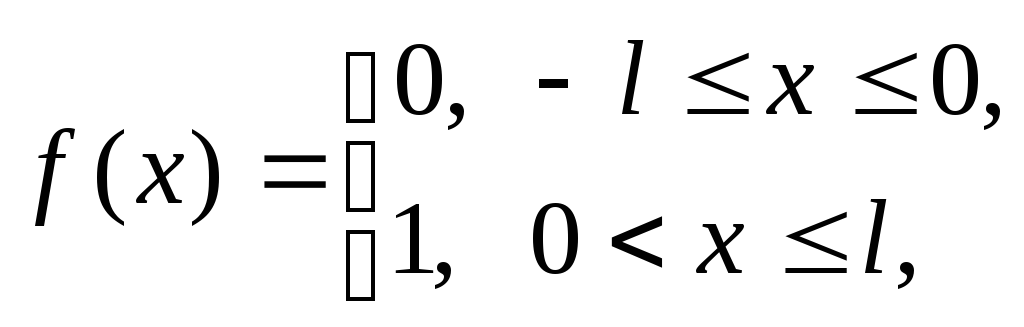
в ряд Фурье по тригонометрическим функциям.
Рис.
1.1
Замечая,
что период
равен
,
вычисляем коэффициенты Фурье:
с
учетом того, что 
В результате получаем, что разложение данной функции в ряд Фурье имеет вид:
По
известному разложению в ряд Фурье легко
построить дискретный
частотный
спектр
периодической функции, который наглядно
показывает вклад каждой из гармоник в
сложное колебательное движение. Для
этого строят диаграмму в координатах
,
где
-
номер гармоники,
- амплитуда.
Для
рассматриваемой функции
спектр имеет вид (рис. 1.2):
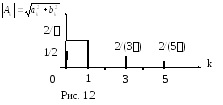
Учитывая четность подынтегральных функций, можно установить особенности разложения в ряд Фурье для четных и нечетных функций.
Так,
если функция
-
четная,
получаем:
=0
и разложение в ряд имеет вид :
(1.7a)
Если
-
нечетная,
справедливо:
и разложение в ряд имеет вид:
(1.7б)
Пример 1.2. Разложить в ряд Фурье по синусам функцию, заданную на полуинтервале:
Рис.
1.3
,
нужно
вычислить только коэффициенты b
:
=
=
=-
........
Обобщая полученный результат, получаем:
.
1.3 ДОСТАТОЧНЫЕ УСЛОВИЯ СХОДИМОСТИ РЯДА ФУРЬЕ
Если
функция 
с
периодом 
и ее производная 
,
определенные на интервале 
являются на отрезке [
]
непрерывными или кусочно-непрерывными
(имеют на заданном отрезке конечное
число точек разрыва первого рода и
конечное число экстремумов), тогда
справедливо:
1)
ряд Фурье функции
сходится
к самой функции для всех
и сумма ряда
равна
в точках непрерывности
;в точках разрыва
где
для непрерывной
сходимость
ряда является равномерной.
Таким
образом, любая кусочно-непрерывная
функция, заданная на интервале (
),
может быть периодически с периодом
продолжена
на всю действительную ось и разложена
в ряд Фурье. В том случае, если функция
у
y
дов
),
ее можно разложить в ряд Фурье
различными способами в зависимости от
характера периодического продолжения.
Так, при четном продолжении на (
,
0) функцию f(x)
можно разложить в ряд по косинусам
(1.7a)
(рис.1.4), а при нечетном продолжении - в
ряд по синусам (1.7б)
(
Рис.
1.5 y
y
рис.
1.5).
эти требования не предъявляются)
справедливо:
(1.8)
Путем
непосредственного вычисления интеграла
(1.8) с учетом свойств ортогональности
(1.1) можно получить равенство
Парсеваля,
которое задает средний квадрат функции
f(x)
на интервале (
)
:
(1.9)
Если
переменная
имеет
смысл времени, то
величина
есть средняя
мощность
временного сигнала . Тогда равенство
Парсеваля утверждает следующее: средняя
мощность сигнала равна сумме мощностей
его гармоник.
Покажем, как использовать равенство Парсеваля для нахождения суммы числового ряда.
Пример
1.3. Найти
сумму числового ряда 
Для
решения задачи найдем коэффициенты
Фурье для функции 
при продолжении на интервал 
нечетным образом (рис.1.6):
Теперь используя равенство (1.9), получим:
Рис. 1.6
1.4 РЯД ФУРЬЕ В КОМПЛЕКСНОЙ ФОРМЕ
Для того, чтобы переписать ряд Фурье
в
комплексной форме, выразим входящие в
формулу функции
и
через экспоненты с мнимым показателем:
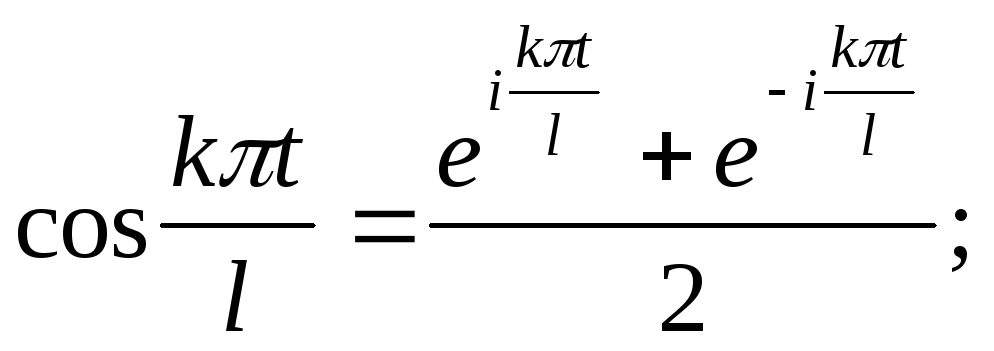
Тогда разложение функции в ряд будет иметь вид:
Вводя
обозначения
=
=
=
,
получим ряд Фурье в комплексной форме:
Используя
выражения для действительных коэффициентов
и формулу Эйлера, запишем выражения для
коэффициентов 
и 
:
Поскольку
является комплексным числом, его можно
записать в тригонометрическом и
показательном виде:
где
модуль и аргумент
имеют вид:
;
Отметим,
что для действительных функций f(t)
справедливо: 
,
(
- комплексно-сопряженное число с
);
= 
.
Спектральной
плотностью
называют отношение коэффициента c
ряда Фурье к приращению частоты
:
=
=
Амплитудным
спектром
называют модуль спектральной плотности
,
а фазовым
спектром
-
взятый с обратным знаком аргумент
спектральной плотности
Пример 1.4. Найти разложение в ряд Фурье в комплексной форме периодического прямоугольного импульса, который на основном периоде задается выражением (рис. 1.7)
=
Для коэффициента Фурье
и
Рис.
1.7
Рис.
1.8
Для спектральной плотности получаем:
.
Амплитудный
спектр 
можно построить, задавая номера гармоник:
и
нанося их на диаграмму (
;
).
При этом получим дискретный (линейчатый)
спектр (рис. 1.8)
Следствием
условия 
= 
является то, что спектральная плотность
S(
)
симметрична относительно оси ординат.
Аналогично
вычисляя -
для
различных гармоник,получим фазовый
спектр
(рис. 1.9).
2. ПРЕОБРАЗОВАНИЯ ФУРЬЕ
2.1 ИНТЕГРАЛ ФУРЬЕ
Рассмотрим
функцию
,
удовлетворяющую следующим условиям:
1)
определены на интервале 
являются непрерывными или кусочно-непрерывными
(могут иметь конечное число точек разрыва
1-ого рода);
2)
является абсолютно интегрируемой, то
есть несобственный интеграл 
сходится.
Функция
f(t)
не является периодической, но на любом
конечном симметричном интервале (
)
может быть представлена рядом Фурье:
Вводя
перепишем разложение f(t)
в следующем виде:
Переходя
к пределу при условии 
получим представление функции f(t)
несобственным интегралом, который
называют интегралом
Фурье:
Вводя специальное обозначение для внутреннего интеграла:
(2.1)
перепишем интеграл Фурье в виде:
(2.2)
Соотношения
(2.1) и (2.2) называют
прямым и
обратным
преобразованиями
Фурье
соответственно. Прямое преобразование
Фурье
называют
такжеспектральной
плотностью.
Эта функция дает анализ частотного
состава временного сигнала
.
В отличие от спектральной плотности
периодической функции функция
является
непрерывной и служит огибающей для
соответствующего дискретного спектра.
Пример 2.1. Найти спектральную плотность одиночного прямоугольного импульса (рис. 2.1):
Г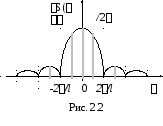
рафик
функцииS(
огибает дискретный спектр частот
прямоугольного периодического импульса
(рис. 2.2):
2.2 КОСИНУС- И СИНУС-ПРЕОБРАЗОВАНИЯ ФУРЬЕ
В общем случае спектральная плотность S() является функцией комплексного переменного:
S() = U() + iV();
Если функция f(t) является четной, то мнимая часть V()=0 (как интеграл от нечетной функции на симметричном интервале). Спектральная плотность в этом случае имеет вид:
Полученное преобразование называют косинус-преобразованием Фурье.
Если функция f(t) является нечетной, то вещественная часть U()=0 и спектральная плотность имеет вид:
которое называют синус-преобразованием Фурье.
Обратные преобразования задаются следующими соотношениями:
Рассмотрим примеры нахождения прямых и обратных преобразований Фурье.
Пример
2.2. f(t)
=
При
вычислении интеграла использовали
соотношение
при t
.
Н
аходим
спектральные характери стики функции:
1) амплитудный спектр
(рис. 2.3):
2) фазовый спектр (рис. 2.4)
.
.
Пример
2.3.
В силу четности функции находим косинус-преобразование
Фурье:
Пример 2.4. График функции представлен на рис. 2.5:
В силу четности функции находим косинус-преобразование Фурье:
Постройте график этой функции самостоятельно.
Пример
2.5.
Поскольку функция является нечетной, то находим синус-преобразование Фурье:
Так
как
при 
для вычисления интеграла можно
использовать теорему о вычетах:
Таким образом, учитывая, что подынтегральная функция имеет полюс второго порядка в нижней полуплоскости, спектральная плотность запишется в следующем виде:
Пример 2.6. Найти преобразование Фурье для функции Гаусса
(рис. 2.6)
.
Для вычисления спектральной плотности
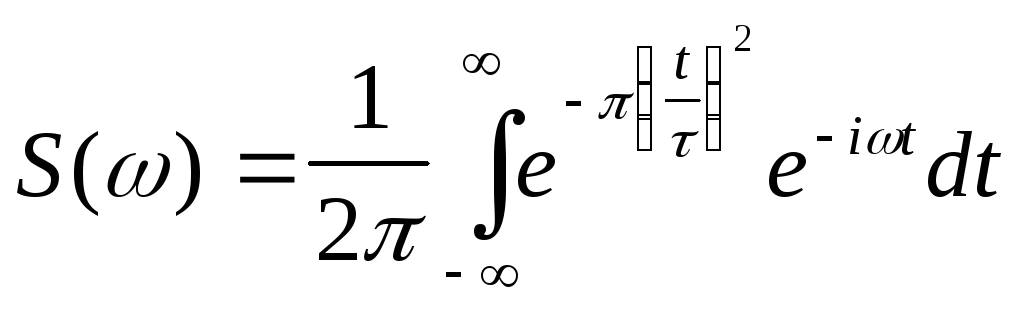
покажем
предварительно, что интеграл Пуассона
Действительно, вычисляя квадрат интеграла в полярной системе координат, получаем:
Далее сведем вычисление интеграла Фурье к интегралу Пуассона:
Здесь ввели при вычислении интеграла переменную
График S() изображен на рис. 2.7.
Покажем, как при заданной спектральной плотности восстановить функцию f(t), то есть найти обратное преобразование Фурье.
Пример
2.7. По
известной спектральной плотности 
найти обратное
преобразование Фурье.
Для
вычисления интеграла используем теорему
о вычетах, записанную через переменную
с учетом того, что подынтегральная
функция имеет простой полюс в верхней
полуплоскости 
при
.
2.3 НЕКОТОРЫЕ СВОЙСТВА ПРЕОБРАЗОВАНИЙ ФУРЬЕ
Рассмотрим основные свойства преобразований Фурье.
1. Линейность.
Пусть
функции
и
имеют своим преобразованием Фурье
функции
и
соответственно.
Тогда для функции
преобразованием Фурье служит функция
.
Это свойство следует непосредственно из свойств определенного интеграла, которым и является преобразование Фурье.
2. Симметрия.
Если
-
преобразование Фурье для функции
,
то
является
преобразованием Фурье для функции
.
Рассмотрим это на примерах.
П
Преобразованием
Фурье для функции
является функция
=
Легко проверить, что преобразованием
Фурье для функции
=
является функция
(рис. 2.8).
Рис.
2.8
Пример
2.9.
=
=
3. Дифференцирование.
Если
S()
является преобразованием Фурье для
функции f(t),
то для производной f(t)
преобразованием Фурье будет функция
:
.
Действительно, интегрируя по частям,
имеем:
при
условии, что
при
и
.
4. Преобразование свертки.
Преобразованием
Фурье свертки двух функций
и
является произведение их преобразований
Фурье:
Преобразование произведения.
Преобразование Фурье произведения двух функций g(t)f(t) является сверткой их преобразований Фурье:
Теорема Парсеваля.
Из
свойства 5 следует: 
Интеграл
называют полной энергией временного
сигнала
,
а 
-
энергетическим спектром. Тогда согласно
теореме Парсеваля полная
энергия
равна сумме
энергий всех его частотных составляющих.
Класс
абсолютно интегрируемых функций, для
которых можно непосредственно найти
преобразование Фурье, достаточно узок.
Так, не являются абсолютно интегрируемыми
функции
единичная ступенчатая функция Хевисайда
Для записи преобразований Фурье таких
функций используют импульсную
дельта-функцию Дирака (
-функцию).
ИМПУЛЬСНАЯ ДЕЛЬТА-ФУНКЦИЯ ДИРАКА
Дельта-функция Дирака, исторически названная -функцией, не является функцией в обычном смысле этого понятия. Значение этой функции в точке смысла не имеет, функция не задается какой-либо определенной формулой и не может быть вычислена каким-либо способом, а определяется только действием, которое она производит. Такие функции называют обобщенными функциями или функционалами.
Определяющим свойством импульсной -функции является следующее: свертка импульсной функции с любой функцией воспроизводит саму эту функцию. Данное свойство записывается в виде интеграла свертки:
a
t
b 
Использование
импульсной функции в интеграле
позволяет выбрать значение подынтегрального
выражения в точке, характеризуемой
наличием в ней единичного импульса
(рис. 2.10). Для бесконечного интервала
интегрирования свертка с импульсом
записывается следующим образом:
Приведем
также интеграл свертки с производной
-функции:
Действительно,
выполнив свертку
и
,
получим:
Дельта-функцию можно истолковать как предельный физический процесс (импульсное воздействие), в котором рассматривается бесконечно большая величина (например, сила), действующая в бесконечно малый промежуток времени с суммарным эффектом, равным единице. Формально это утверждение можно записать в виде условий:
Дельта-функция может быть смоделирована при помощи предельного перехода любой функции, ведущей себя неограниченно в окрестности нуля. Приведем примеры:
1
)
(рис. 2.11).
Рис.
2.12
Исследуем
связь между
импульсной функцией и единичной функцией
Хевисайда
Запишем интеграл свертки ступенчатой и импульсной функций:
поскольку
(рис. 2.13).
Рис.
2.13
Таким
образом, интеграл от единичной импульсной
функции является единичной ступенчатой
функцией. Следовательно производной
от единичной ступенчатой функции можно
считать импульсную функцию: 
Покажем,
что производная
в
интеграле свертки выполняет ту же роль,
что и
:
Таким образом, справедливы соотношения:
;
2.5 ПРЕОБРАЗОВАНИЕ ФУРЬЕ НЕАБСОЛЮТНО ИНТЕГРИРУЕМЫХ ФУНКЦИЙ
Используя
результаты предыдущего параграфа,
найдем преобразование Фурье для
-
функции (рис. 2.14):
Рис.
2.14
Согласно
свойству симметрии преобразований
Фурье получаем преобразование Фурье
для постоянной
(рис.
2.15):
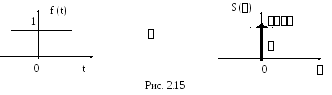
Отметим,
что длительность сигнала
и ширина спектра
связаны соотношением:
.
Для
смещенных импульсных функций
,
преобразования Фурье имеют вид:
Используя далее свойства линейности и симметрии преобразований , можно записать следующие соотношения:
,
В
заключение найдем спектральную плотность
ступенчатой функции Хевисайда. Для
этого рассмотрим вспомогательную
функцию
,
которая при условии
стремится к t.
В результате получаем, что
3. ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
3.1 ОРИГИНАЛ И ИЗОБРАЖЕНИЕ ПО ЛАПЛАСУ. УСЛОВИЯ СУЩЕСТВОВАНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
Преобразованием
Лапласа для функции 
называется функция
где
- комплексная переменная. Функция 
является комплексной функцией
действительного аргумента и называется
функцией-оригиналом. Эта функция обладает
следующими свойствами:
1)
для всех
;
интегрируема
на любом конечном интервале;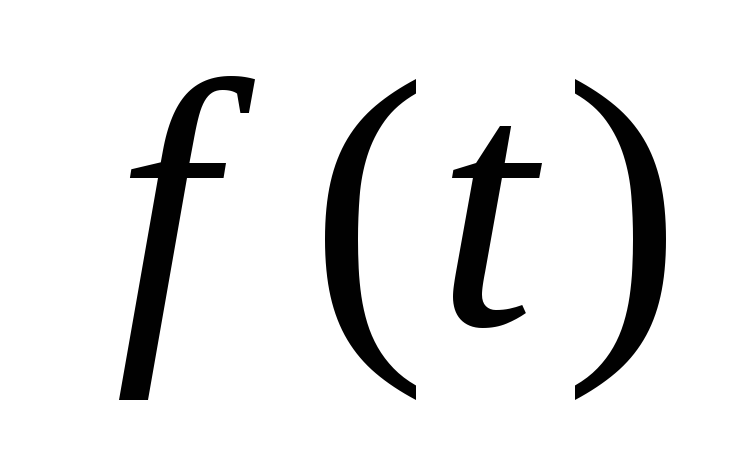 
возрастает
не быстрее некоторой показательной
функции , то есть существуют такие 
и 
,
что для всех t
справедливо
.
Число
называют показателем роста функции 
.
При этих условиях несобственный
интеграл сходится абсолютно:
.
Данные условия выполняются для большинства функций, описывающих физические процессы. При этом момент начала наблюдения над процессом всегда можно принять равным нулю, а всю информацию до момента начала наблюдения включить в начальные условия задачи.
Простейшей функцией-оригиналом является единичная функция Хевисайда
При
умножении на единичную функцию любая
функция
,
удовлетворяющая только второму и
третьему условиям, может быть преобразована
в функцию, удовлетворяющую также и
первому условию :
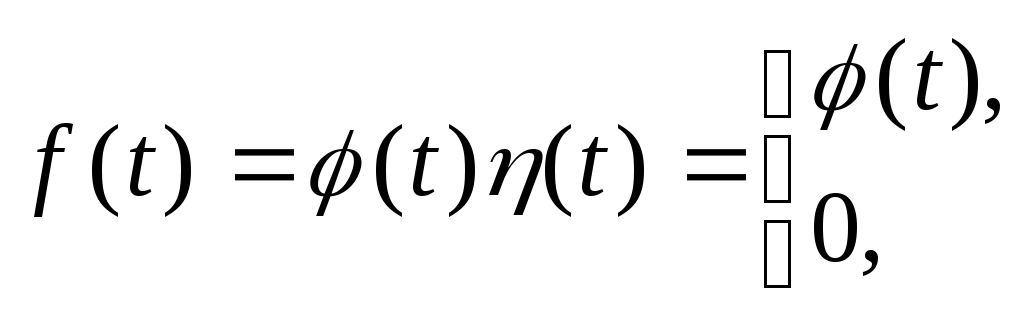
Для
обозначения соответствия функции-оригинала
ее изображению по Лапласу введем знак
:
Cправедлива
теорема:
для всякого оригинала 
изображение по Лапласу 
определено
в полуплоскости 
и является в этой полуплоскости
аналитической функцией, то есть 
при условии 
равномерно относительно аргумента 
и имеет конечную производную.
Действительно, с учетом того, что
получается оценка :
Аналогично
получается оценка производной : 
Рассмотрим примеры нахождения преобразований Лапласа для простейших функций :
Пример
3.1. 
Пример
3.2. 
Пример
3.3. 
Пример
3.4. 
3.2 СООТВЕТСТВИЕ МЕЖДУ ПРЕОБРАЗОВАНИЯМИ ФУРЬЕ И ПРЕОБРАЗОВАНИЯМИ ЛАПЛАСА
Сравнение преобразований Фурье и Лапласа и условий их существования:
показывает,
что преобразование Фурье существует
для более узкого, чем преобразования
Лапласа, класса функций. Требование
абсолютной интегрируемости f(t)
для существования преобразований Фурье
не позволяет непосредственно выразить
спектральную плотность таких важных
функций как (t),
cos
t,
sin
t,
e
.
В то же время преобразование Лапласа
для этих функций существует. Это
обеспечивается наличием под знаком
интеграла множителя e
.
Но если f(t)
= 0 при t
< 0 и преобразование Фурье для f(t)
существует (f(t)
абсолютно интегрируема), то оно может
быть получено из преобразований Лапласа
заменой переменной p
= i:
S()
= F(i).
3.3 СВОЙСТВА ПРЕОБРАЗОВАНИЙ ЛАПЛАСА.
3.3.1 Линейность .
Линейность преобразований Лапласа следует из свойств интегралов.
Пусть
Тогда
На основании этого свойства легко получить преобразования Лапласа для более сложных функций, например для sin t:
Аналогично доказываются соотношения:
3.3.2 Подобие.
Для
любого постоянного
справедливо
Действительно,
3.3.3 Дифференцирование оригинала.
Если
непрерывна при 
,
а
являются
оригиналами, то справедливы соотношения:
Действительно, интегрируя по частям, можно получить эти соотношения из определения преобразований Лапласа.
Например,
Здесь
использовалась оценка: 
Примечание. Если функция имеет точки разрыва первого рода на интервале интегрирования, например функция, представленная на рис. 3.1:
g(t)
то преобразование Лапласа для производной будет определяться соотношением
3.3.4 Дифференцирование изображения.
Дифференцирование
изображения сводится к умножению
оригинала на 
.
Результат получается дифференцированием
по параметру 
:
Переходя к другим обозначениям, получаем:
Пример
3.5. Основываясь
на известном соотношении 
получить преобразование Лапласа для
f(t)
= t
sint:
Используя дифференцирование изображения, доказать соотношения:
3.3.5 Интегрирование оригинала.
Интегрирование
оригинала сводится к делению изображения
на 
при условии, что функция-оригинал 
непрерывна:
Действительно,
вводя функцию 
такую, что
, с учетом того, что 
и переходя к изображениям, получаем
и
Замечание. Если функция-оригинал на интервале интегрирования имеет точки разрыва первого рода, например функция, представленная на рис. 3.2:
то
учитывая, что 
получаем
3.3.6 Интегрирование изображения.
Если
сходится, то справедливо соотношение:
Действительно,
в области 
имеем:
Рассмотрим применение свойств интегрирования оригинала и изображения для нахождения преобразования Лапласа.
Пример 3.6. Найти изображение по Лапласу функции
Решение проводим в 3 действия:
1) используя свойство линейности и таблицу, находим
используя свойство интегрирования изображения, находим
используя свойство интегрирования оригинала, получаем:
3.3.7 Смещение изображения.
Для
любого комплексного
справедливо:
Действительно,
Следующие соотношения доказываются с учетом последнего свойства:
Соотношения:
доказываются с использованием свойств линейности и смещения изображения.
Применение свойства смещения изображения позволяет найти оригинал по изображению.
Пример 3.7. Найти оригинал по заданному изображению:
3.3.8 Запаздывание оригинала.
Для
любого 
справедливо
то есть умножение изображения на экспоненту с показателем (-) равносильно смещению оригинала на (рис. 3.3). Действительно:
Пример
3.8. Найти
изображение по оригиналу 
,
используя свойство запаздывания
оригинала.
.
Пример 3.9. Найти изображение по оригиналу функции
(рис. 3.4), задающей прямоугольный импульс:
Рис.
3.4
Предварительно представив функцию t через ступенчатые функции (t) и (t-), получим изображение:
.
Пример
3.10. Найти
изображение импульсной
функции
Дирака. Представив 
функцию
как предел отношения:
получим
преобразование Лапласа 
Для
абсолютно интегрируемых функций по
изображению по Лапласу легко получить
выражение для преобразования Фурье
заменой 
.
Пример 3.11. Найти преобразование Фурье функции, задающей прямоугольный импульс, рассмотренный в примере 3.9.
.
Пример 3.12. Рассмотрим несколько способов нахождения преобразований Лапласа для функции, изображенной на рис. 3.5:
Способ 1. Непосредственное вычисление интеграла:
Способ 2. Записать функцию через единичные функции и воспользоваться теоремой запаздывания :
Способ 3. Записав производную через единичные функции, с учетом граничных условий найдем изображение, а затем применим свойство интегрирование оригинала :
3.3.9 Преобразования Лапласа периодических функций.
Для
периодической функции-оригинала с
периодом
:
построим вспомогательную функцию:
Тогда преобразование Лапласа для этой вспомогательной функции с учетом свойства запаздывания имеет вид:
Для основной функции получаем соотношение:
Пример 3.13. Найти преобразование Лапласа для периодически повторяющегося сигнала в виде прямоугольных импульсов, заданного функцией (рис. 3.6):
Пример 3.14. Найти преобразование Лапласа сигнала периодических треугольных импульсов, заданных на основном периоде функцией (рис. 3.7):
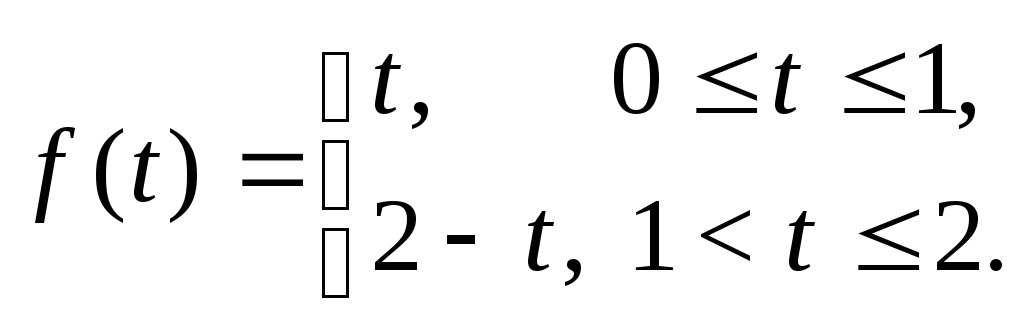
t
Предварительно удобно найти изображение производной (рис. 3.8):
Рис.
3.8
3.3.10 Умножение изображений (изображениe свертки).
Сверткой функций f(t) и g(t) называется функция, которая обозначается fg и определяется равенством
Свертка (fg)(t) = f(t)g(t) является оригиналом. Найдем изображение этой функции:
Поскольку двойной интеграл сходится абсолютно в области
Re
p
,
то изменяя порядок интегрирования (рис.
3.9), получаем:
.
Таким образом, произведению изображений соответствует свертка оригиналов:
f(t)F(p), g(t)G(p).
Cледствием этой теоремы является интеграл Дюамеля:
pF(p)G(p)
LpF(p)G(p)
= f(0)g (t) +
=
=
f(0)g(t)
+
=
f(t)g(0)
+
=
=
f(t)g(0)
+
.
Действительно,
pF(p)G(p) - f(0)G(p) + f(0)G(p) = G(p)(pF(p) - f(0)) + f(0)G(p)
f(0)g(t)
+
= f(0)g(t)
+
.
Рассмотрим примеры на использование этого свойства.
Пример
3.15. Найти
изображение оригинала: 
.
Здесь
f(t)
= t
,
g(t)
= cos
2t.
Поэтому F(p)
=
или Lt
=
;
G(p)
=
или
Lcos
2t
=
;
L
=
.
Полученное свойство оригиналов и изображений может быть использовано для нахождения оригиналов по их изображениям.
Пример 3.16 Показать справедливость соотношения:
L
=
(sin
t - t cos t)
или
(sin
t - t cos t) .
Здесь
f(t)
= g(t)
= sin
t,
так как 
.
Искомый оригинал получаем, вычисляя интеграл по переменной , считая t=cоnst (постоянной величиной):
(t)
=
=
=
=
=
.
3.3.11 Предельные соотношения.
Пусть f(t), f(t) являются оригиналами, тогда выполняются соотношения:
pF(p)
=
f(t) = f(0),
pF(p)
=
f(t) = f().
Действительно, ранее получено (дифференцирование оригинала), что
Lf (t) = pF(p) - f(0).
Данное изображение является функцией, аналитической при p:
(pF(p)
- f(0))
= 0,
pF(p)
-
f(0)
= 0,
pF(p)
= f(0).
Также по свойству дифференцирования оригинала имеем:
При условии p0:
=
=
(f()
- f(0)) =
(pF(p)
- f(0)),
pF(p)
=
f(t).
Предельные соотношения удобно использовать в тех случаях, когда изображение F(p) имеет сложный вид и трудно указать точный оригинал, соответствующий изображению. Предельные соотношения помогают оценить начальное f(0) и конечное f() значения функции оригинала.
Пример 3.17 Найти предельные соотношения изображения
F(p)
=
Оценки начального и конечного значений f(t) имеют вид:
pF(p)
=
= 1 = f(0),
pF(p)
=
= 0 = f().
Пример
3.18 Найти
преобразование Лапласа функции
.
При
-1<<0
значение функции f(0)
=
и функция не является оригиналом (не
выполняется условие определения
оригинала). Однако при >-1
и Re
p>0
интеграл
сходится. Вычисляя интеграл при помощи
замены переменной pt
= ,
получаем
или
t
;
> -1; Re
p
> 0.
Здесь Г() - гамма функция Эйлера, которая может быть найдена по таблице.
В
частном случае
= -1/2 Г(1/2) =
и 1/t
1/ p
.
Основные изображения для функций-оригиналов приведены в табл. 1
3.4
ВОССТАНОВЛЕНИЕ ОРИГИНАЛА ПО ИЗОБРАЖЕНИЮ
(ОБРАТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА)
3.4.1 ПРОСТЕЙШИЕ ПРИЕМЫ ВОССТАНОВЛЕНИЯ
ОРИГИНАЛОВ
Во
многих случаях восстановить оригинал
по
известному изображению F(p)
можно, используя таблицу соответствия
оригиналов и изображений, а также их
свойства.
Рассмотрим примеры нахождения оригинала изображения F(p).
Пример 3.19.
Здесь использовали таблицу и свойство смещения изображения.
Пример
3.20.
Эта же задача может быть решена и с использованием изображения свертки:
Пример 3.21.
Здесь использовали таблицу и свойство запаздывания оригинала.
Пример
3.22. 
Первый способ основан на разложении изображения в сумму элементарных дробей:
Второй способ также основан на разложении в сумму дробей и использовании свойства интегрирования оригинала:
так как
3.4.2 ФОРМУЛА ОБРАЩЕНИЯ
Пусть справедливо соотношение:
f(t) F(p).
Если функция-оригинал f(t) непрерывна в точке t и имеет в этой точке непрерывные конечные производные, то
f(t)
=
Здесь
- показатель роста функции-оригинала
f(t).
Для
доказательства рассмотрим вспомогательную
функцию g(t)
= e
f(t),
>
.
Функция F(p)
= F(+i)
является преобразованием Фурье для
функции g(t),
так как
F(p)
= F(i)
=
=
Для обратного преобразования Фурье получаем:
Делая замену переменной p = +i, dp = id, получаем:
Пример
3.23. Найти
оригинал изображения F(p)
=
(
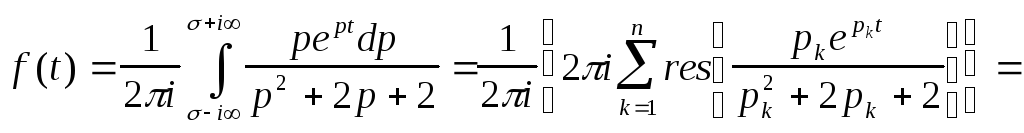
- полюсы
первого порядка),
Таким образом, по известному изображению F(p) оригинал f(t) может быть восстановлен путем вычисления интеграла обращения. Интеграл обращения может быть вычислен с применением теории вычетов. Поэтому при нахождении оригиналов обычно используют теоремы разложения, которые следуют непосредственно из формулы обращения.
3.4.3 ПЕРВАЯ ТЕОРЕМА РАЗЛОЖЕНИЯ
Пусть изображение Лапласа F(p) является функцией, аналитической в окре-стности p= (p>R) и разложение в ряд Лорана в окрестности p= имеет вид:
Тогда
оригиналом является функция f(t)(t),
где 
Для доказательства подставим разложение F(p) в ряд Лорана в формулу обращения:
Несобственный интеграл вычисляем, применяя теорию вычетов.
Особая точка p=0 является полюсом порядка k:
Непосредственно
видно, что: 
Тогда получаем:
Пример 3.24. Найти функцию-оригинал для функции-изображе-ния:
Восстановим оригинал f(t)(t). Для этого разложим функцию в ряд Лорана:
Отсюда
Сопоставляя это разложение с формулой Маклорена:
,
получаем
начальное значение функции f(0)=-1,
начальную скорость изменения функции
f
(0)=
Пример
3.25. F(p)
=
Функция
является аналитической в окрестности
p=:
F(p)=0.
Разложение в ряд Лорана для такой функции
можно выполнить путем операции деления
многочленов:
Используя таблицу, получаем:
F(p)
=
Сопоставляя полученное выражение с разложением Маклорена, получаем:
f(0)=0, f (0)= - 1.
3.4.4 ВТОРАЯ ТЕОРЕМА РАЗЛОЖЕНИЯ
Пусть изображение Лапласа F(p) является правильной дробью:
Тогда оригиналом является функция f(t)(t), где
Сумма вычетов берется по всем особым точкам, лежащим в конечной части комплексной плоскости.
Если изображение F(p) является неправильной дробью, то необходимо выделить целую часть и при нахождении оригинала использовать свойство линейности.
Доказывается вторая теорема разложения непосредственным вычислением интеграла обращения по теореме о вычетах:
где вычеты берутся по всем особым точкам, лежащим в конечной части комплексной плоскости: Re p<.
Покажем, как находятся оригиналы f(t) при помощи второй теоремы разложения. При этом будем рассматривать те же задачи, что решали ранее другими методами.
Найти оригиналы функций-изображений.
Пример
3.26. 
Так
как дробь правильная, сразу находим
особые точки: p
=
- 23i,
которые являются простыми полюсами.
Сумму вычетов в комплексно сопряженных
точках удобно находить по формуле:
res(F(p)e
)
+
res(F(p)e
)
=
2Re res(F(p)e
)
.
Пример
3.27. F(p)
=
Пример
3.28. F(p)
=
Пример
3.29. F(p)
=
Пример
3.30.
F(p) =
Табл. 1
ТАБЛИЦА ОСНОВНЫХ ПРЕОБРАЗОВАНИЙ ЛАПЛАСА
|
f(t) |
F(p) |
f(t) |
F(p) |
|
(t) |
1 |
t |
n!/(p-a)n+1 |
|
(t) |
1/p |
f (t) |
pF(p)-f(0) |
|
1 |
1/p |
f (t) |
p2F(p)-pf(0) |
|
e |
1/(p-a) |
e |
F(p-a) |
|
sint |
|
tsint |
|
|
cost |
|
tcost |
|
|
sht |
|
tsht |
|
|
cht |
|
|
|
|
e |
|
|
|
|
e |
|
|
|
|
t |
1/p2 |
|
|
|
tn |
n!/pn+1 |
|
|
|
tn , n- нецелое число |
Г(n+1)/pn+1 |
|
|
e
f(t)
sint
cost
ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЙ ЛАПЛАСА ДЛЯ РЕШЕНИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ И СИСТЕМ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
4.1 РЕШЕНИЕ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ ОПЕРАТОРНЫМ МЕТОДОМ
Задача Коши для линейного уравнения:
состоит в нахождении частного решения y(t) по заданным начальным условиям
y(0)=y0;
y(0)=y0;
...; y
(0)=y
.
Полагаем, что правая часть уравнения x(t) и искомая функция y(t) являются оригиналами. Тогда для них существует преобразование Лапласа:
Применяя правило дифференцирования оригинала
................................
и используя свойство линейности, переходим в исходном дифференциальном уравнении от оригиналов к изображениям. При этом исходное дифференциальное уравнение переходит в алгебраическое уравнение относительно Y(p):
Тогда
B этом выражении стоящий в знаменателе многочлен K(p) называется характеристическим многочленом, а функция M(p) выражает влияние начальных условий.
Решение
исходного дифференциального уравнения
получаем, возвращаясь к оригиналам Y(p)
y(t).
Пример 4.1. Найти частное решение линейного дифференциального уравнения второго порядка
Переходя
к изображениям
получаем операторное уравнение
Решая
его, получаем Y(p):
Возвращаясь к оригиналам, находим решение исходного уравнения:
Пример 4.2. Найти частное решение дифференциального уравнения
Переходя к изображениям:
получаем алгебраическое уравнение
Операторное решение Y(p) получаем в виде:
Переходя к оригиналу, например, по второй теореме разложения, найдем y(t):
Пример 4.3. Найти частное решение уравнения
Переходя
к изображениям
,
получаем операторное уравнение
и его решение
Переходя к оригиналам, получаем искомое решение:
При решении операторным способом правая часть уравнения может быть задана функцией, имеющей точки разрыва 1-го рода.
Пример 4.4. Найти частное решение уравнения, для которого правая часть x(t) приведена на (рис. 4.1)
Переходя к изображениям:
получаем алгебраическое уравнение
Тогда решение запишется в виде:
Переходя к оригиналам и используя свойство запаздывания оригинала, получаем решение:
Результат записывается следующим образом:
4.2 ЗАПИСЬ РЕШЕНИЙ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ТЕОРИИ УПРАВЛЕНИЯ. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ
Линейное дифференциальное уравнение в общем виде
м
оделирует
систему вход-выход. Здесьx(t)-
некоторое входное (внешнее) воздействие
на систему, а y(t)-
выходной сигнал (отклик системы на
входное воздействие) (рис. 4.2).
При переходе к изображениям при нуле-
вых начальных условиях получаем алге-
браическое уравнение
Передаточной функцией H(p) при нулевых начальных условиях называют отношение изображения сигнала на выходе Y(p) к изображению сигнала на входе X(p):
H(p)=
Тогда изображение сигнала на выходе системы легко получается умножением изображения сигнала на входе на передаточную функцию:
Y(p)=H(p)X(p).
Переходя затем к оригиналу, получаем отклик системы на входное воздействие
.
Пример 4.5. Найти ток для простейшей RL - цепи (рис. 4.3).
З
аписывая
уравнения Кирхгофа
простейшей RL- цепи с входным
напряжением U(t), получаем диф-
ференциальное уравнение
Рис.
4.3
Переходя к изображениям с учетом начального условия J(0)=0, запишем алгебраическое уравнение для искомого тока J(p):
LpJ(p)+RJ(p)=U(p),
решая которое, получаем:
J(p) (Lp +R)=U(p),
,
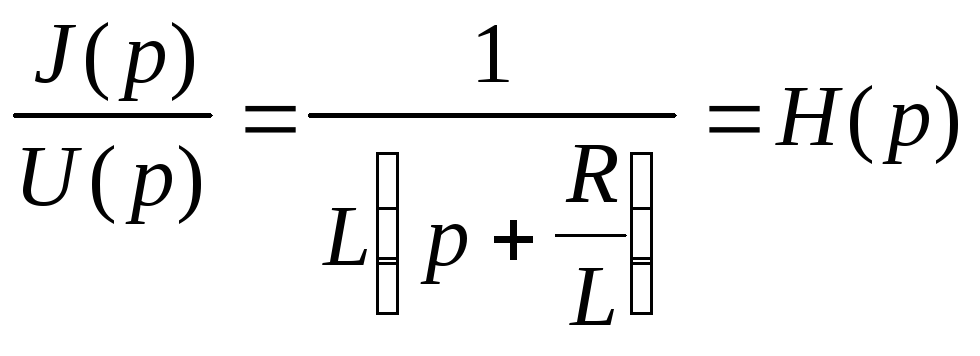Таким образом, определив передаточную функцию H(p), можно найти реакцию системы (ток) при любом внешнем воздействии (входном напряжении).
Пусть U(t) имеет вид прямоугольного импульса
Такую
функцию легко записать одной формулой,
применяя функцию Хевисайда 
:
Используя свойство линейности и свойство запаздывания оригинала, получаем изображение для U(t):
В результате ток на выходе системы
Возвращаясь к оригиналу, получаем
зависимость тока от времени (рис. 4.4):
При переходе к оригиналу воспользовались второй теоремой разложения:
С учетом свойства запаздывания оригинала решение запишется следующим образом:
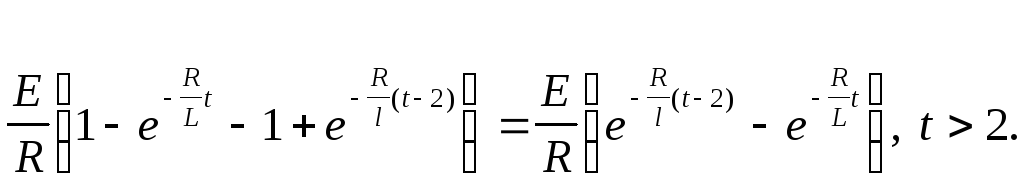
Пусть
входное напряжение
Тогда ток J(p)
будет задаваться выражением:
Возвращаясь к оригиналу, получаем:
4.3 ЗАПИСЬ РЕШЕНИЯ ЛИНЕЙНОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПРИ ПОМОЩИ СВЕРТКИ. ФУНКЦИЯ ГРИНА
Рассмотрим линейное дифференциальное уравнение в операторной форме при нулевых начальных условиях:
Y(p)=H(p)X(p).
Пусть
входное воздействие является импульсной
функцией
Поскольку 
,
изображение выходного сигнала совпадает
с передаточной функцией:
Y(p)=H(p).
Функцией Грина (или функцией веса в теории управления) линейного дифференциального уравнения называют отклик системы на импульсное входное воздействие или оригинал передаточной функции:
Поскольку
изображение выходного сигнала Y(p)
является произведением изображений,
то и оригинал y(t)
можно представить как свертку оригиналов
x(t)
и 
(t)
:
Таким образом, при известной функции Грина можно найти отклик системы на любое внешнее воздействие.
Пример 4.6. Решить пример 4.5 с использованием свертки.
Для RL - цепи оригинал передаточной функции H(p) или отклик системы на импульсное воздействие имеет вид:
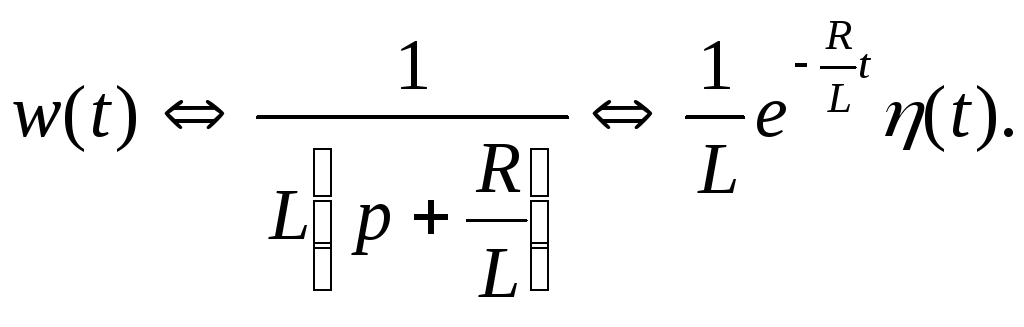
Тогда
отклик системы на прямоугольный импульс
получаем с использованием свертки:
Как видно из данного выражения, результат совпадает с полученным ранее.
Пример 4.7. Найти частное решение дифференциального уравнения
,
Взяв
в качестве правой части импульсную
функцию 
и переходя к изображениям,
получим
передаточную функцию:
H(p):
Возвращаясь к оригиналам, получаем функцию Грина:
Теперь, задавая любым образом правую часть x(t), можно найти решение дифференциального уравнения.
Пусть
Тогда
Пусть
то решение имеет вид:
Пусть
Тогда решение имеет вид:
Вычисляя
интегралы с помощью замены переменной
получаем:
Пример 4.8. Найти частное решение дифференциального уравнения
,
.
Правая часть уравнения задана функцией (рис. 4.5):
Д
С
учетом того, что функция Грина для этого
уравнения имеет вид 
получаем решение y(t):
Существует и другой способ записи решений дифференциальных линейных уравнений с использованием свертки. Он основан на формуле Дюамеля. Характеристикой системы в этом случае служит переходная функция h(t), которая определяется как реакция (отклик) системы на постоянное воздействие
Из
последнего выражения и свойства
интегрирования оригинала следует, что
функция 
(t)
и h(t)
связаны соотношениями:
С учетом того, что
,
оригинал y(t) можно записать по формуле Дюамеля следующим образом:
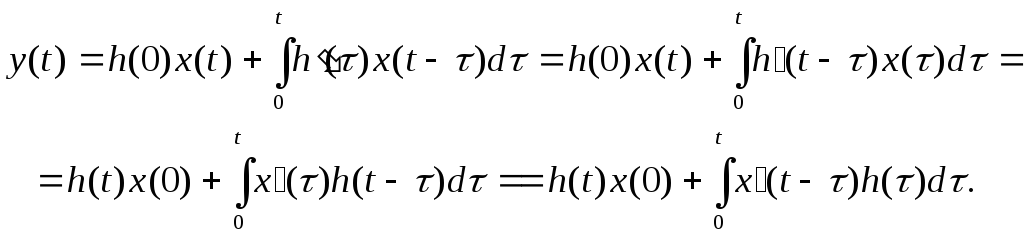
Заметим, что при условии h(0)=0 две первых формы записи решения совпадают с записью
Также напомним, что в силу условий вывода формулы Дюамеля приведенные формулы можно непосредственно использовать для непрерывных функций x(t). В том случае, если функция x(t) имеют точки разрыва первого рода, следует точно записывать функцию x(t), учитывая скачкообразное изменение функции в точках разрыва или другим способом учесть эти изменения. Например, если правая часть x(t) имеет вид:
то и формула Дюамеля принимает вид:
Переходя к оригиналам, получаем
Применим формулу Дюамеля для решения примера 4.8.
П
роизводная
функции, стоящей в правой части уравнения
равна:
Рис. 4.6
Переходная функция системы имеет вид:
Тогда вычисляя по формуле
с учетом того, что x(0) = 1; x(2) = 2, получаем:
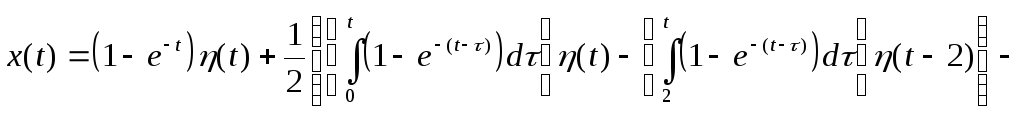
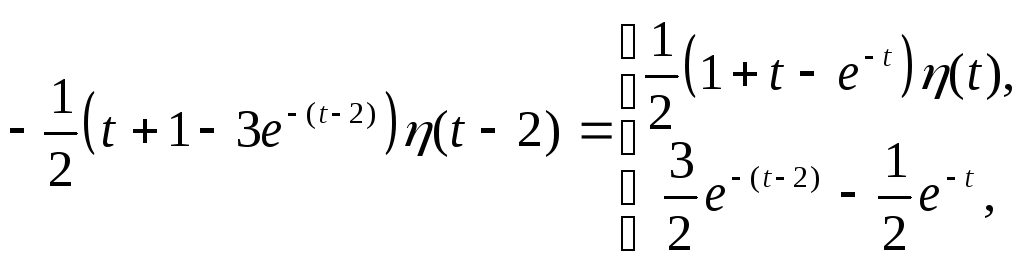
Пример 4.10. Найти частное решение дифференциального уравнения
Переходную функцию для данного дифференциального уравнения можно получить, интегрируя функцию Грина
Проверить
самостоятельно, что при 
и 
вычисления по формуле:
дадут
тот же результат, что и получен ранее
другими способами, соответственно: