
4.4 Решение систем линейных дифференциальных уравнений операторным методом. Матричная функция отклика
Рассмотрим систему линейных дифференциальных уравнений

c
начальными условиями
![]()
Считая
функции ![]() функциями-оригиналами и переходя к
изображениям, получаем систему
алгебраических уравнений относительно
переменных X(p),
Y(p):
функциями-оригиналами и переходя к
изображениям, получаем систему
алгебраических уравнений относительно
переменных X(p),
Y(p):

Решая эту систему методом исключений, методом Крамера или матричным методом, находим изображения X(p), Y(p). Возвращаясь к оригиналам, получаем решение:
![]()
Рассмотрим более подробно матричный метод решения полученной алгебраической системы, вводя следующие матрицы:
 матрица
коэффициентов системы;
матрица
коэффициентов системы;
![]()
![]() матрица
искомых функций;
матрица
искомых функций;
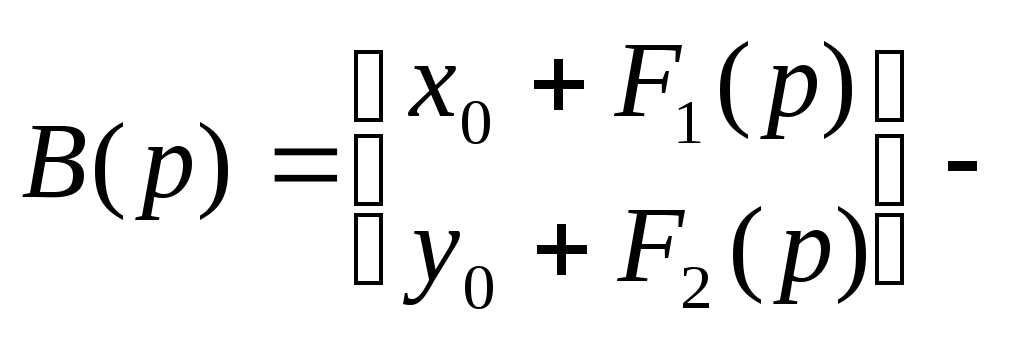 матрица,
включающая начальные условия и изображения
правых частей.
матрица,
включающая начальные условия и изображения
правых частей.
Исходная система записывается как матричное уравнение:
![]()
решением которого является матрица:
![]()
Здесь
![]() называется преобразователем Лапласа
фундаментального решения системы или
матрицей
Грина. По
правилу нахождения обратной матрицы
получаем:
называется преобразователем Лапласа
фундаментального решения системы или
матрицей
Грина. По
правилу нахождения обратной матрицы
получаем:

Оригинал
![]() матрицы
матрицы ![]() называют
матричной
функцией отклика,
фундаментальным решением или матричной
функцией Грина:
называют
матричной
функцией отклика,
фундаментальным решением или матричной
функцией Грина:

Таким образом, решение системы записывается в виде матрицы:

Переходя к оригиналам в каждой из строк этой матрицы, получаем окончательное решение системы:

Можно записать решение, используя свертку оригиналов:

Отметим,
что матричная функция отклика ![]() совпадает
с матрицей
совпадает
с матрицей ![]() , которая представляет собой фундаментальное
решение системы, а приведенная выше
форма записи решения совпадает с формой
записи решения с использованием матричной
экспоненты:
, которая представляет собой фундаментальное
решение системы, а приведенная выше
форма записи решения совпадает с формой
записи решения с использованием матричной
экспоненты:

Пример 4.11. Найти решение системы дифференциальных уравнений:

![]()
Переходя к изображениям:
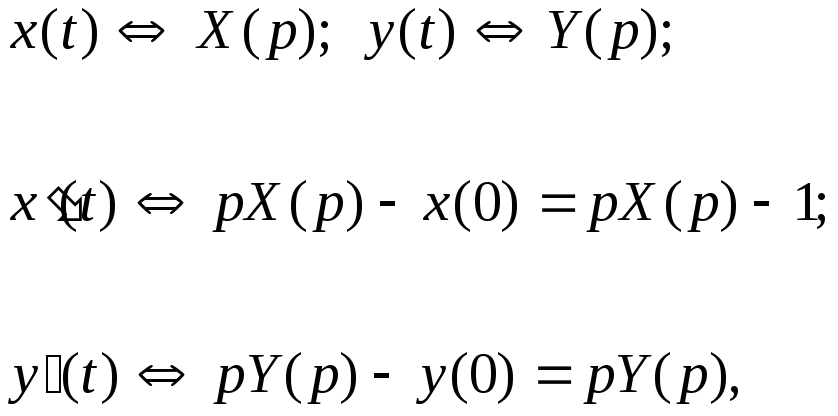
получаем систему алгебраических уравнений:

Матрица A(p) этой системы имеет вид:
![]()
обратная
матрица ![]()
![]()
Переходя к оригиналам:

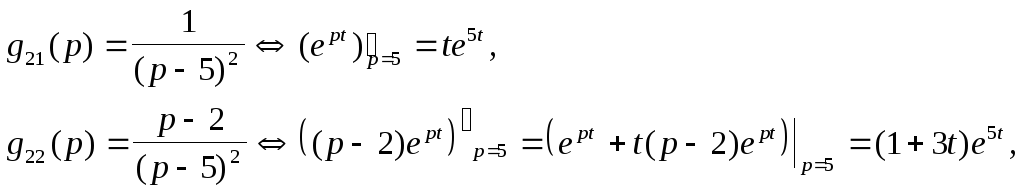
записываем
матрицу отклика :
![]()
Решение системы запишем двумя способами.
Первый
способ.
Введем
матрицу 

Решение системы имеет вид :

Второй способ. Используем матрицу отклика и свертку оригиналов:
![]()
![]()
![]()
![]()
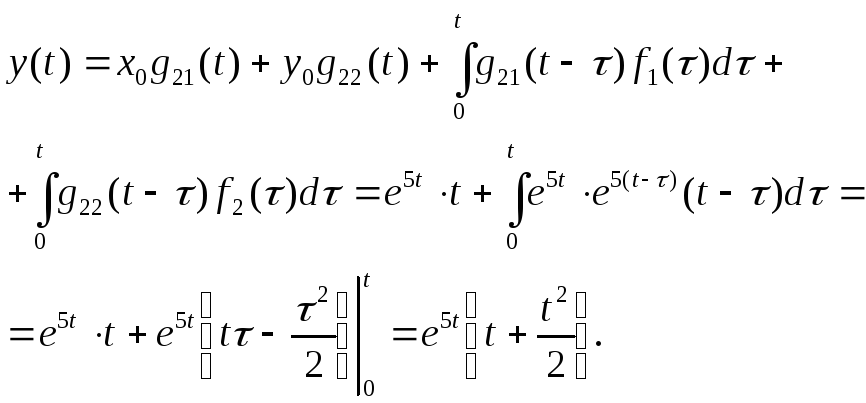
![]()
Пример
4.12. Найти
токи в электрическом контуре при
последовательном замыкании ключей ![]() (рис. 4.7).
(рис. 4.7).
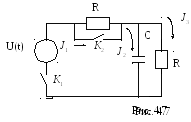
R
= 10 Ом,
С = 10![]() Ф,
Ф,
U![]() (0)
= 0.
(0)
= 0.
Пусть
ключ ![]() разомкнут, замкнут только ключ
разомкнут, замкнут только ключ ![]() Тогда при выбранных начальных условиях
напряжение на конденсаторе имеет вид:
Тогда при выбранных начальных условиях
напряжение на конденсаторе имеет вид:
![]()
Записывая уравнения Кирхгофа, получаем систему уравнений:

исключая
![]() получим:
получим:

Далее переходим к изображениям с учетом начальных условий
![]() :
:
![]()

Матрица коэффициентов системы имеет вид:

ее определитель равен:
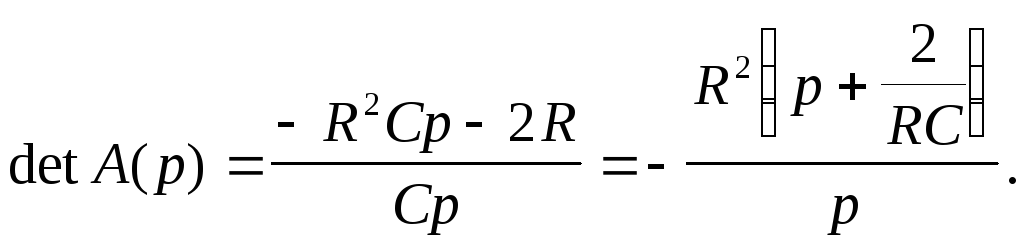
Обратная матрица или матрица Грина записывается следующим образом:

Таким
образом, при любом входном напряжении
![]() ток в системе равен:
ток в системе равен:
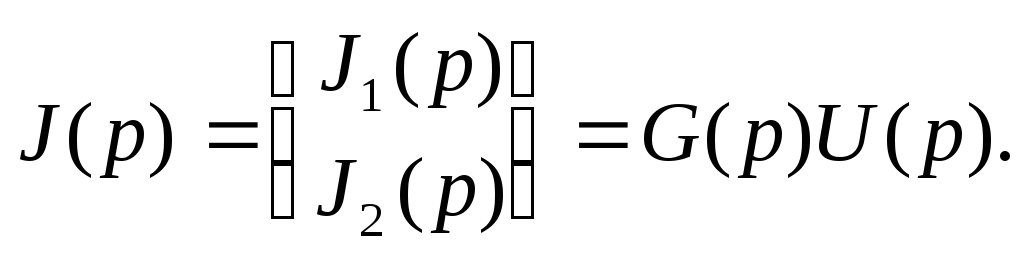
Пусть
U(t)=E=20
B.
Тогда
![]()

Возвращаясь к оригиналам, окончательно получаем:

![]()

Далее
находим переходные токи после
замыкания ключа ![]() ,
при U(t)=E=20
B.
Начальные условия в этой задаче уже не
являются нулевыми. С учетом того, что
,
при U(t)=E=20
B.
Начальные условия в этой задаче уже не
являются нулевыми. С учетом того, что ![]() напряжение на конденсаторе будет
напряжение на конденсаторе будет ![]() Уравнения Кирхгофа переписываются
следующим образом:
Уравнения Кирхгофа переписываются
следующим образом:

Переходя к изображениям, получаем систему алгебраических уравнений:

Матрица коэффициентов системы имеет вид:

Обратная матрица (матрица Грина) запишется:

Ток в системе находится как произведение матриц:

Возвращаясь к оригиналам, находим переходные токи:

Заметим, что исходную систему можно решить и методом исключений, сведя к одному дифференциальному уравнению. Так, система

равносильна дифференциальному уравнению:
![]()
Переходя к изображениям Лапласа при нулевых начальных условиях, определяем передаточную функцию системы H(p) (проводимость):

![]()
функцию веса или функцию Грина:
![]()
переходную функцию:

Используя эти функции, можно найти реакцию системы на любое входное напряжение U(t).
Пример
4.13. Найти
токи в электрической цепи при замыкании
ключей ![]() (рис. 4.8).
(рис. 4.8).

Рис.
4.8
Запишем
уравнения Кирхгофа и получим систему
дифференциальных уравнений при замыкании
ключа ![]()

Исключая
переменную ![]() получаем систему из двух уравнений:
получаем систему из двух уравнений:

Перейдем к изображениям с учетом нулевых начальных условий
![]()

Матрица коэффициентов системы имеет вид:
![]()
обратная матрица (матрица Грина) записывается:

Cледовательно,
ток в системе после замыкания ключа ![]() находится как произведение матриц:
находится как произведение матриц:

Здесь
приняли ![]()


Установившееся
значение тока ![]() при
при ![]() Поэтому при замыкании ключа
Поэтому при замыкании ключа ![]() начальные условия уже не будут нулевыми:
начальные условия уже не будут нулевыми:
![]() Для падения напряжения на катушке
индуктивности справедливо:
Для падения напряжения на катушке
индуктивности справедливо:
![]()
Система уравнений Кирхгофа принимает в операторной форме вид:
Решение системы находим методом исключений:
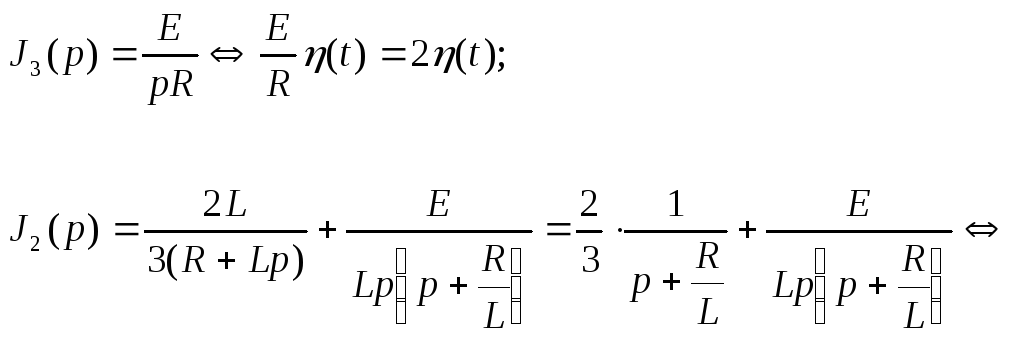

Исходную
систему (при разомкнутом ключе ![]() )
можно преобразовать в равносильное
дифференциальное уравнение:
)
можно преобразовать в равносильное
дифференциальное уравнение:
![]()
Переходя к изображениям при нулевых начальных условиях, получаем передаточную функцию H(p):

а также другие характеристики системы: функцию Грина (функцию веса)
![]()
и переходную функцию системы

Z - ПРЕОБРАЗОВАНИЯ И ДИСКРЕТНЫЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
ПОНЯТИЕ ФУНКЦИИ ДИСКРЕТНОГО АРГУМЕНТА И РЕШЕТЧАТОЙ ФУНКЦИИ
В
этом разделе будем рассматривать
функции, которые не являются функциями
непрерывного аргумента, а представляют
собой счетные последовательности: ![]()
Символ [....] ввели для обозначения дискретной переменной n (дискретного времени), принимающей только целочисленные значения.
Кроме
того, при решении некоторых задач
специально переходит от непрерывных
функций к дискретным, взяв периодическую
выборку из непрерывной функции: ![]()
Здесь
T - некоторый выбранный период. Например,
от непрерывной экспоненты ![]() можно перейти к ее дискретному аналогу,
вычислив значение функции в точках,
кратных, выбранному периоду T:
можно перейти к ее дискретному аналогу,
вычислив значение функции в точках,
кратных, выбранному периоду T:
![]()
По
аналогии с функцией-оригиналом для
непрерывных функций вволят решетчатую
функцию или дискретную функцию -оригинал:
![]() ,
которая удовлетворяет следующим
условиям:
,
которая удовлетворяет следующим
условиям:
![]() для
всех n<0
для
всех n<0
![]()
КОНЕЧНЫЕ РАЗНОСТИ И ЛИНЕЙНЫЕ РАЗНОСТНЫЕ
УРАВНЕНИЯ
Линейные разностные уравнения играют по отношению к решетчатым функциям такую же роль как и линейные дифференциальные уравнения по отношению к непрерывным функциям. Численное интегрирование дифференциальных уравнений обычно включает в себя разностные уравнения как промежуточный этап. Действительно, при численном дифференцировании первую производную приближенно заменяют согласно соотношению:
![]()
![]()
Принимая
![]() получаем аналог первой производной -
первую прямую конечную разность:
получаем аналог первой производной -
первую прямую конечную разность:
![]()
Аналогом второй производной является вторая конечная разность:
![]()
Аналогом
производной порядка ![]() служит
служит ![]() я
конечная разность:
я
конечная разность:
![]() (5.1)
(5.1)
Для функций дискретного аргумента уравнение в конечных разностях является аналогом дифференциального уравнения для непрерывных функций:
![]() (5.2)
(5.2)
Здесь
![]() -
искомая функция,
-
искомая функция,
![]() -
заданная функция. Заменяя конечные
разности согласно (5.1), переписываем
уравнение (5.2) в виде:
-
заданная функция. Заменяя конечные
разности согласно (5.1), переписываем
уравнение (5.2) в виде:![]()
![]() (5.3)
(5.3)
Последнее
уравнение позволяет восстановить
искомую функцию ![]() по заданным начальным условиям:
по заданным начальным условиям:
![]()
Для решения разностных уравнений удобен метод Z- преобразований, которые являются аналогом преобразований Лапласа для решетчатых функций.
Z- ПРЕОБРАЗОВАНИЕ
преобразованием для числовой (действительной или комплексной) бесконечной последовательности
 называют функцию комплексного переменного
называют функцию комплексного переменного
 которая определяется как разложения
в ряд Лорана в окрестности бесконечно
удаленной точки
которая определяется как разложения
в ряд Лорана в окрестности бесконечно
удаленной точки  :
:
![]() (5.4)
(5.4)
Если
функция ![]() является решетчатой функцией и
удовлетворяет условию
является решетчатой функцией и
удовлетворяет условию ![]() то ряд Лорана (5.4) сходится в области
то ряд Лорана (5.4) сходится в области ![]() то есть вне круга с центром в начале
координат и радиусом
то есть вне круга с центром в начале
координат и радиусом ![]() Функция
Функция
![]() является в этой области аналитической
функцией.
является в этой области аналитической
функцией.
Рассмотрим
примеры нахождения Z-
преобразований для простейших решетчатых
функций ![]()
Пример
5.1. Найти
Z-преобразование
функции ![]() .
.
Разложение функции в ряд Лорана имеет вид:
![]()
Так
как данный ряд является геометрической
прогрессией со знаменателем ![]() и первым членом прогрессии, равным А,
то сумма ряда равна:
и первым членом прогрессии, равным А,
то сумма ряда равна:

Область
сходимости ряда:
![]()
В дальнейшем будем обозначать соответствие между решетчатой функцией и ее Z- преобразованием следующим образом:
![]()
Пример
5.2. Найти
Z-преобразование
для функции ![]()
Разложение функции в ряд Лорана имеет вид:

Область
сходимости ряда определяется соотношением:
![]() или
или ![]()
Пример
5.3. Найти
Z-преобразование
функции 
Разложение в ряд Лорана функции имеет вид:
![]()
Для
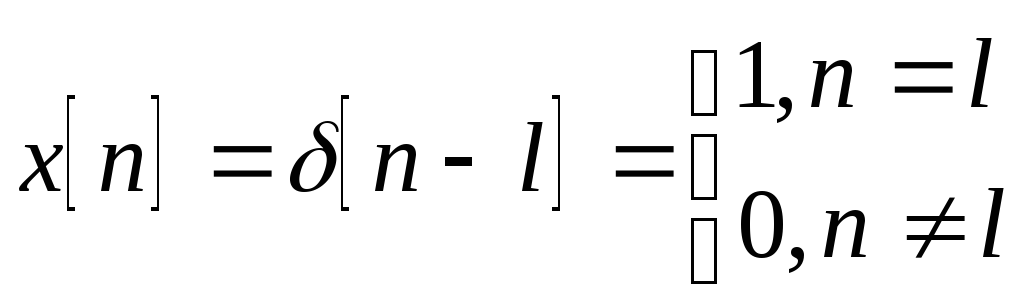 получим:
получим:
![]() так как в этом случае остается только
одно слагаемое, соответствующее
так как в этом случае остается только
одно слагаемое, соответствующее
![]()
Пример
5.4. Найти
Z-преобразование
функции ![]()
Разложение в ряд Лорана функции имеет вид:

![]()
Пример
5.5. Найти
Z-преобразование
функции ![]()
Разложение в ряд Лорана функции имеет вид:
![]()


![]()
![]()
![]()
Пример
5.6. Найти
Z-преобразование
функции ![]()
Разложение в ряд Лорана функции имеет вид:

Здесь использовали полученное ранее соотношение:
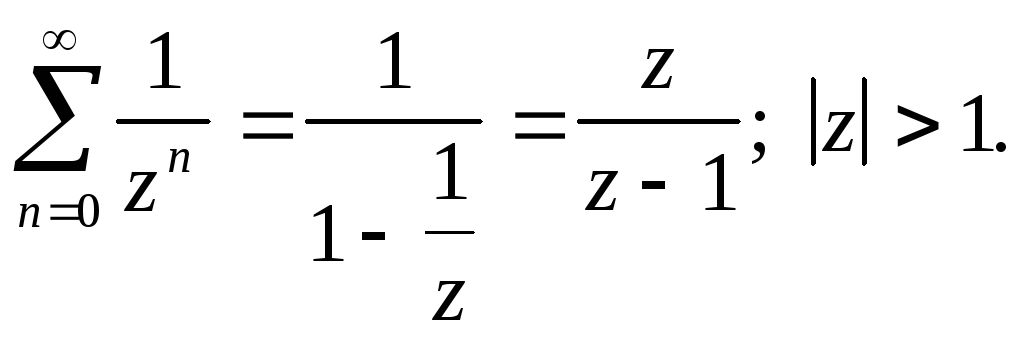
Изображения основных решетчатых функций приведены в табл. 2.
Приведем основные свойства Z- преобразований, следующие непосредственно из определения:
Линейность.
Пусть
![]() Тогда справедливо соотношение:
Тогда справедливо соотношение:
![]()
Подобие:

Дифференцирование изображения:

Запаздывание оригинала (задержка):
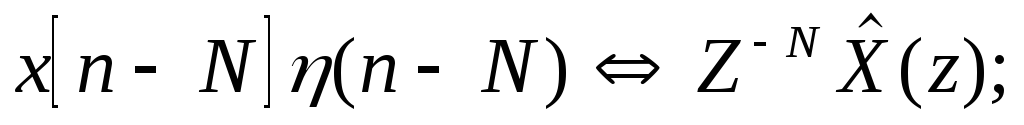
здесь
 является функцией единичного cкачка.
является функцией единичного cкачка.
Табл. 2.
Z - ИЗОБРАЖЕНИЕ ОСНОВНЫХ РЕШЕТЧАТЫХ ФУНКЦИЙ
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Опережающий сдвиг оригинала (упреждение):

Действительно, с учетом того, что

получаем доказательство первого соотношения:
![]()
Свертка:

5.4. ВОССТАНОВЛЕНИЕ ПОСЛЕДОВАТЕЛЬНОСТИ X[n] ПО Z - ПРЕОБРАЗОВАНИЮ
Поскольку
по определению функция ![]() является
суммой ряда Лорана в окрестности точки
является
суммой ряда Лорана в окрестности точки
![]() ,
то для восстановления решетчатой функции
(последовательности)
,
то для восстановления решетчатой функции
(последовательности) ![]() нужно любым способом разложить
нужно любым способом разложить ![]() в ряд Лорана и определить коэффициенты
этого разложения. Например, можно
использовать общую формулу для
коэффициентов ряда Лорана в окрестностях
в ряд Лорана и определить коэффициенты
этого разложения. Например, можно
использовать общую формулу для
коэффициентов ряда Лорана в окрестностях
![]() :
:

Сумма вычетов берется по всем особым точкам, лежащим в конечной части плоскости.
Пример 5.7. Восстановить решетчатую функцию
![]()
Восстановим x[n] двумя способами.
Способ
1. ![]() представляем суммой элементарных дробей
и записываем разложение в ряд Лорана:
представляем суммой элементарных дробей
и записываем разложение в ряд Лорана:
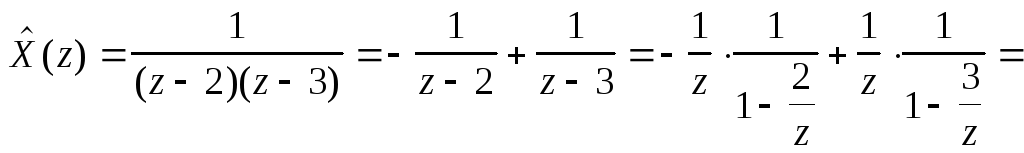
![]()
Сопоставляя
с определением ![]() :
:
![]() ,
получаем искомую последовательность:
,
получаем искомую последовательность:
![]()
Способ 2. Функцию x[n] восстанавливаем по формуле для коэффициентов ряда Лорана:
![]()
С
учетом того, что данная функция ![]() имеет простые полюсы в точках z=2
и z=3,
получаем:
имеет простые полюсы в точках z=2
и z=3,
получаем:

![]()
Примечание.
Если x[n]
- решетчатая функция, то заменяя ![]() получаем дискретное преобразование
Лапласа для x[n]:
получаем дискретное преобразование
Лапласа для x[n]:
![]()
Функция
F(q)
аналитична в области ![]() Формула обращения для дискретных
преобразований Лапласа имеет вид:
Формула обращения для дискретных
преобразований Лапласа имеет вид:
![]()
Все
изображения функций и основные свойства
изображений совпадают с аналогичными
характеристиками Z-
преобразований и могут быть получены
из них заменой ![]() .
Но поскольку все формулы при этом будут
более громоздкими, в дальнейшем для
решения задач будем использовать только
Z-
преобразования.
.
Но поскольку все формулы при этом будут
более громоздкими, в дальнейшем для
решения задач будем использовать только
Z-
преобразования.
5.5 ПРИМЕНЕНИЕ Z - ПРЕОБРАЗОВАНИЙ ДЛЯ РЕШЕНИЯ ЛИНЕЙНЫХ РАЗНОСТНЫХ УРАВНЕНИЙ И СИСТЕМ УРАВНЕНИЙ
При решении линейных разностных уравнений (5.3):

функции
x[n],
f[n]
считаем решетчатыми функциями (дискретными
оригиналами) и переходя к Z
- преобразованиям, получаем алгебраическое
уравнение относительно функции ![]() .Решив
алгебраическое уравнение, по изображению
.Решив
алгебраическое уравнение, по изображению
![]() восстанавливаем оригинал x[n]
и тем самым получаем искомую
последовательность x[n].
восстанавливаем оригинал x[n]
и тем самым получаем искомую
последовательность x[n].
Пример 5.8. Найти решение разностного уравнения:
![]()
Для решения уравнения перейдем к Z - преобразованиям:

Исходное уравнение преобразуется при этом в алгебраическое уравнение:

Для восстановления оригинала x[n] используем общую формулу коэффициентов ряда Лорана:
![]()
Поскольку
найденная функция ![]() имеет простые полюсы в точках
имеет простые полюсы в точках ![]() получаем :
получаем :


Пример 5.9. Найти решение разностного уравнения:

Перейдем к Z - преобразованиям:
![]()
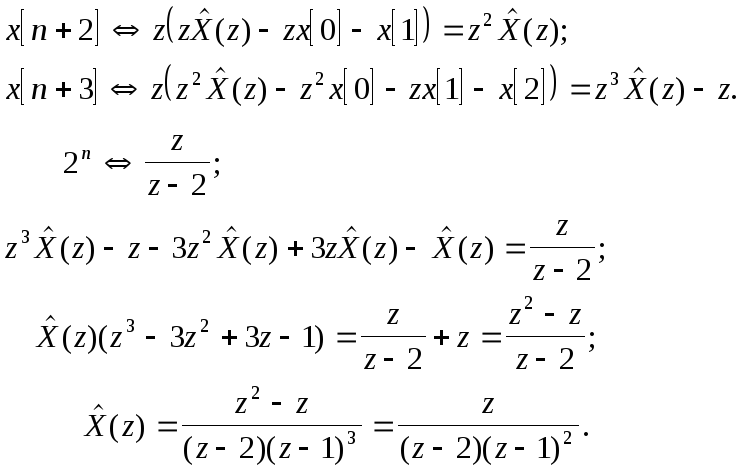
И, наконец, восстанавливаем оригинал x[n] :
![]()
![]()
Пример 5.10. Найти решение системы разностных уравнений:

![]()
Переходя к Z - преобразованиям, получаем систему алгебраических уравнений:
![]()
![]()
![]()
![]()


Решим полученную систему матричным методом, введя матрицу системы:
![]()
![]()
а
также матрицы ![]()

Записывая
исходную систему в матричном виде ![]()
находим решение:



Окончательное
решение получаем, восстанавливая
оригиналы ![]()
![]()
![]()
![]()
![]()
![]()

![]() находим
путем аналогичных преобразований:
находим
путем аналогичных преобразований:
![]()


