1.5. Угол между двумя прямыми

Рассмотрим две прямые I и II, задаваемые уравнениями ии образующиеc осью углыисоответственно.

y

I



II

x

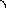
O

Тогда ,. Уголявляется внешним углом треугольника, образованного осьюи прямымиI и II. Пусть  один из углов между прямыми. Тогда или. Следовательно,

. (1.9)

Второй угол между прямыми равени. За угол между прямыми принимается наименьший неотрицательный угол из углови.

Если две прямые параллельны, то , поэтому. Условие

(1.10)

является условием параллельности двух прямых. Если же прямые перпендикулярны, то угол ,, следовательно,или

. (1.11)

Это равенство является условием перпендикулярности двух прямых с угловыми коэффициентами и.

П р и м е р 9. Найти угол между стороной треугольникаи медианой, проведенной из вершины, если,и.

Решение. Пусть точка является серединой стороны, тогда по формуле (1.3),. Составим уравнение стороны, воспользовавшись формулой (1.8);, или. Угловой коэффициентпрямой, содержащей сторону, равен. Медианазадается уравнением. Это уравнение приводится к виду. Поэтому угловой коэффициентпрямой, содержащей медиану, равен. По формуле (1.9) тангенсы углов между сторонойи медианой:,. Учитывая, что за угол между прямыми принимается наименьший положительный из углови, получаем, что угол между сторонойи медианойравен.

Замечание. Угловой коэффициент прямой, проходящей через две заданные точкиис различными абсциссами, согласно (1.7) должен удовлетворять соотношению. Если, то.

П р и м е р 10. Составить уравнение высоты, проведенной из вершины на сторону, если,и.

Решение. Прямая, содержащая сторону , проходит через точку, поэтому ее уравнение имеет вид (1. 7):. Угловой коэффициентэтой прямой. Угловой коэффициентвысоты, проведенной из вершины, находим из условия (1.11), т. е.. Воспользовавшись формулой (1. 7), получим искомое уравнение:.

1.6. Общее уравнение прямой. Неполное уравнение первой степени. Уравнение прямой в отрезках

Теорема 4. В прямоугольной системе координат любая прямая задается уравнением первой степени

, (1.12)

и уравнение (1.8) при любых коэффициентах ,и(при условии, что коэффициентыиодновременно не обращаются в ноль, т. е.) определяет некоторую прямую в прямоугольной системе координат.

Доказательство. Если прямая не перпендикулярна оси , то она задается уравнениемили. Введем обозначения, ,и получим уравнение. Если прямая перпендикулярна оси, то все ее точки имеют одинаковые абсциссы, т. е.. В этом уравнении,,.

Пусть дано уравнение . Если, то, положив,, получим уравнение прямой, не перпендикулярной оси. Если, тои, т. е.и уравнение прямой, перпендикулярной оси . Теорема доказана.

Уравнение (1.12) называется общим уравнением прямой.

Выведем уравнение прямой в отрезках. Пусть ,и. Тогда из уравнения (1.8):, или. Обозначим,, получим

. (1.13)

Уравнение (1.13) называется уравнением прямой в отрезках. Числа иравны величинам отрезков, которые прямая отсекает на осяхисоответственно.

Уравнение (1.12) является неполным уравнением прямой, если какой-либо из коэффициентов ,илиравен нулю. Возможны следующие случаи:

1. ; уравнение определяет прямую, проходящую через начало координат;

2. ;  прямая, параллельная оси и отсекающая на осиотрезок величины;

3. ;  прямая, параллельная оси и отсекающая на осиотрезок величины.

П р и м е р 11. Найти площадь ромба, диагонали которого лежат на координатных осях, а одна из сторон задается уравнением .

Решение. Ромб делится своими диагоналями на четыре равновеликих прямоугольных треугольника. Пусть прямая пересекает оси абсцисс и ординат в точкахисоответственно. Площадь ромба равна. Уравнение стороныв отрезках имеет вид:или. Таким образом, прямаяотсекает на координатных осях отрезки длиной 7 и 3 ед. Следовательно,, а площадь ромба равна 42 (кв. ед.).