1.2. Вычисление площади треугольника через координаты вершин

Теорема 3. Пусть точки ,иявляются вершинами треугольника. Тогда площадь этого треугольника может быть вычислена по формуле:

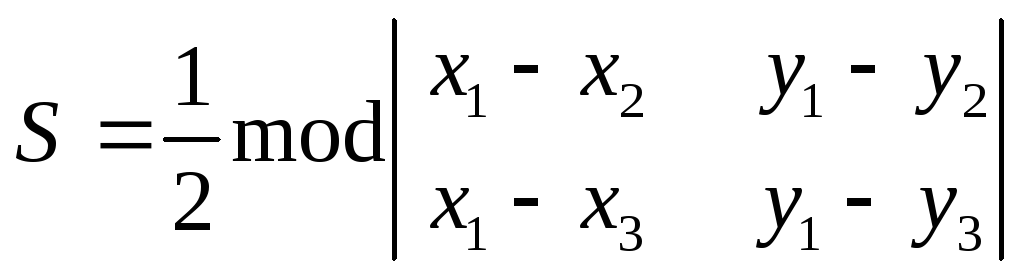. (1.4)

Доказательство. Рассмотрим треугольник АВС, расположенный в плоскости Оху. Площадь этого треугольника равна разности площадей трапеции К₁АВК₂ и треугольников К₁АС и СВК₂.. Найдем площадь трапеции К₁АВК₂ и треугольников К₁АС и СВК₂:

,

,

.

у

В (х₂; у₂)

А (х₁; у₁)

О

х

К₂ (х₂; у₃)

К₁ (х₁; у₃)

С (х₃; у₃)

Таким образом, .

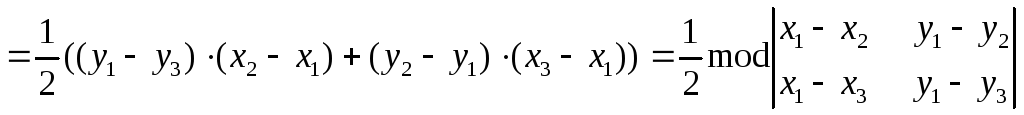Для любого другого расположения точек формула доказывается аналогично. Теорема доказана.

П р и м е р 5. Вычислить площадь параллелограмма , если известны координаты его смежных вершин,и точкипересечения его диагоналей.

Решение. Параллелограмм делится диагоналями на четыре равновеликих треугольника, поэтому . Площадь треугольниканайдем по формуле (1.4):. Таким образом,(кв. ед.).

П р и м е р 6. Одна из вершин треугольника находится в начале координат, а вторая вершинаимеет координаты. Найти координаты третьей вершины, находящейся на оси ординат, если площадь треугольникаравна 7 кв. ед.

Решение. Вершина находится на оси ординат, поэтому ее абсцисса равна нулю, т. е. точкаимеет координаты. Воспользуемся формулой (1.4) для нахождения площади треугольника, получим:. Так как площадь треугольникаравна 7 кв. ед., относительнополучаем уравнение, т. е.. Таким образом, вершинаимеет координатыили.

1.3. Уравнение прямой с угловым коэффициентом

Пусть дана некоторая прямая.

Определение. Углом  наклона данной прямой к оси называется угол, на который надо повернуть ось, чтобы ее положительное направление совпало с одним из направлений прямой. Обычно в качестве угла берут наименьший положительный из данных углов.

Определение. Угловым коэффициентом прямой называется тангенс ее угла наклона, т. е.

. (1.5)

у

y

M(x, y)

B



N



b

х

C

О

Если , то прямая параллельна оси . В случаепрямая параллельна оси.

Выведем уравнение прямой, если известны ее угловой коэффициент и величина, отсекаемая прямой на оси(т. е. прямая не перпендикулярна оси).

Из треугольника :. Далее,,. Таким образом,, или

. (1.6)

Уравнение (1.6) называется уравнением прямой с угловым коэффициентом , отсекающей на осивеличину. Если, то уравнение (1.6) принимает види прямая, задаваемая этим уравнением, параллельна оси.

Любая прямая, не параллельная оси , задается уравнением вида (1.6), и любое уравнение вида (1.6) определяет прямую, не параллельную оси.

1.4. Уравнение прямой, проходящей через данную точку

Выведем уравнение прямой, проходящей через точку , с угловым коэффициентом.

Прямая с заданным угловым коэффициентом имеет уравнение , в котором величинанеизвестна. Прямая проходит через точку, поэтому координаты этой точки удовлетворяют уравнению прямой, т. е.или. Следовательно, искомое уравнение имеет видили

. (1.7)

Замечание. Если прямая проходит через точку параллельно оси, то ее уравнение имеет вид.

Выведем уравнение прямой, проходящей через две заданные точки и. Запишем уравнение прямой в виде (1.7):, где неизвестный коэффициент. Искомая прямая проходит через точку , поэтому выполняется равенство.

Если , то искомая прямая параллельна осии имеет вид. Если, тои уравнение (1.7) принимает вид. В случаепрямая параллельна осии задается уравнением. Если же, уравнение прямой, проходящей через две заданные точки, имеет вид

. (1.8)

П р и м е р 7. Составить уравнение прямой, проходящей через точку и составляющей с осью абсцисс угол.

Решение. По формуле (1.5) угловой коэффициент прямой . Согласно формуле (1.7) искомое уравнение прямой имеет видили.

П р и м е р 8. Составить уравнения сторон треугольника, вершины которого находятся в точках ,и.

Решение. Для того чтобы составить уравнения сторон указанного треугольника, воспользуемся формулой (1.8) уравнения прямой, проходящей через две точки с различными абсциссами и ординатами. Сторона задается уравнением, или. Для стороныуравнение имеет вид, или. Уравнение третьей стороны:, т. е..