2.7. Выражение векторного произведения через координаты векторов

Из определения и свойств скалярного произведения векторов следует, что для базисных векторов ,,выполняются соотношения

, ,,,,. (2.26)

Теорема 12. Если векторы изаданы своими координатами, т. е.,, то векторное произведение векторовивычисляется по формуле

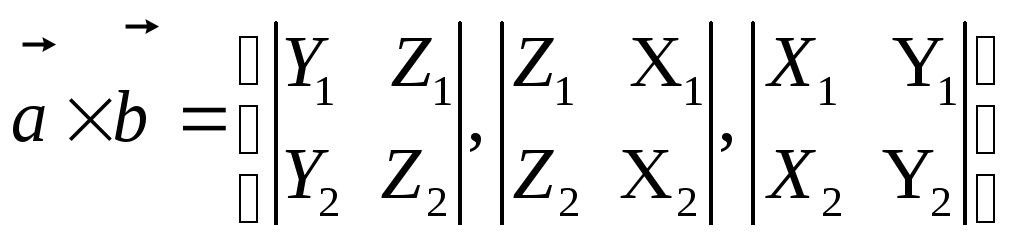, (2.27)

или .

Доказательство. Разложим векторы ипо базису,,, получим,. Тогда по свойствам векторного произведения векторов, используя формулы (2.26), имеем:=. Теорема доказана.

Следствие. Если векторы иколлинеарны, то их координаты пропорциональны, т. е.

. (2.28)

Доказательство. Если векторы иколлинеарны, то. Из формулы (2.27) получаем, что,,. Из этих равенств следует (2.28). Следствие доказано.

Соотношения (2.28) называются условием параллельности (коллинеарности) двух векторов.

Следствие. Если векторы изаданы своими координатами, т. е.,, то векторное произведение векторовивычисляется по формуле

. (2.29)

Доказательство. Разложим определитель по первой строке, получим=++=.

П р и м е р 26. Известно, что ,и. Найти длину векторного произведения векторови.

Решение. По определению векторного произведения , где угол между векторами. По формуле (2.22) имеем: . Учитывая, что угол между векторами не превышает, из основного тригонометрического тождества получим:. Таким образом,.

П р и м е р 27. Даны точки ,и. Вычислить площадьтреугольника.

Решение. Площадь треугольникаравна половине площадипараллелограмма, построенного на векторахи, т. е.. Согласно (2.4),, поэтому по формуле (2.29) имеем:. Тогда.

П р и м е р 28. Найти вектор , зная, что он перпендикулярен векторамии удовлетворяет условию.

Решение. Пусть вектор имеет координаты. Тогда условиеможно записать в виде. Векторперпендикулярен векторами, поэтому он коллинеарен вектору. По формуле (2.29). Условие коллинеарности векторовисогласно (2.28) имеет вид. Поэтому для неизвестныхполучили систему уравнений, решив которую найдем, что.

2.8. Смешанное произведение трех векторов

Пусть даны три произвольных вектора ,и.

Определение. Смешанным произведениемтрех векторов ,,называется скалярное произведение векторана векторное произведение векторови, т. е.

. (2.30)

Геометрический смысл смешанного произведения раскрывает следующая теорема.

Теорема 13. Смешанное произведение равно объему параллелепипеда, построенного на приведенных к общему началу векторах,и, взятому со знаком плюс, если тройка векторовправая, и со знаком минус, если тройкалевая. Если же векторы,икомпланарны, то.

Доказательство. Если векторы иколлинеарны, то векторы,икомпланарны. Для компланарных векторовипо свойству векторного произведения, поэтому по свойству скалярного произведения, т. е. для компланарных векторов теорема доказана.

Пусть векторы ,ине компланарны. Приведем эти векторы к общему началу. По формуле (2.23), где площадь параллелограмма, построенного на приведенных к общему началу векторах и, орт векторного произведения . Тогда

. (2.31)

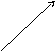
Проекция вектора на ось, определяемую вектором, с точностью до знака равна высотепараллелограмма, построенного на приведенных к общему началу векторах,и, при условии, что основанием служит параллелограмм, построенный на векторахи.

О

Таким образом, правая часть равенства (2.31) с точностью до знака равна объему параллелепипеда, построенного на векторах ,и. Если векторыилежат по одну сторону от плоскости, определяемой векторамии, то, если же векторыилежат по разные стороны от этой плоскости, то. Векторы,иобразуют правую тройку по определению векторного произведения, таким образом,, если векторы,и(соответственно векторы,и) образуют правую тройку, и, если тройка векторовлевая.

Если векторы ,икомпланарны, то векторлежит в плоскости векторови, следовательно,, и. Теорема доказана.

Из этой теоремы следует, что объем параллелепипеда, построенного на приведенных к общему началу векторах ,и, вычисляется по формуле

. (2.32)

Следствие 1. Для любых трех векторов ,исправедливо равенство

. (2.33)

Доказательство. Из переместительного свойства скалярного произведения следует , поэтому достаточно доказать, что. Последнее равенство выполняется с точностью до знака, потому что обе его части с точностью до знака определяют объем параллелепипеда, построенного на векторах. Но тройки векторовиодновременно являются либо правыми, либо левыми, следовательно, знаки выраженийисовпадают. Таким образом,. Следствие доказано.

Доказанное равенство (2.33) позволяет записывать смешанное произведение трех векторов ,ипросто в виде, без указания при этом, какие два вектора (первые два или последние два) перемножаются векторно.

Следствие 2. Три вектора компланарны тогда и только тогда, когда их смешанное произведение равно нулю.

58