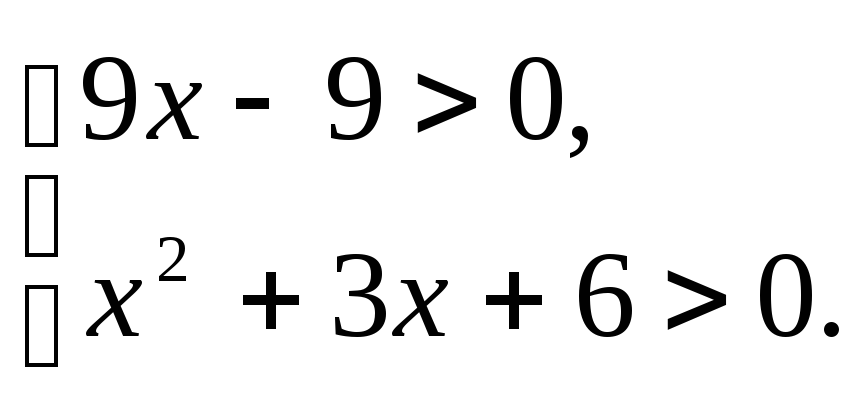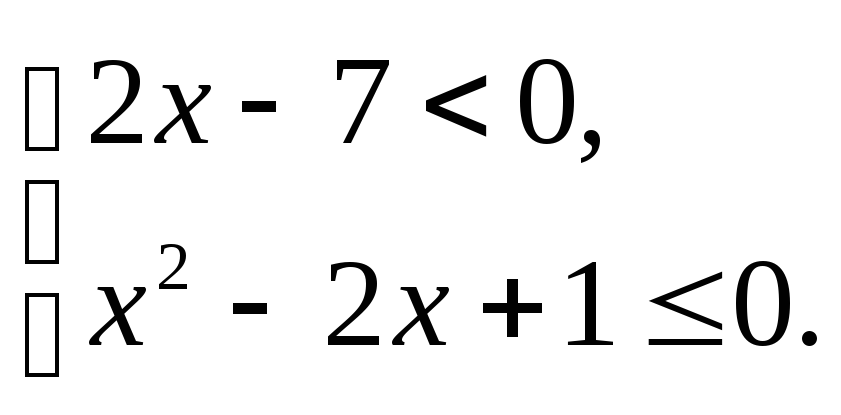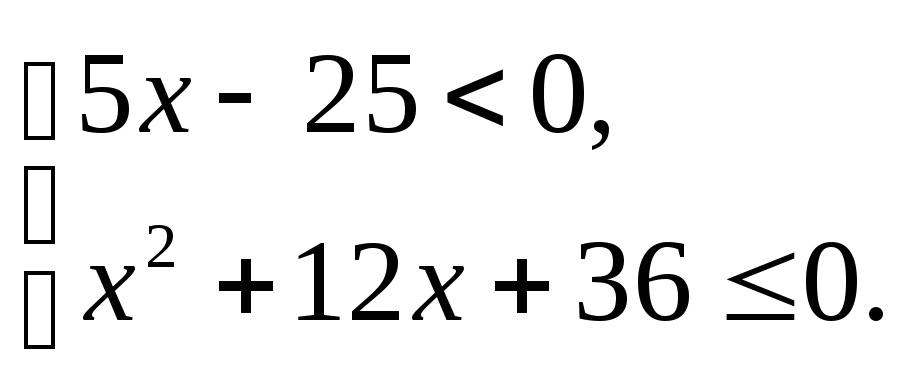7. Множества точек на плоскости, задаваемые уравнениями
и неравенствами с двумя переменными
Пусть на плоскости выбрана система координат. Тогда любое уравнение с двумя переменными F(x;y) = 0 задает множество точек на плоскости, а именно множество точекM(x;y), координатыкоторых удовлетворяют этому уравнению.
Например, точка M(– 3; 4) принадлежит множеству, заданному уравнениемx2+y2= 25, а точкаN(1; 6) не принадлежит этому множеству, так как (–3)2+ 42= 25, а 12+ 62≠ 25. В этом легко убедиться, если построить график данного уравнения в декартовой системе координат (рис. 7.1). Геометрическим местом всех точек, принадлежащих этому множеству, является окружностьR= 5 с центром в начале координат.
Рис. 7.1
Если мы рассмотрим множество, заданное в виде неравенства x2+y2< 25, то множеством будут являться все точки, находящиеся внутри этой окружности (рис.7.2). Сама окружность изображена пунктиром, чтобы показать, что точки, принадлежащие самой окружности (границе области) в данном случае на нее не попадают и точкаM(– 3; 4)множествуx2+y2< 25 (области), в чем легко убедится, а точкаN(1; 2){x2+y2< 25}.
Рис. 7.2
Если же x2+y2≤ 25, то здесь уже войдет и граница (сама окружность). Изобразим ее жирной линией (рис. 7.3).
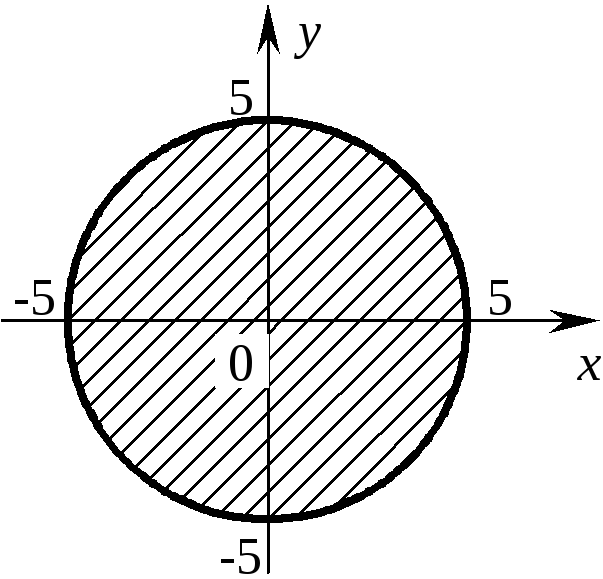
Рис. 7.3
То же касается систем линейных неравенств.
Пример.Построить область допустимых решений системы линейных неравенств.
Решение.Нумеруем ограничения задачи
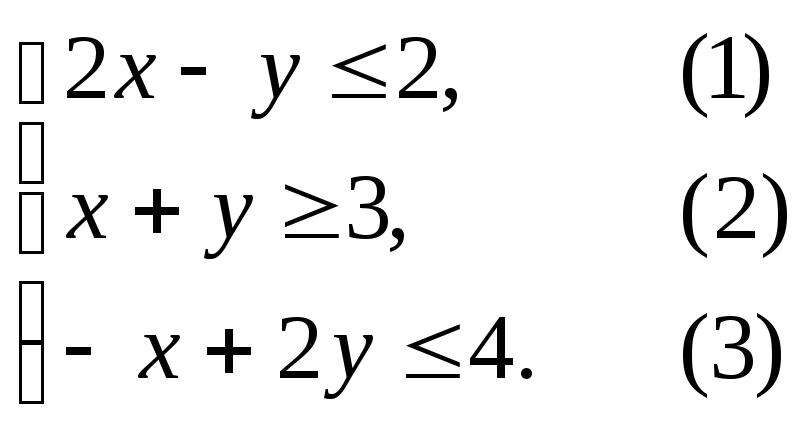
В прямоугольной декартовой системе координат (рис. 7.4) строим прямую 2x – y = 2, соответствующую ограничению (1).
Рис. 7.4
Находим, какая из двух полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решения неравенства (1). Для этого достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство. Так как прямая (1) не проходит через начало координат, подставляем координаты точки О (0, 0) в первое ограничение: 2·0 – 0 < 2. Получаем строгое неравенство 0 < 2. Следовательно, точкаОлежит в полуплоскости решений. Таким образом, стрелки на концах прямой (1) должны быть направлены в полуплоскость, содержащую точкуО.
Аналогично строим прямые x+y= 3 и –x+ 2y= 4 и области решений ограничений (2) и (3).
Находим общую часть полуплоскостей решений. Полученную область допустимых решений отмечаем на рис. 7.4 штриховкой. В этой области находятся все точки M(x;y), в которых выполняются все три неравенства системы. ◄
Задание 3
Решить неравенство (а) и систему неравенств (б).
|
3.1.а)
б)
|
3.2.а)
б)
|
|
3.3.а)
б)
|
3.4.а)
б)
|
|
3.5.а)
б)
|
3.6.а)
б)
|
|
3.7.а)
б)
|
3.8.а)
б)
|
|
3.9.а)
б)
|
3.10.а)
б)
|
|
3.11.а)
б)
|
3.12.а)
б)
|
|
3.13.а)
б)
|
3.14.а)
б)
|
|
3.15.а)
б)
|
3.16.а)
б)
|
|
3.17.а)
б) |
3.18.а)
б) |
|
3.19.а)
б)
|
3.20.а)
б)
|
|
3.21.а)
б)
|
3.22.а)
б)
|
|
3.23.а)
б)
|
3.24.а)
б)
|
|
3.25.а)
б)
|
3.26.а)
б)
|
|
3.27.а)
б)
|
3.28.а)
б)
|
|
3.29.а)
б) |
3.30.а)
б) |
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;