2. Равенство множеств. Подмножество.

Универсальное множество. Дополнение множества

Если А и В два множества, состоящие из одних и тех же элементов, и не содержат никаких других элементов, то говорят, что множества равны: А = В.

Если каждый элемент множества А является в то же время элементом множества В, то множество А называют подмножеством, или частью, множества В. Это отношение записывается так: А  В или В  А.

На рис. 2.1 дана иллюстрация этого определения с помощью так называемых диаграмм Венна (диаграмма Венна – это замкнутая линия, внутри которой расположены элементы данного множества, а снаружи – элементы, не принадлежащие этому множеству).

Рис. 2.1

Приведем примеры подмножеств:

• множество жителей Самары является подмножеством множества жителей России;

• множество всех квадратов есть подмножество множества всех прямоугольников;

• множество Z всех целых чисел есть подмножество множества R всех действительных чисел.

Если одновременно А  В, а В  А, то эти множества равны: А = В.

Отметим, что каждое непустое множество имеет, по крайней мере, два подмножества: пустое множество  и само множество.

Пусть дано какое-либо множество Е. Тогда, если рассматриваются все возможные подмножества данного множества, его называют универсальным множеством. На диаграммах Венна прямоугольник как раз и символизирует это универсальное множество.

Например, рассмотрим множество книг в университетской библиотеке. В него входят подмножества научных, художественных книг, книг по искусству и т.д. Научные в свою очередь тоже можно разбить на подмножества книг по математике, физике, химии и т.д. То есть множество всех книг – это универсальное множество, содержащее в себе различные подмножества книг.

Рассмотрим другой пример. Пусть универсальное множество Е состоит из трех элементов: {a; b; c}. Перечислим все подмножества Е: {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}, {}. Их всего 8, т.е. 2³. Не трудно доказать, что если элементов будет n, то подмножеств будет 2ⁿ.

Пусть множество А есть некоторое подмножества универсального множества Е. Тогда множество , состоящее из элементов множестваЕ, не принадлежащих множеству А, называется дополнением множества А до универсального множества Е (рис. 2.2).

Рис. 2.2

Например, если Е = {целые числа}, А = {четные числа}, то = {нечетные числа}.

3.. Операции над множествами

Суммой, или объединением, двух множеств А и В называется множество

С = А  В,

элементы которого с  С принадлежат либо А, либо В, либо принадлежат и А и В.

Данное определение можно распространить на случай произвольного конечного или бесконечного числа множеств.

На рис. 3.1 показана диаграмма Венна объединения двух (а) и трех (б) множеств.

а)б)

Рис. 3.1

►Пример 3.1.Заданы числовые множестваА= {3, 5, 7, 13} иВ= {2, 4, 5, 7, 9}. Найти множествоС=АВ. Показать решение с помощью диаграмм Венна.

Решение. Множество С состоит из всех элементов входящих в множество А или множество В. Союз «или» здесь не разделительный, то есть не исключается возможность одновременной принадлежности некоторых элементов и множеству А и множеству В. Итак,

С = А  В = {2, 3, 4, 5, 7, 9, 13}.

Изобразим С=АВс помощью диаграммы Венна (рис. 3.2). Для наглядности множества показаны вместе с элементами. ◄

Рис. 3.2

Произведением, или пересечением, двух множеств А и В называется множество

С = А  В,

элементы которого с  С принадлежат одновременно и А и В.

Данное определение также можно распространить на случай произвольного конечного или бесконечного числа множеств.

На рис. 3.3 показана диаграмма Венна пересечения двух (а) и трех (б) множеств.

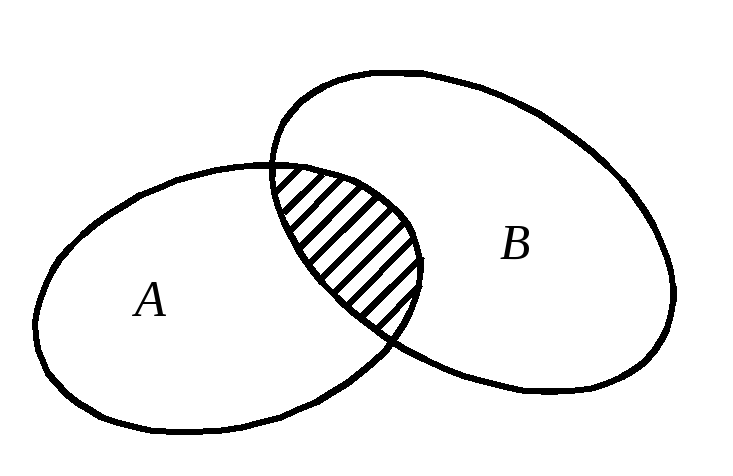
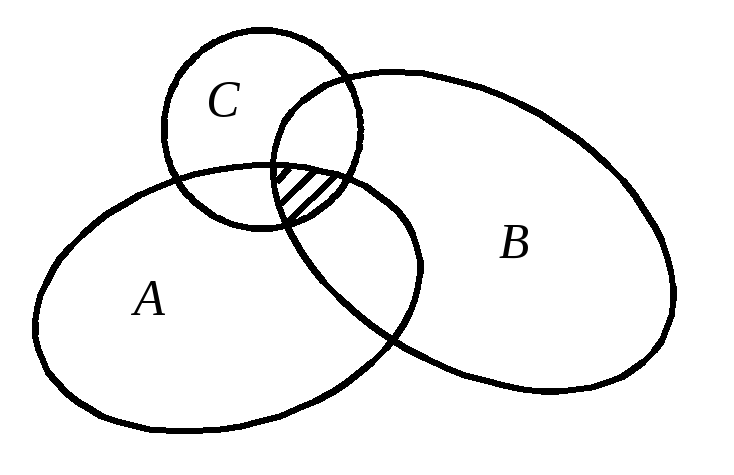
а)б)

Рис. 3.3

►Пример 3.2.По условиям примера 3.1 найти множество

С=АВ.

Решение. Множество С состоит из всех элементов входящих одновременно как в А, так и в В. Как видно из рис. 3.2 такими элементами являются 5 и 7. Следовательно

С = А  В = {5, 7}. ◄

►Пример 3.3. Пусть А = {1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72} – множество натуральных делителей числа 72, а В = {1, 2, 3, 6, 9, 18, 27, 54} – множество натуральных делителей числа 54. Тогда множество С = {1, 2, 3, 6, 9, 18} является пересечением множеств А и В, а числа, входящие в множество С, являются делителями для 72 и 54. Наибольший элемент множества С, то есть 18, называется наибольшим общим делителем чисел 54 и 72. ◄

Следует отметить, что пересечение нескольких непустых множеств может быть пустым множеством.

Термин «пересечение» по существу геометрического происхождения. Например, если прямая и плоскость не параллельны, то их пересечением является точка.

Разностью двух множеств А и В называется множество

С = А\В,

состоящее из элементов, принадлежащих множеству А, но не принадлежащих множествуВ.

Разность между множеством А и множеством В часто называется дополнением множества В до множества А.

►Пример 3.4. Пусть заданы множества А = {3, 5, 7, 13} и В = {2, 4, 5, 7, 9}. Тогда разности этих множеств будут иметь вид:

А\В = {3, 13} – элементы А, не входящие в В (рис. 3.4а);

В\А = {2, 4, 9} – элементы В, не входящие в А (рис. 3.4б). ◄

а)б)

Рис. 3.4