6. Числовые множества. Множества точек на прямой, задаваемые алгебраическими уравнениями и неравенствами

В математике важную роль играют множества, составленные из «математических» объектов – чисел, точек, геометрических фигур и т.д. Примерами числовых множеств являются:

• множество всех действительных чисел R;

• множество всех рациональных чисел Q;

• множество всех натуральных чисел N;

• множество всех целых чисел Z;

• множество всех иррациональных чисел L.

Рассмотрим основные понятия, характеризующие множество точек на прямой.

1. Интервалы.Еслиaиbдва действительных числа иa<b, то множество всех чиселx, удовлетворяющих неравенствуa<x<b, называетсяоткрытым интервалом(числовым промежутком) и обозначается (a,b). Сюда же относятся интервалы (– ∞; + ∞), (– ∞;a), (b; + ∞).

Открытый интервал не имеет ни наименьшего, ни наибольшего числа: какое бы число x  (a; b) мы не взяли, обязательно на этом интервале найдутся такие x΄ и x˝, что x΄ > x, x˝ < x. Множество всех точек любого интервала является бесконечным. На числовой прямой открытые интервалы изображаются следующим образом:

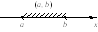
Замкнутый интервал (числовой отрезок) [a; b] состоит из всех чисел x, для которых a ≤ x ≤ b, или [a; b] = (a; b)  {a}  {b}. На числовой прямой замкнутые интервалы изображаются следующим образом:

Интервалы смешанного типа состоят из всех чисел x, для которых:

a ≤ x < b, или [a, b) = (a, b)  {a};

a < x ≤ b, или (a, b] = (a, b)  {b};

∞ < x ≤ a, или (– ∞, a] = (– ∞, a)  {a};

b ≤ x < + ∞, или [b, + ∞) = (b, + ∞)  {b}.

На числовой прямой смешанные интервалы изображаются следующим образом:

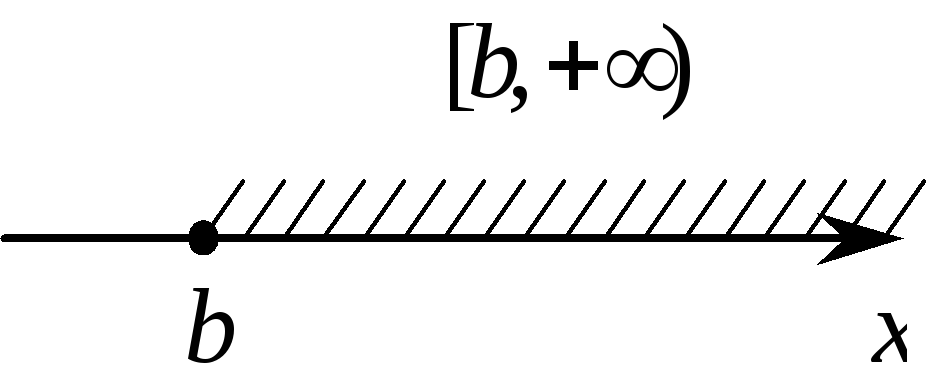
2. Окрестность точки. Окрестностью точки х₀ называется любой открытый интервал, содержащий эту точку. Возьмем какое-либо положительное число ε. ε-окрестностью точки х₀ называется открытый интервал с центром в точке х₀ и длиной 2ε, то есть интервал (х₀ – ε; х₀ + ε).

3. Множества точек, задаваемых алгебраическими уравнениями и неравенствами. С каждым уравнением связаны два числовых множества. Первое из них –область определения уравнения. Это множество состоит из всех значенийx, для которых имеют смысл обе части уравнения. Второе множество – этомножество корней уравнения, то есть чисел, при подстановке которых в уравнение, оно обращается в тождество.

►Пример 6.1. Областью определения уравнения

= 2 – x

является множество [- 4; + ∞), так как x + 4 ≥ 0, x ≥ 4.

Найдем корни уравнения. Возведем обе части в квадрат

x + 4 = (2 – x)²; x² – 5x = 0; х·(х – 5) = 0;

х₁ = 0; х₂ = 5.

Оба числа х₁ = 0 и х₂ = 5 принадлежат множеству [- 4; + ∞), однако число х₂ = 5 является посторонним корнем уравнения (это показывает простая проверка: ≠ 2 – 5). Таким образом, множество корней данного уравнения {0} [- 4; + ∞). На числовой прямой эти множества изображаются так:

Те же рассуждения относятся и к алгебраическим неравенствам.

Пример 6.2. Решить систему неравенств

Первое неравенство х – 2 ≤ 0 имеет множество решений х ≤ 2, или х  (– ∞; 2]:

Во втором неравенстве находим корни:

х² – 5х – 6 = 0; х₁ = – 1, х₂ = 6.

Решением его будет интервал х(– 1; 6):

Чтобы получить решение системы неравенств, нужно найти пересечение множеств (– ∞; 2]  (– 1; 6). Покажем эти множества на числовой прямой:

Как видно из рисунка, пересечением является интервал смешанного типа х(– 1; 2], на котором штриховки накладываются друг на друга. ◄