Konspekt_za_2y_semestr_po_fizike

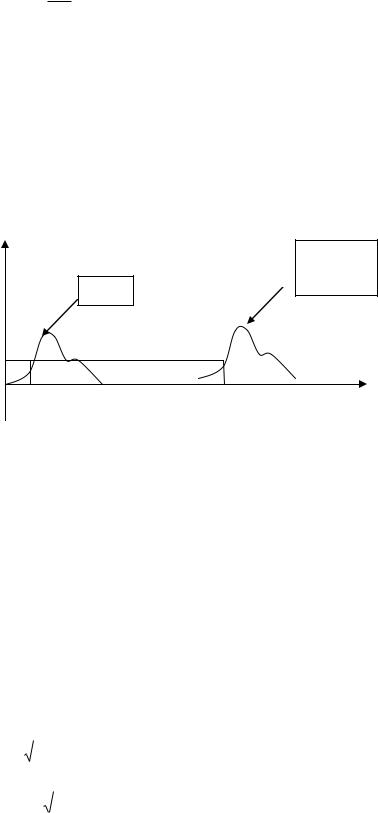
f v 2 2t 0t x 2

Решение этого уравнения будем искать в виде функции f (x vt)

Подставим эту функцию в наше уравнение: v 2 f ``v 2 f `` 0

И убеждаемся , что она является решением.-

f

t 0

f (x vt)

t 0

противоположную сторону. f (x) -волновая функция.

Общее решение уравнения будет: f (x,t) f1 (x vt) f 2 (x vt) Рассмотрим трёхмерный случай.

2 f v 2 2 f 0t 2

Рассмотрим сферически симметрическое решение: f (R, t)

f (R, t) f (x, y, z, t) f (R, t)

f (R, t) -сферически-симметрическое решение

В этом случае волновое уравнение удобно переписать x, y, z R

21

Тогда волновое уравнение будет иметь вид:

Получим одномерное волновое уравнение, решение которого уже найдено:

(R vt)

f (R, t) R1 * (R vt)

f

1

R

описывает возмущение которое возникает из ничего на бесконечности и растёт при

22

приближение к центру. Такое решение физически невозможно. Поэтому в сферически

§2.2 Гармонические волны.

Рассмотрим волновую функцию вида: f (R , t) A cos(t KR) , const -циклическая

частота волны. K const -волновой вектор.

t KR (R, t) -фаза волны

A амплитуда волны

Функция f (R, t) называется гармонической или монохроматической волной.

Для того чтобы рассмотренная функция являлась решением волнового уравнения:

дисперсионным.

Для того чтобы получить это уравнение в нашем случае подставим гармоническую

Решая это уравнение мы можем найти частоту как функцию K

W (K )

Полученное решение называется дисперсионным соотношением. Точки в пространстве фазы которых одинаковы.

const образуют поверхность которая называется волновой или волновым фронтом. Как известно градиент любой функции направлен к поверхности на которой она постоянна.

Так как вектор К постоянен по величине и направлению, то волновая поверхность будет плоской. Поэтому данная гармоническая волна называется плоской гармонической

волной. При этом направление распространение волны будет совпадать с

направлением K .

K X

23

K * R kx

K x K

K y K z 0

Расстояние на котором фаза волны меняется на 2 называется длинной волны

t K(x ) (t kx) 2

Скорость с которой движется точка в пространстве где фаза волны постоянна называется фазой скоростью волны. Для определения этой скорости продифференцируем по времени условия постоянной фазы

t Kx const

K dxdt 0

v p dx dt K

Следует заметить, что фазовая скорость это не скорость математической точки

поэтому фазовая скорость может быть любой, то есть и больше скорости света.

Если фазовая скорость постоянна , то есть не зависит от , K , то говорят что нет дисперсии..

у такой волны волновой фронтсферическая поверхность. K в каждой точке волнового фронта направлен к нему, то есть по радиусу. Все остальное также как у плоской волны.

§2.3 Распространение волны в ограниченной среде. Стоячие волны

Рассмотренный одномерный случай в §2.1 было показано, что :

f (x,t) F1 (x vt) f2 (x vt)

Рассмотрим среду одномерно ограниченную с одной стороны в точке х=0 с нулевым граничным условием:

f (0,t) 0

24

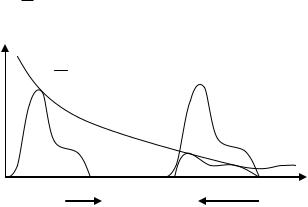
f

v

х

Пусть в такой среде распространяется волна. Из нулевого граничного условия следует что: f (0,t) f1 (vt) f2 (vt) 0

f1 ( vt) f2 (vt)

f (x,t) f2 (x vt) f2 (vt x)

f

f 2 (x vt)

0

х

x

x

Таким образом при рассмотрение волны в ограниченной среде происходит изменение направления распределения на границе среды. Такое явление называется отражением.

25

Изменение знака волновой функции в рассмотренном примере связанно исключительно с видом граничного условия.

Рассмотрим гармоническую волну которая распространяется в ограниченной сфере с нулевым граничным условием f (0,t) 0

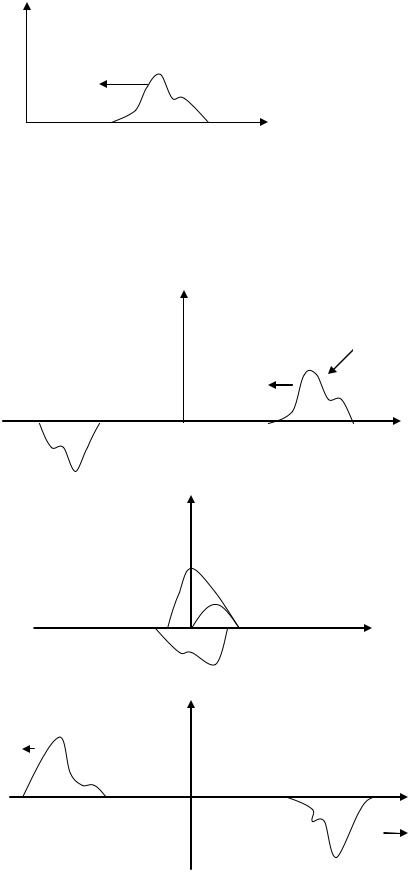
f (x,t) Acos(t Kx) Acos(t Kx) 2Asin(Kx)sin(t) 2Asin Kx sin t

f

х

То есть в рассмотренном случаи гармонические возмущения в ограниченной среде никакого распространения волны наблюдаться не будет.

Каждая точка среды будет совершать гармонические колебания с частотой и постоянной амплитудой величина которой определяется координатами точки 2Asin Kx . Полученное возмущение называется стоячей волной.

Точки в которых амплитуда колебаний равна нулю называются узлами стоячей волны,

Am ax пучность

При переходе через узел в стоячей волне фаза колебаний меняется на . Если среда ограничена с двух сторон нулевыми граничными условиями.

f (0,t) f (L,t) 0 тогда: f (x, t) 2 Asin Kx sin t

f (L, t) 2Asin KL * sin t 0 sin KL 0

KL n N 1,2,3

26

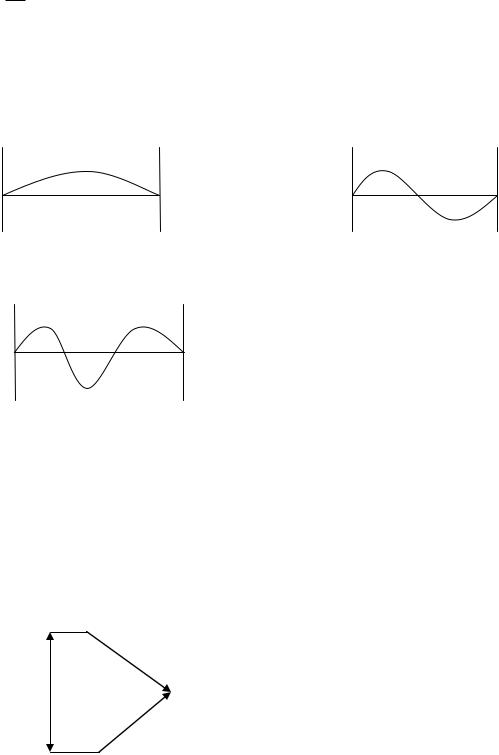
2 L n L 2 n

n=1

n=2

n=3

Полученные решение называется собственным модулями колебаний.

Заметим, что в полностью ограниченной среде возможны стоячие волны(собственные моды )лишь с определённой длиной волны (частотой) которая меняется дискретно.

§2.4 Интерференция волн двух источников .

Рассмотрим два точечных источника которые излучают сферически симметричные гармонические волны с одинаковой частотой

R1

P

d

R2

Определим волновую функцию в точке p. Так как волновое уравнение линейно то волновая функция в точку p линейна .

Сначала рассмотрим случай когда фазы колебаний источников одинаковы. Решить задачу в общем случае достаточно сложно. Поэтому рассмотрим приближение, когда точка p находится на большом расстояние от источника настолько большом , что можно считать, что амплитуда колебаний каждого источника одинаковы.

27

A0 A0 A(R) R1 R2

R1 || R2

Выясним условия применимости такого приближения

d 2 L22 L12 (L2 L1 )(L2 L1 )

L2 L1 L

d 2 L2 L1

2L

L2 L1 0 (при выполнение нашего условия)

L2 L1 2

d 2 2L 2

L d 2

Если выполнить это условие то говорят, что можно пользоваться приближение далекого поля или волновой зоной.

Большое

расстояние

Мы будем наблюдать гармоническую волновую функцию амплитуда которой будет:

A( ) 2 Acos K (R1 R2 ) 2

R1 R2 d sin - геометрическая разность хода Условия максимальной амплитуды.

28

То есть геометрическая разность хода равна целому числу длин волн. Условие минимальных амплитуд

d sin 2 (2m 1)

Геометрическая разность хода равна нечетному числу длин полуволн.

Q

d

Рассмотрим более общий случай, когда два источника излучаю волны с различными начальными фазами.

Определим угловое расстояние между двумя ближними максимумами. Условие максимума nго порядка:

Kd sin 1 n 2

Условие максимума n+1

Kd sin 2 (n 1) 2

29

Рассмотрим случай когда источники расположены далеко друг от друга d>> , тогда угловое расстояние между ближайшими максимумами

будет <<1 d

В § 1.3 было показано, что энергия колебаний пропорциональна A2 поэтому энергия излучения двух источников будет пропорциональна A2 A(R, t) , так как угловое

расстояние между ближайшем максимум при d мало то на не большом участке поверхности dS будет расположено большое количеством max и min амплитуд.

A2

dS

A2 m

A2 m

2

Поэтому средние значение энергии излучение на единицу площади поверхности будет

Рассмотрим близко расположенные источника d<<1

30