
Konspekt_za_2y_semestr_po_fizike
.pdf
Лучом называют линию касательно к каждой точке которой является вектор К. Для определения формы луча очень полезен принцип Ферма для вывода которого рассмотрим разности фаз в двух точка распространяется на одном луче в один и тот же момент времени.
Эту разницу фаз модно вычислить интегрируя бесконечно малые изменения фазы вдоль луча
d |
d |
dt dR |
1 2 |
|
t |
|
|
Так как t const dt 0
aR
1 2
С другой стороны dR dl
k
То есть градиент направлен по касательной к траектории точно также как и dldR dl | | dl
Из уравнения Эйконала
v |
|
|
|
|
|
|
|
|
|
|
| | |
|
|
|
|
|
|
|
|
|
|
|
|
||||
| | |
|
|
|
|
|
v p |
|||||||
|
|
dl |
|
|
dl |
|
|
|
|||||
v |
p |
v |
p |
|
|
||||||||
|
|
|
|
|
|
||||||||
|
|
1 2 |
|
|
|
|
1 2 |
|
|
|
|||
|
|
|
|
|
v |
|
|
|
|
|
|
||
Интеграл |
|
dl |
вычислим вдоль луча и равен времени распространения волны вдоль |
||||||||||
|
|
||||||||||||
p
луча от 1 до 2.
Заметим, что разность фаз в точках 1-2 величина постоянная и не зависит от способа её нахождения. Туже самую разность фаз можно по другой траектории не совпадает с
лучом, но в этом случаи полученный результат будет неправильным так как , dl
непараллельные Выбирая каждый раз другую траекторию не совпадающий с лучом мы будем получать
различные результаты, то есть будет зависит от траектории и только тогда когда траектория совпадёт с лучом не зависит от формы траектории.
df |
0 f |
не зависит от х |
dx |
|
|
|
|
Условие независимости функции и условие её экстремума совпадает поэтому интеграл вычисленный вдоль луча не зависит от формы луча и является экстремальной. Оказывается что на траектории луча это минимальная величина.
dl min Время распределения волны вдоль луча минимально. Это и есть принцип
vp
Ферма.
Рассмотрим форму луча между двумя точками в однородной среде.
В однородной среде во всех точках фазовая скорость волны будет постоянна
|
dl |
v |
|
|
dl |
|
v |
|
p |
||||
|
|
|
||||
|
|
|
|
|
|
|
1 2 |
|
p |
|
|
1 2 |
|
51
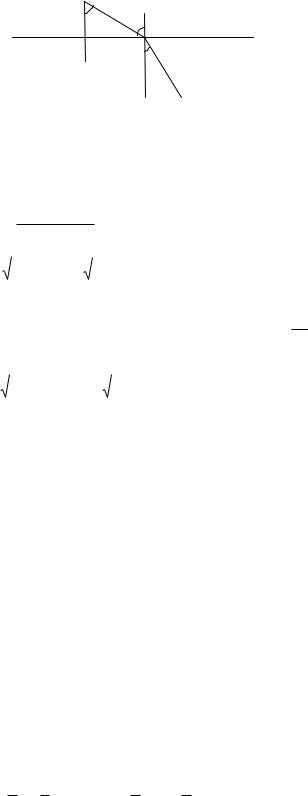
dl min -длинна луча.
1 2
Таким образом в однородной среде луч между точкой 1 и 2 должен быть минимальной длины, то есть прямая линия.
Другими словами в однородной сфере лучи это прямые линии.
Рассмотрим форму луча между точками 1 и 2 находящихся в разных однородных сферах
x
l
h2
Так как в каждой сфере луч это прямая линия то общий луч будет состоять из двух прямых.
Время распространения волны от точки 1 до точки 2 будет
t |
l1 |
|
l2 |
|
vp1 |
vp2 |
|||
|
|
l2 
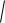 h2 2 (l x)
h2 2 (l x)
t |
|
h 2 |
x 2 |
|
|
h 2 |
(l x) |
|
|
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
|
|
v p1 |
|
|
|
v p 2 |
|
||
Так как время должно быть минимальным то dxdt 0
1 |
|
|
|
|
|
|
|
x |
|
|
|
|
e x |
|
|
0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
v p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
x |
2 |
v p 2 |
2 |
(e x) |
2 |
||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
h1 |
|
|
|
|
|
h2 |
|
|
|
|||||||
|
sin |
|
|
|
v p1 |
|
|
|
|
|
|
|
|
|
|||||||
|
sin |
|
|
v p 2 |
|
|
|
|
|
|
|
|
|
||||||||
n- коэффициент преломления. |
|
|
|
||||||||||||||||||
n |
c |
|
|
|
для электромагнитных волн |
||||||||||||||||
v p |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
sin |
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
||||
|
sin |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
§2.13 Электромагнитные волны в вакууме.
Электромагнитное поле, как известно полностью описывает уравнение Максвелла которые в вакууме будут иметь вид
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
j |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
E |
0 |
|
|
|
|
|
|
|
B |
0 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
1 |
E |
|||||||||
xE |
|
|
xB |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
c2 t |
|||||||||||||||||||
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
E |
) |
|
|
|
||||||
x(xB |
) x( |
|
|
|
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
c 2 t |
|
|
|
|||||||||
(B ) B () (B ) 2 B
52

( |
|
|
) 2 |
|
|
|
1 |
|
|
|
|
|
|
||||||||||
B |
B |
xE |
|
||||||||||||||||||||
|
|
c2 |
|
|
t |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1 2 |
B |
|
|
|
|
|
|
|
||||||
|
2 B |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
c 2 t 2 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2 |
B c 2 2 B 0 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Уравнение для |
|
|
совпадает с волновым уравнением решение которого было найдено в |
||||||||||||||||||||
B |
|||||||||||||||||||||||
§ 2.1. Точно также:
x(xE ) x( Bt ) (E ) 2 E t (xB )
2 E 2 |
|
1 2 E |
||
c 2 |
t 2 |
|||
|
|
|||
2 E c 2 2 E 0t 2
То есть мы получим волновое уравнение. Таким образом решение уравнения Максвелла в вакууме будет иметь вид волновых функций. Для простоты рассмотрим сначала случай гармонических волн.
E Eo ei ( t kR )
B B0 ei( t kR )
То есть мы ищем решение уравнения Максвелла в виде плоских монохроматических волн.
Подставим решение в уравнение Максвелла при этом учтём, что оператор можно
заменить на
R
E 0 ikE 0 k EB 0 ikB 0 K B
xE Bt
iKxE i E B
xB 1 E c 2 t
ikxB ci2 E
kxB c 2 E
53

KE B
E E k B
E BC
K
B
§ 2.14 Энергия электромагнитного поля. Вектор Умова-Пойтинга
Рассеем некоторый замкнутый объём V ограниченно замкнутой поверхности S в котором существует электромагнитное поле.
Предположим, что это поле обладает энергией плотность которой u. Тогда полная энергия электромагнитного поля будет udv
v
Вычислим t v udv .
Изменение энергии в объёме V может происходить по двум причинам: за счёт переноса энергии через поверхность S и за счёт мощности всех сил действующих в системе. Смотри §2.4. Для вычисления переносим через поверхность S, введём вектор uv , где v скорость переноса энергии, которая называется плотностью потока энергии.
Тогда энергия переноса в единицу времени, через ds, будет uvds (смотри Электроток.
Уравнение непрерывности). Так как это будет энергия, выносим из объёма ds направленная наружу, то за единицу времени энергия в объёме уменьшится на величину
- uvds .
s
Если внутри объема V имеются электромагнитные заряды, то электронное поле будет совершать работу, что приведёт к уменьшению энергии поля (работа магнитного поля равна 0)
В § « Законы электрического тока» было показано, что мощность электромагнитных сил в единицу объёма вещества будет jE поэтому за единицу времени энергия
электромагнитного поля в объёме V уменьшится на величину - jEdv
v
udv uvds |
|
|
|
|
|
|
|||
jEdv |
|||||||||
v |
t |
s |
v |
||||||
|
|||||||||
u dv (uv )dv |
|
jEdv |
|||||||
|
|||||||||
v |
t |
v |
|
|
|
v |
|||
|
|
|
|
||||||
Так как это равенство должно выполняться для любого объекта V
u (uv ) jEt
Рассмотрим уравнение Максвелла в сфере.
54
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
B 0 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
1 |
|
E |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
B |
|
|
|
|
|
xB |
|
|
|
|
|
|
t |
||||||||||||||
|
|
|
|
|
|
|
c 2 |
c 2 |
||||||||||||||||||||
xE |
|
|
|
0 |
||||||||||||||||||||||||
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
jE ( |
|
|
E |
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
0 |
0 |
xB |
) * E |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рассмотрим (ExB )
(ExB ) E (ExB ) B (ExB ) B (xE ) E (xB )
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
E |
|
|
|
|
|
|
|
|
|
|
B |
|
1 |
|
E |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
jE |
|
|
|
|
c 2 (ExB) |
|
|
c 2 |
B |
|
|
|
|||||||||||||||||||||
2 |
0 t |
|
0 |
0 |
|
t |
2 |
0 t |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
c 2 |
|
2 ) |
C 2 |
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
||||
|
|
|
|
0 E |
0 |
|
(ExB ) |
(u * v ) |
||||||||||||||||||||||||||
|
|
|
|
( |
|
|
B |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
t |
|
|
2 |
|
|
|
2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
0 c 2 B 2 0 c 2 (ExB ) 2 t
Сравнивая полученное выражения, находим, что плотность энергии электромагнитного
поля будет |
|
|
|
|
|
||||||
u |
|
0 |
E 2 |
|
|
0 |
c2 B 2 |
||||
|
|
|
|
|
|||||||
|
2 |
|
|
|
2 |
||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Вектор Умова-Пойтинга |
||
|
S |
|
0 |
c2 |
ExB |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Для того чтобы убедится, что полученные результаты верны вспомни §2.13, что
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Bc E , u 0 E 2 |
тогда |
S |
0 c 2 |
E |
xB |
||||||||||||||
(v p ) с |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
0 |
c | ExB | v |
p |
|
0 |
E 2 v |
uv |
p |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Таким образом электромагнитное поле обладает энергией, плотность которой
u 0 E 2 0 c 2 B 2
2 2
Часть 4 Квантовая механика.
§1 Экспериментальные основы квантовой механики.
К началу 20го века основные физические явления были объяснены классической физикой за исключение нескольких явлений:
1) тепловое излучение тела. Как известно любая движущаяся с ускорением заряженная частица излучает электромагнитные волны. Так как все тела содержат заряженные частицы, то при температуре выше абсолютного 0 они двигаются. Поэтому любое тело при T>0 излучает электромагнитные волны частота которых от 0 до
Пусть энергия излучает электромагнитные волны за единицу времени приходящаяся на
единицу поверхности в интервале частот от до d будет |
I ( )d |
|
I ( ) спектральная |
плотность |
излучения. |
С помощью классической электродинамики Максвелла можно получить зависимость
I ( )
55
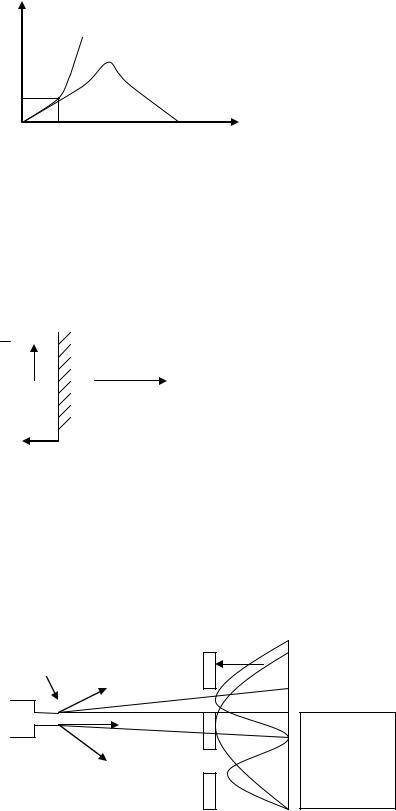
I ( )
~ 2
I ( )
d |
|
I () ~ w2 -закон Релея и Джинкса или «ультрафиолетовой катастрофой»
2) Фотоэффект, который состоял в том, что электромагнитная волна вырывала с поверхности проводника электромагнит. Само это явление легко объясняется классической электродинамикой. Под действие электромагнитного поля электроны проводника начинают двигаться вдоль поверхности.
E |
k |
|
qvxB
A на движение электронов со стороны qvB со стороны магнитного поля направленного
наружу и она приводит к выражению.
Столетов экспериментом установил, что увеличение амплитуды волны то есть энергии волны, скорость вылетевших электронов не меняется, а меняется их число, что невозможно объяснить классической физикой.
3) Опыты по дифракции электрона
1. Опыт с пулями
Пулемет
Мишень
Будем описывать попадание пуль в мишень вероятность попадания P. Если открыть оба отверстия то вероятности попадания складываются.
56

2. Опыт с волнами
A2
Если открыть одно отверстие то (§2.6) будем наблюдать дифракцию, если второедифракцию
Если оба то интерференцию 3. Опыт с электронами
p
p- вероятность попадания в мишень.
Вероятности не складываются, а интерферируются Электроны описывают вероятности как пули, а вероятности интерферируются как у
волн.
57

§2 Волны де Бройля
Так как электрон проявляет одновременно волновые и корпускулярные свойства, то возникла идея, что этим обладают и все остальные частицы и поэтому общие законы механическим частицам и механические волны должны совпадать.
В теории волны таким общим законом является принцип Ферма, которой позволяет
описывать траектории луча из условий минимума dl v p
Оказывается, что такой же принцип существует и в классической механике 
 E udl
E udl
должен быть min
Очевидно, что объединив свойства траектории луча и траектории частицы это одно и тоже, поэтому оба принципа должны удовлетворятся одновременно
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
E u |
|
|
|
|
|
|
||||||||||||||||||||||
Vp |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
С другой стороны скорость частицы |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
v |
|
|
|
|
2(E u) |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
V |
|
|
|
|
d |
|
групповая скорость волн. |
|
|||||||||||||||||||||||
g |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
dk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
v |
|
|
|
vg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
m |
|
|
|
dk |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2(E u) |
d |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
Vp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
K |
|
E u |
|
|
|
|
|
|
||||||||||||||||||||||
|
Vp |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
dE |
|
|||
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
E u |
|
( ) |
|
|
|
|||||||||||||||||
|
|
|
2(E u) |
|
|
|
d |
2 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
E u |
|
|||||||||||||||||||||||
Так как это равенство должно выполняться для любых E и u то коэффициенты (E,u) в левой и правой частях должны быть равны.
d |
( ) 0 |
const |
|||||||
d |
|||||||||
|
|
|
|
|
dE |
|
|||
|
|
|
|
dE |
|
const |
|||
|
m |
|
|
||||||
|
|
|
d |
||||||
|
|
|
|
||||||
|
|
|
|
|
|||||
|
2 |
2 d |
|
||||||
|
|
|
|
|
|||||
dE постоянная Планка d
2h
Интегрируя получим
E E0 |
E0 произвольная постоянная величина |
Так как если частицы нет то E 0 и 0 то очевидно, что E0 0
58
|
E |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
m |
|
|
|
|
|
|
|
|
|||||||
2 |
2 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2m |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
k |
|
|
2m(E u) |
|
|
|
E u |
|
|
|
|||||||||||||
|
|
|
|
|
|
||||||||||||
|
v p |
|
|
|
|
|
|
|
|
|
|
|
|
||||
k p |
|
|
|
|
|
|
|
|
p mv |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
p k |
|
|
|
|
|
|
|
|
|
|
||||||
Таким образом, частица с одной стороны характеризует корпускулярные
|
|
|
|
|
|
|
|
характеристики E и |
p , а с другой стороны волновыми и k |
которые связаны |
|||||
соотношением |
|
|
|
|
|
||
|
|
|
|
||||
E |
p |
K |
|
||||
Так как k |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||
hp - длина волны Дебройля
Таким образов каждая частица соответствует некоторая волновая функция.
(R , t) Aei (kR t )
|
|
|
p k |
E |
|
Получим волновую функция называемую волной Дебройля.
§ 3 Уравнение Шредингера.
Как было показано в § 2.1 волновая функция является решением волнового уравнения, поэтому для волновой функции Дебройля мы можем написать точно такое же уравнение
как |
2 |
v p 2 0 , где v p - фазовая скорость волны. |
|
t 2 |
|
Рассмотрим волновые функции в виде монохроматической волны, то есть с постоянной частотой
E
Тогда волновая функция:
(R , t) Aei (kR t ) (R )e i t
Подставим функцию в уравнение
59

2 ( |
|
)ei t v |
2 e i t 2 ( |
|
) 0 |
|||||||||||||||||
R |
R |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
||
|
2 ( |
|
) v2 2 ( |
|
) 0 |
|
|
|
|
|
||||||||||||
R |
R |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
v2 |
|
2 |
|
|
2 |
|
2 2 |
|
|
|
|
2 2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
p |
|
|
K 2 |
|
|
|
2 k 2 |
|
|
|
p2 |
|
|
2m(E u) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2 |
|
2 2 2 |
0 |
|
|
|
|
|
|||||||||||||
2m(E u) |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 (R ) (E u) (R ) 0 |
||||||||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
||||||||||||||||||||
2m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Это уравнение Шредингера для независимой от времени части волновой функции частицы (R) и часто называют стационарным уравнение Шредингера.
Умножим это уравнение на e i t
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 (R , t) E (R, t) u (R, t) 0 |
||||||||
|
|
|||||||||
|
2m |
|
|
|
|
|
|
|
|
|
(R, t) (R)ei t |
|
|||||||||
|
i |
iE |
E i |
|
||||||
|
|
t |
||||||||
|
t |
|
|
|
|
|
|
|||
|
|
|
2 |
|
||||||
i t |
|
|
2 u 0 |
|
||||||
2m |
|
|||||||||
Полученное уравнение называется уравнение Шредингера . Рассмотрим комплексно сопряженное уравнении.
(a ib)* a ib
(a ib)(a ib) a2 b2 | a ib |2 (a ib)(a ib)*
Рассмотрим уравнение Шредингера и комплексно сопряжённое уравнение Шредингера
|
|
2 |
|
i t |
|
|
2 u 0 |
2m |
|||
|
|
* |
|
|
2 |
|
|
|
|
|
|
|
|
||||
i |
|
|
t |
|
|
2 * u * 0 |
|
|
|
||||||||
|
|
2m |
|
|
|
||||||||||||
i ( |
* |
|
|
|
* |
2 |
* |
|
* |
) 0 |
|||||||
t |
|
t |
) |
2m ( |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
||||
i |
|
|
( |
* ) |
2 |
( * * ) 0 |
|
|
|||||||||
|
|
|
|
|
|
||||||||||||
|
t |
|
|
|
|
2m |
|
|
|
|
|
|
|
|
|||
Действительно
( * * ) * * 2 * *
|
( * ) |
|
( *) 0 |
|
t |
2mi |
|||
|
|
Напоминает по внешнему виду уравнение непрерывности.
(v ) 0t
Чтобы убедиться в этом рассмотрим волновую функцию в виде плоской монохроматической волны Aei(kR t ) F (t)eikR
60
