
Konspekt_za_2y_semestr_po_fizike
.pdf
A(R, ) 2 Acos kd sin 2
2k d 2K
Kd 2
Тогда A(R, ) 2Acos 2
1 случай 0
A(R,t) 2A
I A2 (R, ) 4A2 4I1
2 случай
A(R, ) 0 I 2 0
§ 2.5 Многолучевая интерференция.
Рассмотри N источников которые излучают сферические волны с одинаковой амплитудой: A, , K ,0 0
Рассмотрим между источниками d.
Определим волновую функцию в точке p находящеюся в волновой зоне.
|
|
Большое расстояние |
|
|
p |
|
|
R1 |
|
d |
R2 |
|
d |
R3 |
|
d |
|
При этом учтём |
A0 |
A |
|
R |
|
f (R,t) Acos( t KR1 ) Acos( t KR2 ) .. Acos( t KRn )
Re Aei( t KR1 ) Aei( t KR2 ) .. ARe ei( t KR1 ) (1 eiK ( R1 R2 ) .. )
R1 R2 d sin
f (r,t) ARe ei( t kR) (1 e ikd sin e 2ikd sin .. e (n 1)ikd sin
31

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
inkd sin |
|
|
|
|
inkd sin |
|
|
inkd sin |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
nKd sin |
1 |
e |
2 |
|
|
e |
2 |
e |
|
2 |
|
|
||||||||||
f (R, t) Areei ( t KR1 ) |
|
|
|
|
|
A Re ei ( t KR1 ) |
|
|
* |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
ikd sin |
|
|
|
ikd sin |
|
|
|
|
|
|
ikd sin |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
1 |
|
|
|
|
ikd sin |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
2 |
|
|
e |
2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
Nkd sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
A |
|
2 |
|
|
|
|
|
Rei( t kRs ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
sin |
kd sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Rs |
|
R1 Rn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
Nkd sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
f (R, t) A |
|
|
|
2 |
|
|
|
|
|
* cos(t |
kRs ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
sin |
kd sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В точке p мы будем наблюдать волновую функцию с амплитудой
sin Nkd sin
A( ) a |
2 |
|
|
sin |
kd sin |
|
|
|
|
||
|
|
|
|
|
2 |
|
|
Рассмотрим случай когда 0 Вычислим придел этой функции по, Лопиталю находим что A(0) AN . Точно также мы можем определить амплитуду волновой функции когда
kd sin n
2
d sin 2k n n A( ) AN A(0)
При таких будут наблюдаться max амплитуды, которые называются главными. Если
Nkd sin |
m |
|
|
|
|
|
m 1, 2... кроме N, 2N ….. |
|||||||
|
|
|
|
|
|
|
|
|||||||
2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d sin |
|
2 |
* |
m |
|
m |
условие минимума. |
|||||||
|
|
|
|
|
||||||||||
|
|
|
|
K |
|
n |
|
|
|
|
N |
|
|
|
Если |
Nkd sin |
|
|
|
(2l 1) |
l 1, 2 условие побочных максимумов. |
||||||||
|
|
|||||||||||||
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
32
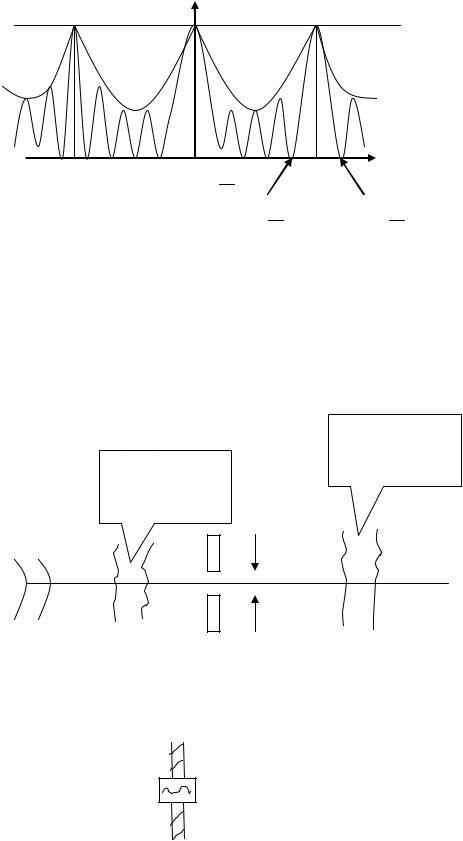
Следует заметить, что А побочных максимумов неодинакова в отличии от главных
А2
|
|
0 |
|
|
d sin |
|
|
N |
N |
|
|
|
|
|
|
|
|
|
||
|
|
N |
|
N |
||
§2.6 Дифракция, принцип Гюйгенса
Рассмотрим точечный источник излучения S от которого распространяются сферические волны и которые находиться на большом расстояние от экрана с отверстием
. Величина отверстия - D
Определим волновую функцию в точке p которая также находиться на большом расстояние от экрана , но с другой стороны.
Больное
расстояние
Больное
расстояние
d
S
*
Гюйгенс предположил, что волновая функция в точке p будет складываться из волн, функция излучения источника f s и волн функции от экрана f p f s f0
Если экран закрыть пробкой:
То волновая функция в точке p будет f s f0 |
ft -волны функции от пробки |
В результате сложения функций в точке p воловая функция будет равна 0 .
33
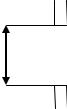
f p ft
То есть волновая функция в точке p ,будет с точностью до знака совпадать с волновой функцией излучаемой только пробкой.
Гюйгенс предположил каждую точку волнового фронта в отверстие экрана рассматривать как источник «вторичных» волн.
Волновая функция в точке p, будет равна сумме вторичных волн. Для того чтобы определить волновую функцию в точке p заметим что волновой фронт в отверстие экрана можно считать плоским так как источник находится на большом
расстояние |
от |
него. |
Разобьём поверхность волн фронта на точечные источники излучения |
|
|
D
Каждый источник излучает сферическую волну с одинаковой амплитудой, частотой и одинаковой начальной фазой которую будем считать равной нулю. Так как точка p находиться в волновой зоне то можно допустить, что амплитуда волновой функции от каждого источника одинаковы.
f ( p) Acos(t KR1 ) Acos(t KR2 ) ...
Повторяем выводы § 2.5 получаем
|
Asin |
|
|
Nkd sin |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
2 |
|
|
|
|
|
cos( t KR1 ) Для того чтобы определить амплитуду волновой |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
kd sin |
|
|
|
|
||||||||||||||||
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Asin |
Nkd sin |
|
|
|
|
|
|||||||||||
A( ) |
|
|
|
|
|
|
|
|
|
в точке 0 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||
|
sin |
kd sin |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
Воспользуемся правилом Лопиталя. |
||||||||||||||||||||||
A(0) AN |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
A(0) sin |
Nkd sin |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
A( ) |
|
|
|
2 |
|
|
|
|
|
|||||||||||||
|
|
n |
|
|
sin |
|
kd sin |
|
||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При рассмотрение |
открытой части волнового фронта мы предположим, что |
|||||||||||||||||||||
источников там очень много |
||||||||||||||||||||||
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
d 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
D Nd |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
И тогда |
|
kd sin |
|
|
|
0 |
|
и sin в знаменателе можно разложить в ряд sin x x |
||||||||||||||
2 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Тогда получаем :
34
|
|
|
A(0) sin |
|
Nkd sin |
|
sin |
kDsin |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
A( ) |
|
|
|
|
|
|
2 |
|
|
A(0) |
2 |
|
|
|
||||
|
|
|
N |
|
kd sin |
|
|
KD |
sin |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
||
Заметим, что амплитуда будет равна 0 если |
|||||||||||||||||||
|
KD sin |
n |
|
n 1, 2.... |
|||||||||||||||
|
|
|
|
|
|
||||||||||||||
2 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
То есть Dsin n - условие минимума |
|||||||||||||||||||
Если |
kDsin |
|
(2m 1) |
m 1. 2.... то мы получим условие максимума |
|||||||||||||||
|
|||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
D sin |
(2m 1) |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
|
3 |
|
2 |
Dsin0 |
|
|
|
2 |
|
||
|
|
|
|
|
|
Следует заметить, что амплитуды побочных максимумов будут значительно меньше
амплитуды центрального. |
|
Больное |
Больное |
расстояние |
расстояние |
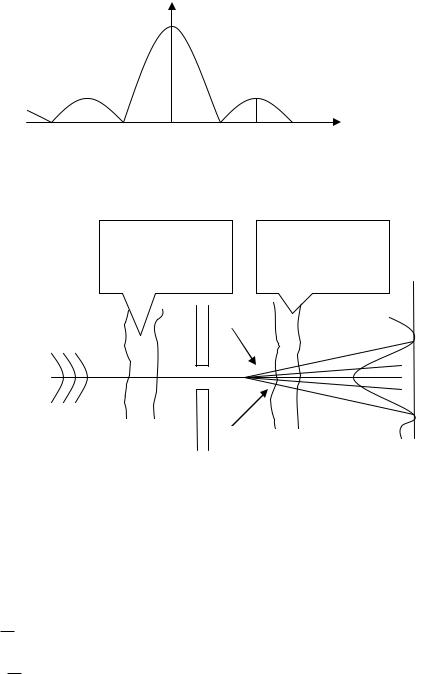
Dsin =x
- 1
|
Экран |
|
После экрана с отверстием мы будем наблюдать волну в виде расходящегося пучка. Полученный пучок излучения принято характеризовать угловой шириной или
расхождением пучка t за величину которая выберают половина углового расстояния между ближайшими к нулю нулями амплитуд.
1
sin 1
1
D
D
35
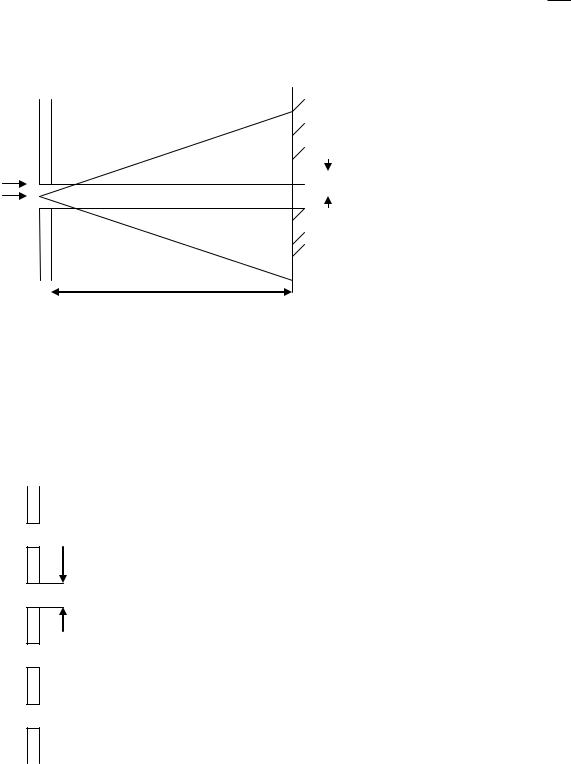
Следует заметить, что размер изображений отверстий на экране будет L * LXD и
будет значительно превышать геометрическое значение изображения отверстия .
Тень
D
D
Тень
L
Проникновения изображения в область геометрической тени называется дифракцией.
§2.7 Дифракционная решётка.
Рассмотрим экран в котором проделано N отверстий (щелей) ширина каждого из которого D
D
Дифракционная решётка
Пусть источник излучения S находиться на большом расстояние от решётки. Определим волновую функцию в точке p лежащей в волновой зоне с другой стороны решётки.
Волновая функция в точке p будет равно сумме волновых функций от каждого отверстия решётки. То есть каждая отверстие решётки мы рассмотрим как источник излучения.
f ( p) Acos(t kR1 ) Acos(t KR2 ) ...
Повторяем выводы §2.5 находим
36
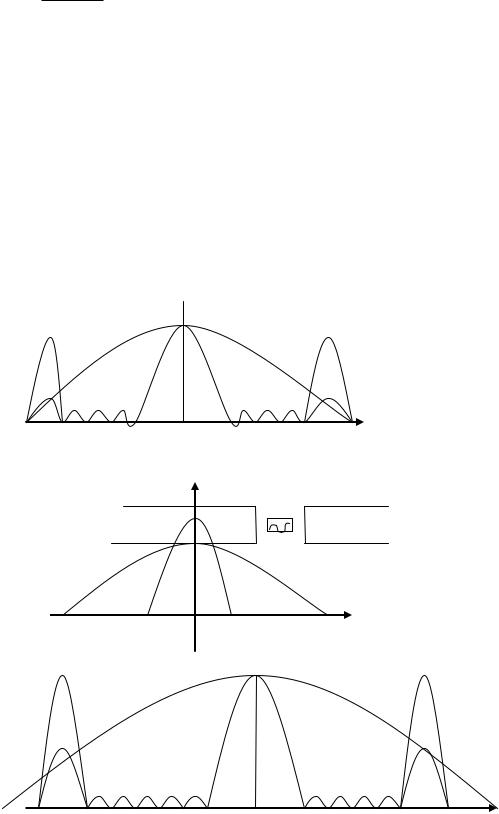
|
sin |
Nkd sin |
|
|
||
A |
|
2 |
|
|
cos( t KR) |
|
|
|
|
|
|||
sin |
kd sin |
|
||||
|
|
|
|
|
||
2 |
|
|
|
|||
|
|
|
|
|
|
|
При определение амплитуды волновой функции в точке p
Asin Nkd sin
A( p) |
2 |
|
|
sin |
kd sin |
|
|
|
|
||
|
|
|
|
|
2 |
|
|
Необходимо учесть что каждый источник имеет конечный размер D и не является точечным, как в §2.5 . Для определения амплитуды излученя такого источника надо воспользоваться результатами §2.6, где была получена амплитуда
|
A(0) sin |
kDsin |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
A( ) |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
|
kd sin |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
sin |
kDsin |
|
|
|
sin |
Nkd sin |
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||
f ( p) A(0) |
2 |
|
|
|
|
* |
|
2 |
|
|
|||||||
|
kDsin |
|
|
sin |
kd sin |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
||||
0
dsin
|
n=1 |
n=0 |
d sin n |
37
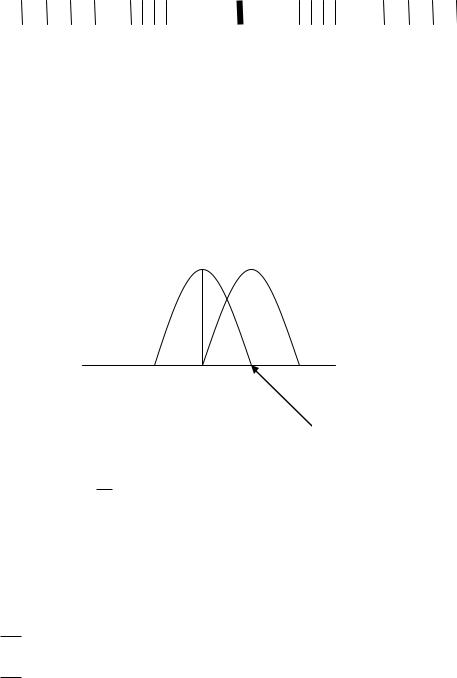
Положение главных максимумов определяет исследование d sin n n 0, 1, 2 и
зависит от длины волны излучения за исключением центрального.
Это свойство дифракционной решётки позволяет определить спектральный состав излучения. Если источник испускает волны с различной длиной то с помощью дифракционной решётки можно найти длины этих волн, так как условие главного максимума : d sin n и волны различной длины будут наблюдаться под разными углами
Максимумы первого порядка будут определять спектр первого порядка излучения. n=2 – второй порядок спектра
n=2 |
n=1 |
n=0 |
n=1 |
n=2 |
Релей предложил критерий различимости двух линий в спектре излучения линии излучения будем считать различными если главный максимум 1 совпадает с ближайшим минимумом другой 2
1
2
di sin n 1
d sin n 1 1
N
d sin n 1 1 n 2
N
n(2 1 ) 1
N
2 1 - минимальный интервал длин волн, который можно различить с помощью
дифракционной решётки.
2 1
Nn
R -разрешительная способность.
38
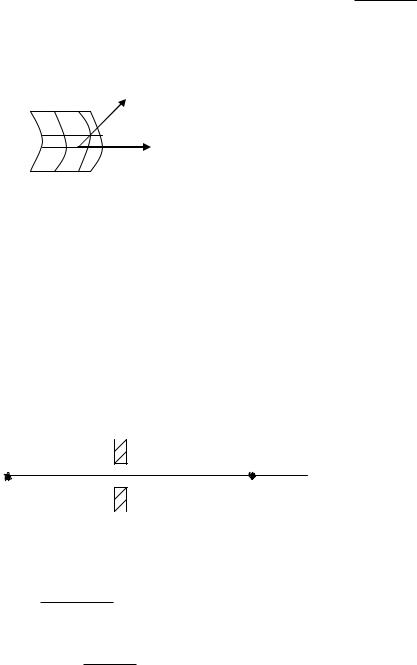
§2.8 Принцип Гюйгенса – Фринеля.
Дифракция Фринеля.
Если источник находиться на большом расстояние от экрана с отверстием, а точка наблюдения P также на большом расстояние, то наблюдается дифракция – дифракция Фраунгофера. Если нарушается хотя бы одно из условий то называется дифракция Фринеля.
Фринель дополнил принцем Гюйгенса следующим условие: для того чтобы найти волны в точке p надо разбить поверхность волнового фронта на бесконечно малые плоские участки ds. Тогда волновая функция в точке p будет равна сумме волновой функции излучаемых каждым участком.
Амплитуда в точке p будет равна сумме волны, что совпадает с принципом Гюйгенса.
Амплитуда волны излучаемая каждым участком будет
поверхности волнового фронта
n
R
P
A (n, R) ds А-амплитуда на
2
|
|
и радиуса вектора R, про который |
(n, R) - некоторые функции зависят от нормали |
n |
известно что она уменьшается с увеличением угла.
В качестве примера принципа Гюйгенса-Фринеля рассмотрим сферически симметрическую задачу когда источник, центр отверстия и точка находятся на одной прямой
S |
p |
Предположим что источник находиться на большом расстояние от отверстия. Тогда волновой фронт в отверстия будет по принципу Фринеля будет равна сумме функций излучения небольшими участками.
f ( p) Re A ei ( t KR ) ds R
Амплитуда колебаний
Тогда A( p) Re A e ikR ds R
39
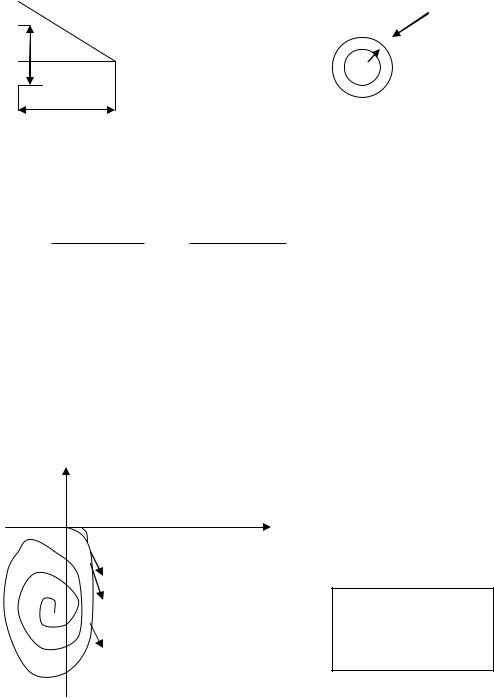
Вкачеств бесконечно малых участков поверхности ds выберем тонкое кольцо радиусом
и толщиной d
|
|
|
|
|
d |
|
R |
d |
|
|
|
|
|
|
P
R0
R2 R0 2 2
2RdR 2d ds 2d
A( p) Re a e ikR 2d Re A e ikR 2RdR R R
Re 2 e iKR dR
Таким образом амплитуда колебаний в точке p, будет пропорциональной реальной части интервала.
Rm ax
eiKR dR
R0
Для вычисления этого интеграла предположим сначала, что постоянна , тогда:
e ikR dR e ikR j dR j j
0
1
0 KR0
1 K (R0 dR) d 1 0 kdR
Таким образом предположим, что const то такой интеграл не сходится. Влияние функции приведёт к тому что каждый следующие слагаемое будет меньше
предыдущего и в результате окружность деформируется в спираль Фринеля . Если отверстия в экране бесконечно большие то амплитуда колебаний точки p будет определяться радиусом окружности.
Фринель предложил разбить поверхность волнового фронта на зоны( зоны Фринеля)
таким образом что расстояние до границ зоны от точки p отличается на
2
40
