
Konspekt_za_2y_semestr_po_fizike
.pdf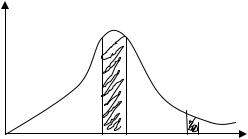
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
( * * ) |
|
|
(F *e ikR FiKeiKR FF *e iKR (k )) |
|||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
2mi |
|
|
|
|
|
2mi |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
k |
|
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
(K 2 * ) ( |
|
|
|
|
* ) (v * ) |
|||||||||||||
|
2mi |
m |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Полученное уравнение |
действительно совпадает с уравнение, где вместо |
||||||||||||||||||||||
* ( 2 )
Уравнение непрерывность выполняется для любой сохранённой величины где - плотность величины, а v-скорость её переноса.
Обычно в классической механике - это плотность заряда или вещества (материи). Такую же роль в квантовой механике должна играть ( )2
|
|
* * * |
|
|
|
|||
Если случайная величина x может принимать различные значения xi |
|
|||||||
Если |
в N опытах значение xi |
наблюдается N i раз |
то вероятность |
значения xi |
||||
называется Pi |
Limn |
Ni |
|
|
|
|
||
N |
|
|
|
|
|
|||
Очевидно pi 1 условие нормировки. |
|
|
|
|||||
|
i |
|
|
|
|
|
|
|
Среднем значением называется x Pi |
X i |
|
|
|||||
|
|
|
|
|
i |
|
|
|
Если |
есть |
функция f (xi ) то |
среднем |
значением |
этой функции |
называется |
||
f (x) pi f (xi )
i
Если имеются две независимые случайные величины, каждая из которых может принимать свои значения. xi Pi xn pn
Тогда совместная вероятность того, что первая величина принимает значение хi: а вторая при этом принимает значение xn
P Pi Pn
Если случайная величина х меняется непрерывно, то вероятностью того что x x dx (находится в интервале) W (x)dx W (x) -плотность вероятности.
Тогда условием нормировки
w(x)dx 1
Среднем значением функции
f f (x)w(x)dx
W
х1 х2 |
dx |
x |
61
|
|
x2 |
|
|
|
|
|
|
|
x1 x2 W (x)dx |
|
|
|
|
|
|
|
||
|
|
x1 |
|
|
|
|
|
|
|
*** |
|
|
|
|
|
|
|
||
Квадрат модуля волновой функции |
( )2 можно рассмотреть, как плотность |
||||||||
|
|
|
|
|
|
|
|
|
|
вероятность обнаружить частицу в |
интервале |
R |
|
R |
dR |
. Вероятность будет |
|||
|
|
|
|
|
|
|
|
|
|
( )2 dR |
( )2 dv |
|
|
|
|
|
|
|
|
Вследствие этого волновая функция обладает следующими свойствами: ( )2 dR 1 (
|
|
||
условие нормировки). Для выполнения , которого необходимо ( |
R |
) 0 |
R |
И волновая функция и её производные должны быть непрерывны. |
|
||
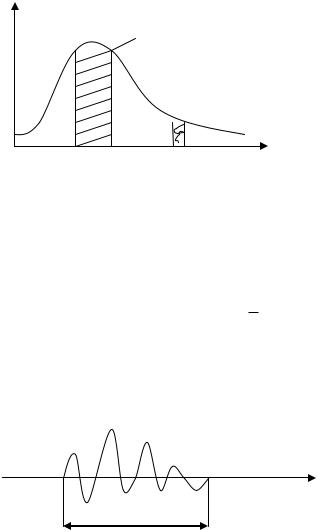
( )2
=1
R1 R2 |
dR |
R |
Вероятность что частицы находятся
|
R2 |
|
|
R1 R2 |
| |2 dR |
|
|
|
R1 |
||
|
|
§4 Принцип неопределенности Гейзенберга |
|
Рассмотрим одномерный случай, когда (R , t) (x, t)
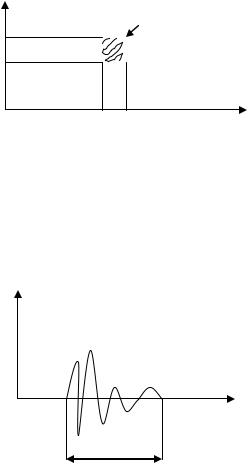
Если волновая функция частицы представляют собой волновой пакет протяжённостью
x
x
Таким образом очевидно вероятность обнаружения частиц будет отличаться от 0 только там где существует волновой пакет.
Таким образом о местоположение частицы можно говорить лишь с некоторой не определённостью x Для определения которой выполним § 2.9
x * K 2
62
x( k ) 2 |
|
||
x p 2 |
|
||
Где x не определённость координатами частицы, а |
p не определённость её |
||
импульсом. |
|
||
|
|
2 |
|
p |
|
|
|
|
|
|
|
x |
x |
Соотношение неопределенности Гейзенберга для координат и импульса.
Если мы точно знаем координаты частицы x 0 , то мы не знаем, как она двигается
p .
Если мы находимся в некоторой точке, и мимо нас пролетает частица, то есть мимо нас распространяется волновой пакет, то мы будем наблюдать импульс колебаний.
t
t
t длительность импульса определяет неопределенность времени, когда частица находится в данной точке пространства, то есть частица находилась в данной точке
пространства в течение t с разной вероятностью. В §1.7 было показано
t 2
t * ( ) 2t E 2
То есть если мы точно знаем время, то не знаем энергию.
§ 5 Движение частицы в поле с потенциальным барьером. Туннельный эффект.
Рассмотрим одномерный случай, когда положение частицы х. Пусть потенциальная энергия частицы имеет форму барьера.
63
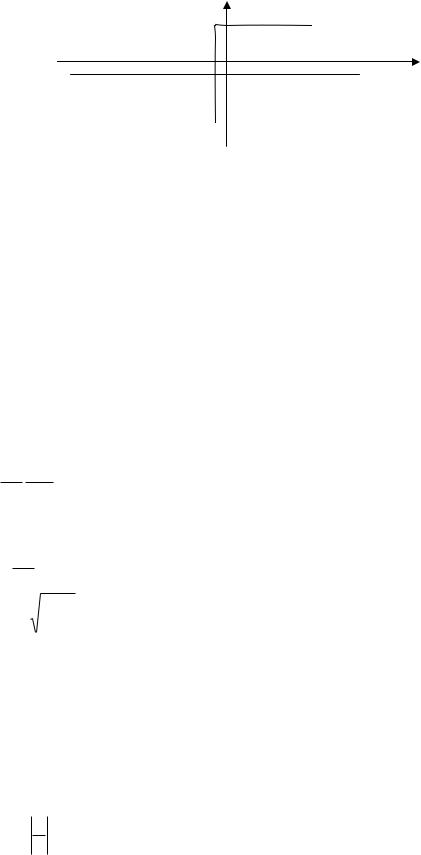
|
U(x) |
|
u0 |
u = 0 |
Fx 0 |
|
|
x<0 n=0 |
x > 0 u = u0 |
|
|
|
|
|
|
|
|
|
|
u |
Так как сила действующая на частицу F u F |
x |
|
||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотри частицу, полная энергия которой E u0 |
|
|
|
|||||||
Для определения волновой функции при заданной |
энергии E достаточно |
|||||||||
рассмотреть стационарное уравнение Шредингера, из которого находим (x) |
||||||||||
(x, t) (x)e i t |
|
E |
|
|
|
|
||||
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||
В одномерном случае |
|
|
|
|
|
|
||||
|
2 d 2 |
|
|
|
|
|
|
|||
|
|
|
|
(E u) 0 |
|
|
|
|
|
|
|
2m |
dx2 |
|
|
|
|
|
|
||
1) Рассмотрим x 0 |
u 0 |
|
|
|
||||||
2 d 2 E 0 2m dx2
Как известно решение этого уравнения будет иметь вид
(x) Ae ikx
2 k 2 Ae ikx EAe ikx 0 2m
K |
2mE |
||
|
|
||
|
2 |
||
|
|||
U общие решение
(x) Aeikx Be ikx
(x,t) (x)e i t Aei(kx t ) Bei( kx t )
Таким образом в полученном решение у нас будет 2-е волновые функции: вдоль Х («падающая волна») и волна против Х (отражённая волны)
| A |2 - определят плотность вероятности обнаружить частицу, которая двигается к потенциальному барьеру.
| B |2 плотность вероятности обнаружения отражённую частицу.
2
K BA -коэффициент отражения.
2) Рассмотри x>0
64

u u0 E
2 d 2 (E u0 ) 0 2m dx2
Решение уравнения имеет вид (x) Ce qx
q 2 2 (x) (E u0 ) (x) 0 2m
q |
|
2m(u0 E |
|
|
|
2 |
|
||
|
|
|
||
Тогда
(x) Ce qx De qx
Заметим, что решение eqx при x > 0 не подходит, так как оно не удовлетворяет условиям нормировки, поэтому
(x) Ce qx
Таким образом в области x>0 существует отличная от 0 волновая функция частиц и сумм вероятности обнаружить частицу за потенциальным барьером. Для того чтобы найти коэффициент отражения, запишем условие непрерывности волновой функции и её
производной в точке х = 0
A B C
d |
ikAeikx ikBe ikx |
|||||||||||||
|
|
|||||||||||||
dx |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
d |
qCe qx |
|
||||||||||||
|
|
|
||||||||||||
dx |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
ikA ikB qc |
|
|||||||||||||
ikA ikB q( A B) |
||||||||||||||
A |
ik q |
|
B |
|
||||||||||
ik q |
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||
K |
|
|
B |
|
|
2 |
|
ik q |
|
2 |
1 |
|||
|
|
|
|
|
|
|||||||||
|
|
|
||||||||||||
|
|
A |
|
ik q |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В области x<0 вероятность обнаружения падающую и отражённую одинакова. Так как решение найдено при E const по t
Туннельный эффект.
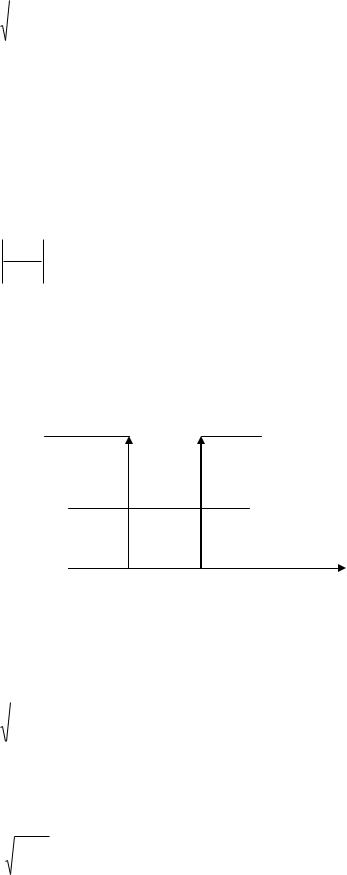
Рассмотри движение частицы в поле с потенциальным барьером вида
u |
|
|
Uo |
|
E |
|
||
n=0 |
|
u=0 |
|
|
|
|
|
|
0 a |
x |
|
Предположим, что частица находилась сначала в области x<0 , E u0 , тогда в области x<0 решением стационарного уравнения Шредингера будет иметь вид
65
(x) Aeikx Be ikx
0 x a
(x) Ce ax
q |
|
2m(u0 E) |
|
|
|
2 |
|
||
|
|
|
||
x 0
(x) Deikx
Таким образом существует вероятность, что частица может пройти потенциальный барьер и область x<0 в области x>a. Эта вероятность характеризуется коэффициентом пропускания, который равен квадрату модуля отношения (a)k (0)
T |
|
(a) |
|
2 |
|
|
(a) |
|
2 |
|
|
|
|
||||||
|
(0) |
|
|
|
(0) |
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
(x, t) (x)e i t
TCe qa 2 e 2qa
Ce qa
Таким образом если потенциальный барьер бесконечно широкой, то T 0 и если он бесконечно высок (q )
§6 Частица в потенциальной яме. Дискретность энергетического состояния.
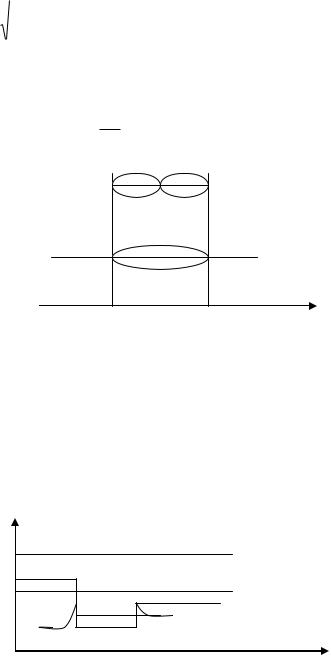
Рассмотрим частицу, которая находится в потенциальном поле имеющем форму ямы.
n |
u= |
E |
u 0 |
|
||
|
|
|
||
|
|
|
|
|
|
0 |
|
a |
x |
|
|
|
|
|
Как было показано в § 5 волновые функции частицы области u E
(x) ~ e qx
q |
|
2m(u E) |
|
||
|
|
|
|
||
2 |
|
|
|
||
|
|
|
|
|
|
Если u |
то q (x) 0 |
||||
Таким образом случай бесконечно глубокой ямы при x<0, x>a, (x) 0
Если 0<x<a то u 0
(x) Aeikx Be ikx
K |
2mE |
||
|
|
||
|
2 |
||
|
|||
66
Из левого граничного условия следует (0) 0 A B
BA
(x) A(eikx e kx ) C sin kx
Из второго граничного условия следует
(a) 0 |
|
|
sin ka 0 |
|||||
Ka n |
|
|
n 1,2,3... |
|||||
|
|
|
|
|
|
2 k 2 |
|
|
K |
|
2mE |
|
E |
|
|||
|
2 |
|
|
2m |
||||
|
|
|
|
|
||||
E |
2 |
2 |
|
n2 |
||||
|
|
|
2 |
|
||||
2m a |
|
|||||||
|
|
|
|
|
||||
Таким образом частица находится в потенциальной яме, то её энергетический спектр
дискретен. E En 2 2 n2
2m a 2
E1 |
n=1 |
|
x
Таким образом, частица которая находилась в потенциальной яме может принимать лишь дискретное значение энергии под действием постоянной скорость E не непрерывна.
Условие дискретности энергии спектр направление связано с характеристикой движения частиц. Если движение ограниченно, то спектр энергии дискретный.
Если движение частицы не ограниченно, то её энергетический спектр непрерывен.
u
E
x
E>u движение не ограниченно
67
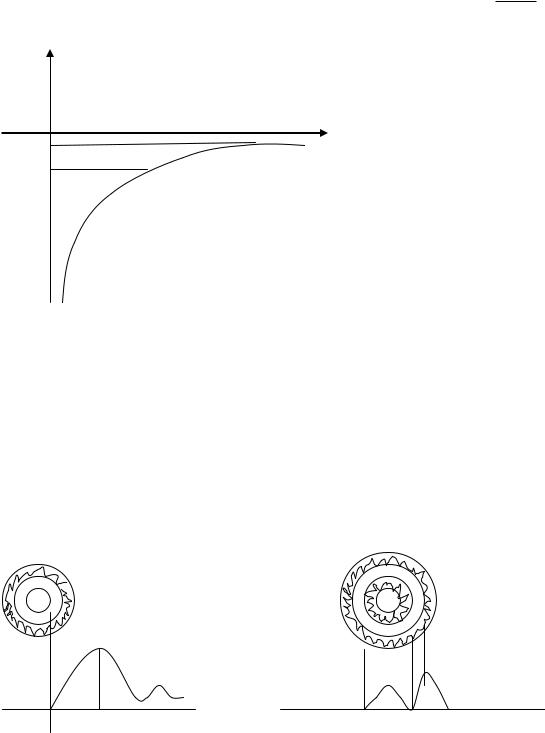
§7 Атом водорода.
Атом водорода состоит из тяжёлого ядра и лёгких электронов. Центр масс совпадает с
q2
центром ядра. Потенциальная энергия электрона в атоме водорода будет u e
4 e0 R
u
R
n=2
(R)
n=1 |
|
ER B1 6эB |
|
Если энергия электрона E<0 то такой электрон находится в потенциальной яме и его движение ограничено атомом водорода, Если E>0 то электрон выходит из потенциальной ямы, его движение становится неограниченным. Происходит ионизация атома водорода.
Рассмотрим сферически симметричный случай.
В этом случае энергия электрона будет принимать дискретное значение.
En |
|
ER |
n 1,2,3 |
||
n |
2 |
||||
|
|
|
|||
ER B1 6эB - Рибберг
n- главное квантовое число
В сферично симметричном случае волны функции имеют вид
n=1
+
| |2 | |2
В сферически симметрическом случае нельзя говорить о моменте импульса электрона, момент импульса равен 0.
Изменение энергии электрона можно лишь скачком (квантом)
Чтобы увеличения энергии должен получить квант от электромагнитного поля (поглотить фотон).
При уменьшения излучения квант энергии (фотоны)
68
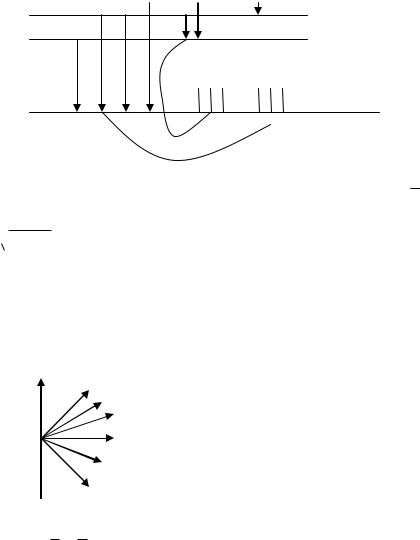
n=4 |
|
|
|
n=3 |
|
|
|
n=2 |
2 |
|
|
|
|
|
|
|
|
E |
|
|
1 |
||
n=1 |
|
|
|
|
|
1 2 |
|
Если волновая функция электрона сферична не симметрична (R ) , то электрон может иметь импульс
L 
 l(l 1)
l(l 1)
l орбитальное квантовое число. l 0,1,2…..(n-1)
Проекция момента импульса на произвольную ось z Lz m m- магнитно квантовое число
m l,...0,1,2...l
Z
L
Спин S 12 , 12
Каждое квантовое число влияет на энергетическое состояние и про этом спектры приобретают тонкую структуру.
69
n=4 |
l=0 |
|
l=1 |
|
l=2 |
|
l=3 |
|
|
|
|
|
|
|
|
n=3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=2
n=1
Наиболее вероятны переходы при которых l 1
§8 Принцип Паули. Периодическая таблица элементов.
Классическая механика две одинаковые частицы (два электрона) всегда можно различить, так как всегда можно проследить за движением каждой из них.
В квантовой механике не существует траекторий движения частиц (принцип неопределённости) поэтому проследить за движением каждой частицы, принципе невозможно в квантовой механике две частицы неразличимы. Рассмотрим две одинаковые частицы с волновой функции 1 ,2 и R1 , R1
1
R1 |
2 |
|
R2
1 (R1 ) 2 определить плотность вероятности обнаружить первую частицу в точке с координатами R1 .
Тоже самое для второй частицы в точке с координатами R2 , то совместно вероятно первая частица находиться в R1 , а вторая в точке R2 , должна быть равна произведению вероятностей. То есть общие функции двух частиц должна быть пропорциональна1 (R1 ) 2 (R2 ) . Поменяем частицы местами, тогда их общая волновой функции будет
1 (R2 ) 2 (R1 )
То есть общая волновая функция частиц измается, но так как частицы неразличимы то от перемены мест частиц их общая волновая функция измениться не должна. Таким образом, получим общую волновую функциональную частиц не удовлетворяющую принципу неразличимости частиц.
Для того чтобы выполнить оба условия для общей волновой функции .1) частица не различить, волна не меняется от перемены мест частиц.2) общая волновая функция зависит от произведения волновой функции.
70
