Konspekt_za_2y_semestr_po_fizike

R0

Легко заметить, что в первой зоне Фринеля сответсвует первая полуокружность спирали. Вторая зона Фринеля это вторая полуокружность спирали и тд.

Если отверстие в экране совместимо с размером первой зоны Фринеля то A1 2 A0 то есть в два раза больше чем без экрана, а энергия при этом будет больше в 4 раза.

Рассмотрим радиус n-й зоны Фринеля

Если R0

41

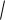R0 n

Рассмотрим случай когда точка наблюдения p находиться на очень большом расстояние от экрана с отверстием. 1 R0 будет очень большим и будет много

больше отверстия. То есть в отверстие экрана попадает малая часть первой зоны, поэтому амплитуда колебания в точке p будет небольшой. Если точка p будет приближаться к экрану (R0 уменьшиться) то радиус первой зоны Фринеля будет уменьшаться и в отверстие экрана будет попадать всё больше частиц, то есть А будет увеличиваться, максимальная амплитуда тогда когда радиус первой зоны совпадёт с размером отверстия.

A2

При дальнейшим приближение к экрану в отверстии будет помещаться вторая зона и амплитуда будет убывать.

Когда в отверстие экрана будет помещены обе зоны Фринеля А практически будет равна 0.

§2.9 Волновой пакет.

Рассмотрим 2-е монохроматические волны которые распространяться вдоль оси х с разной частотой и разным волновым вектором.

f (x1t) 2Acos( mt Km x) * cos( s t Ks x)

42

2AcosKmx t

x

В следующий момент времени вся картина сместиться вдоль оси х причём с разной скоростью будут перемещаться огибающий и наполняющий. Для определения скорости огибающей надо продифференцировать условие постоянства фаз.

Скорость наполняющей s . Эти скорости могут не совпадать.

K s

Рассмотрим большое количество монохроматических плоских волн с разной частотой и волновым вектором который растёт вдоль оси х

1 2 2 3 ...n 1 (N 1)

Пусть интервал между соседними волновыми числами тоже одинаков.

k K 2 K1 K3 K2

Это возможно в одном единственном случае, когда нет дисперсии, то есть фазовая

скорость v p const k

K

Тогда волновая функция будет f (x1t) Acos(1t k1 x) Acos(2t k2 x).... Повторяя выводы §1.7 находим.

43

2

Мы получим волновую функцию амплитуда которой зависит от времени и координаты sin t kx

f (x1t)

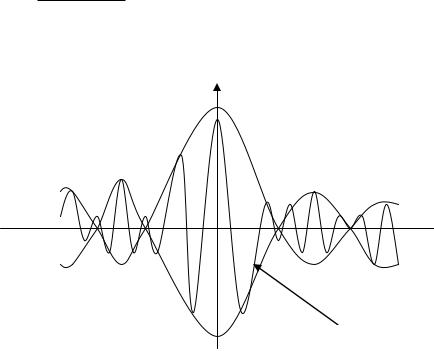
Таким образом при сложение большого числа монохроматических волн с различной частотой мы получим волновую функцию ограниченную в пространстве. Такая волновая функция называется волновым пакетом. За протяженность волнового пакета x выбирают половина расстояния между двумя ближайшими к максимуму нулями. x x1 Протяжённость волнового пакета x и интервал волновых чисел k образующие его монохроматические волны связанны между собой соотношением k x 2 .Следует

заметить что это равенство получено при определённых условиях .

В общем случае K * x 2 Таким образом мы получим, что в результате сложения большого числа монохроматических волн получается ограниченна в пространстве волновая функция. Справедливо и обратное утверждение. Любой произвольный волновой пакет можно представить в виде суммы гармонических волн.

f (x1t) A(k) cos( (k) y kx)dk

Где w(k) - дисперсионное соотношение.

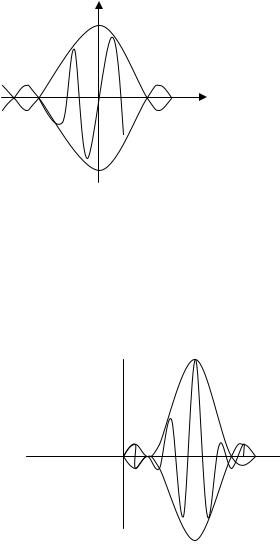
Рассмотрим поведение волнового пакета в следующие моменты времени.

44

t

x

t t 0 все складываемые волны функции сместятся вдоль оси х на одинаковом расстояние так как в отсутствие дисперсии фазовые скорости все одинаковы.

В результате сумма всех волновых функции тоже сместиться на такое же расстояние. Скорость перемещения волнового пакета будет совпадать с фазовой скоростью волны.

При этом очевидно, что форма волнового пакета изменяться не будет.

Если фазовые скорости будут различны для разных волн(есть дисперсия) то волновой пакет будет деформироваться при распределении и скорость его движения будет отлична от фазовой скорости.

§ 2.10 Групповая скорость. Метод стационарных фаз

В§ 2.9 было показано, что любую произвольную волновую функцию можно предоставить в виде суммы гармонических волн.

(k) (k)t kx - фаза гармонической волны.

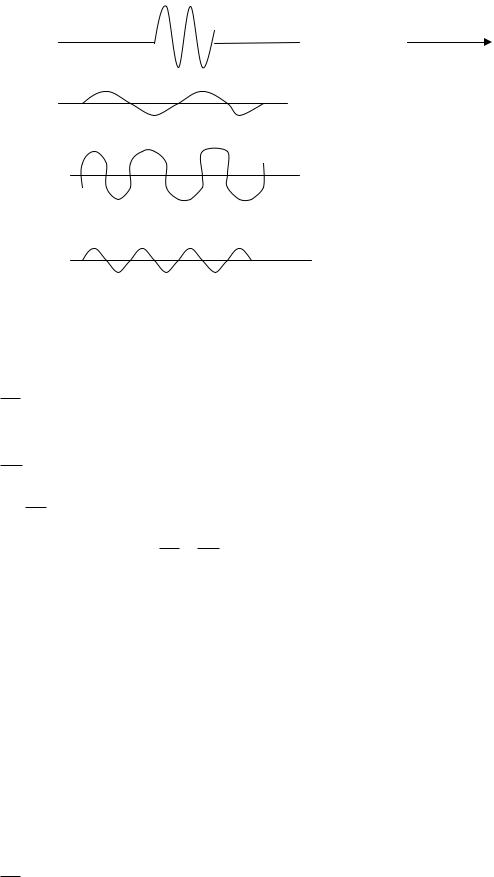
Заметим, что вычисления интеграла в общем виде является очень сложной задачей

45

x

v p1

v p 2

v p3

Замети, что при сложение гармонических функций результат будет заметно отличаться от 0 только если фазы гармонических функций будут близкими. В остальных случаях результат будет близким к нулю, то есть условие того что полученный интеграл не равен 0 совпадает с условием одинаковых фаз складываемых волн, то есть с условием постоянства фаз для различных k

d 0 dk

(k)t kx

d t x 0 dk

x dwdk t - полученный интеграл будет отличаться от 0

Другими словами Vg dw d dk dk

Vg- групповая скорость w(k)

Vg- скорость распространения волнового пакета.

Vp k

Vp K

Если фазовая скорость (Vp) не зависит от k (нет дисперсии) то групповая скорость совпадает с фазовой. В противном случае групповая скорость будет отличаться от фазовой.

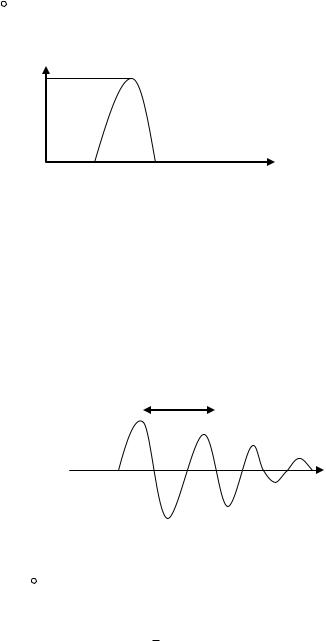
Таким образом рассмотреваемый интеграл будет отличаться от 0 лишь в небольшой области K для которой фаза волны (k) примерно одинаково.

Для того чтобы найти это значение K надо решить уравнение..

dwdk t x 0 - относительно K из которого найдём k0 k(x1t) Тогда интеграл можно записать в виде.

46

f (x1t) 2eA(K0 ) cos (K0 ) 2eA(k(x1t))cos (k(x,t)) A(x,t) cos w(k(x,t))*t k(x,t)xA(x,t) cos( (x,t)t k(x,t)x)

Любой произвольный волновой пакет можно записать в том же виде что и монохроматическую волну с той лишь разницей, что амплитуда, частота и волновой вектор зависит от координат и времени.

x

Для (x,t) A(x,t) cos (x,t) можно ввести понятие k . Частот произвольной

волновой функцией называется , а K

Втрёхмерном случае k

§2.11 Пространственная и временная когерентность. Поляризация.

В§2.4 было показано что условие максимума интерференции двух источников сводится к тому что геометрическая разность хода S d sin m

d- расстояние между источникам .

47

d sin (m 1)

d sin (m )

d

Угловое расстояние между двумя ближайшими максимумами

2

d(sin 2 sin 1 )

Для малых углов d ( 2 1 ) x

d

Если источник излучения волны с различной длинной волны, то положение максимума порядка m будет размыто d sin m

Условием максимума для разных длин будет выполнен для разных условий. Если источник излучения волны в интервале 2 1 . При малых углах .

d m d m

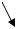
m

Для того чтобы картина интерференции наблюдалась необходимо

m

d d

m

S m 2

48

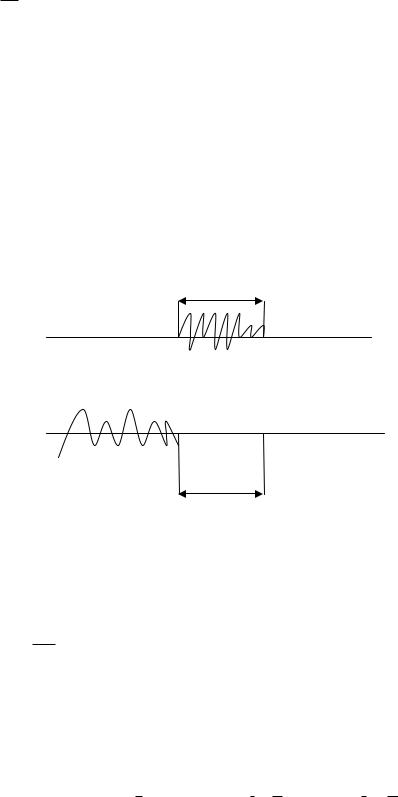
длина когерентности.

Для того чтобы наблюдать интерференционную картину необходимо чтобы разность хода была меньше длины когерентности.

Выясним, что представляет собой длина когерентности.

В §2.9 было показано, что размер волнового пакета удовлетворяет соотношению.

Длина когерентности совпадает с длиной волнового пакета

x

S

Если два источника излучают волновые пакеты, то в точке наблюдения p мы будем регистрировать импульсы колебаний.

Если время регистрации будет меньше длительности импульса, то колебания будут

складываться. Длительность колебаний называется длительностью когерентности.

t 2

t 2

Таким образом если время в течение которого происходит регестрация. волновой функции меньше времени когерентности, а расстояние на котором наблюдается волновая функция меньше длины когерентности. То источник этой волновой функции называется когерентным.

Волновая функция, как правило описывает физические величины и также как и они может быть скалярной и векторной.

Если волновая функция векторная, то существует три класса волны: поперечные( волновая функции k ) продольная ( f || K ) и косая ( f K )

В случае поперечных волн вводят понятие поляризации волны. Это понятие характеризует поведение вектора волновой функции f .

Если при распространение волны вектор волновой функции всё время остаётся в одной плоскости то говорят что волна плоско или линейно поляризована .Если при распространение волны величина волнового вектора постоянна, а направление меняется по кругу, то говорят о круговой поляризации волны.

49

Если при этом ещё и меняется величина волнового вектора, то говорят об элетрической поляризации.

Следует заметить, что при таковой классификации любая поперечная волна будет поляризована.

Реальные источники волны обычно излучают волновые пакеты, каждый из которых поляризован по-своему.

Если время регистрации (наблюдения) будет больше времени когерентности, то поляризация каждого волнового пакета определить не удастся и в этом случае говорят о естественной или неполяризованной волне. Тоже самое будет если расстояние на котором наблюдаются волны больше длины когерентности.

§2.12 Приближение геометрической оптики. Уравнение Эйконала. Принцип Ферма.

В §2.10 было показано, что любую произвольную волновую функцию можно записать

ввиде.

поверхностью или волновым фронтом. В общем случае это произвольная поверхность. Разобьём эту поверхность на участки, такие, что их можно считать плоскими.

Если при этом размере участка будет много больше длинны волны, а время в течение которого этот участок остаётся плоским много больше периода волны, то можно говорить о приближение геометрической оптики рассмотрим один такой участок для начало систем координат поместим на этом участке и за начало отсчёта времени выберем

0

Разложим фазу колебаний в степенной ряд в окружности точки R 0 t = 0

этого следует что в приближение геометрической оптики при разложение в ряд фазы можно ограничить лишь первыми членами ряда

(R , t) (0) t KR

Вэтом приближение можно считать, что направление распространения произвольной волны совпадает с направление K в каждой точке волнового фронта как в плоской волне,

50